Содержание
- 2. Гармоническим осциллято- ром называется частица, со- вершающая гармонические колебания. Потенциальная энергия равна (11.1) поэтому уравнение Шредингера
- 3. Качественно задача подобна рассмотренной вы-ше задаче о движении частицы в потенциаль-ной яме, однако здесь имеется особенность,
- 4. Будем искать решение в виде (11.5) Тогда для функции v получаем следующее уравнение: (11.6) Будем искать
- 5. Подставим (11.7) в (11.6): Приравнивая нулю сумму коэффициентов при оди- наковых степенях, получаем следующие рекуррен- тные
- 6. Отсюда и из формулы (11.3) находим энергию ос-циллятора: (11.10) в частности, при n = 0 минимальная
- 7. Рекуррентная формула (11.8) позволяет последо-вательно вычислить все члены ряда. Функцию v можно теперь записать в виде:
- 9. Скачать презентацию






 Доходы бюджетов
Доходы бюджетов мониторы
мониторы Презентация на тему "Родительская любовь и Воспитание" - скачать презентации по Педагогике
Презентация на тему "Родительская любовь и Воспитание" - скачать презентации по Педагогике Одежда 15-16 веков
Одежда 15-16 веков Старинная русская одежда. (4 класс)
Старинная русская одежда. (4 класс) Расчет строительных конструкций
Расчет строительных конструкций Презентация Роль профсоюзов на рынке труда
Презентация Роль профсоюзов на рынке труда О весенней охоте
О весенней охоте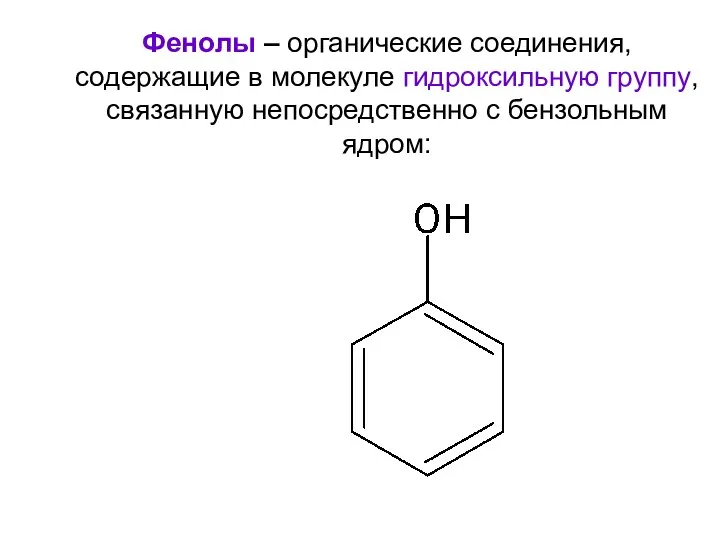 Фенолы
Фенолы Нарушения обмена белков и нуклеиновых кислот
Нарушения обмена белков и нуклеиновых кислот Алкоголь и алкогольная зависимость
Алкоголь и алкогольная зависимость Презентация "Фонтаны Томска"
Презентация "Фонтаны Томска" День матери 2017
День матери 2017 О святости
О святости Клод Моне
Клод Моне Инфекционный мононуклеоз
Инфекционный мононуклеоз Устройство компьютера
Устройство компьютера  Алгоритмы и структуры данных на Python
Алгоритмы и структуры данных на Python Семейный клуб «РОДНИЧОК» 1 КЛАСС Классный руководитель – Чачина Людмила Васильевна
Семейный клуб «РОДНИЧОК» 1 КЛАСС Классный руководитель – Чачина Людмила Васильевна Снеговик спешит на карнавал - презентация для начальной школы_
Снеговик спешит на карнавал - презентация для начальной школы_ исИстория органов внутренних дел Российской Федерации.тория
исИстория органов внутренних дел Российской Федерации.тория Условный оператор. Конструкция if
Условный оператор. Конструкция if Экипаж «IT Empire»
Экипаж «IT Empire» Двигатели «Камминз». Диагностика неисправностей
Двигатели «Камминз». Диагностика неисправностей Органы исполнительной власти в РФ
Органы исполнительной власти в РФ ИТ-архитектура предприятия. Применение модели Захмана для решения проблем, возникающих на этапе реализации IT-проекта
ИТ-архитектура предприятия. Применение модели Захмана для решения проблем, возникающих на этапе реализации IT-проекта Культура Средневековой Индии
Культура Средневековой Индии Проект Продвижение комплекса ГТО среди сверстников. Мариинский муниципальный район
Проект Продвижение комплекса ГТО среди сверстников. Мариинский муниципальный район