Содержание
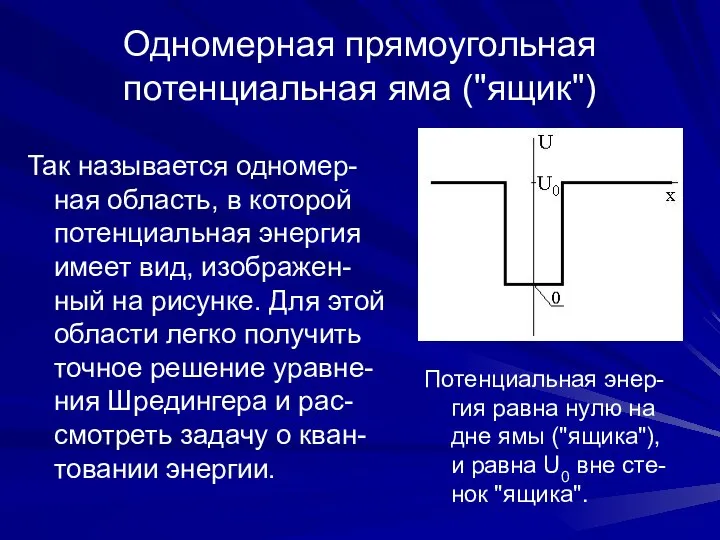
- 2. Одномерная прямоугольная потенциальная яма ("ящик") Так называется одномер-ная область, в которой потенциальная энергия имеет вид, изображен-ный
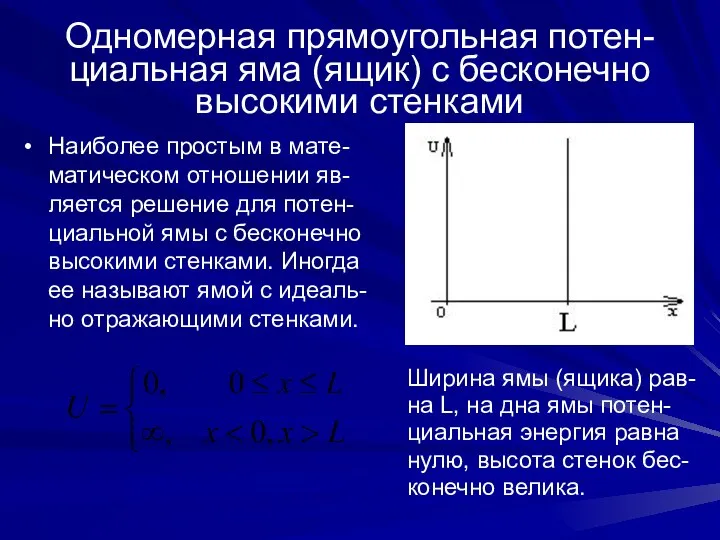
- 3. Одномерная прямоугольная потен-циальная яма (ящик) с бесконечно высокими стенками Наиболее простым в мате-матическом отношении яв-ляется решение
- 4. В этом случае внутри ямы частица дви-жется свободно, но выйти за ее преде-лы не может, т.е.
- 5. Стационарное уравнение Шредингера (8.6) внутри ямы принимает вид (т.к. U = 0): (9.2) Общее решение этого
- 6. Из условия (9.1) Ψ(0) =0 следует, что B = 0. Из второго граничного условия Ψ(L) =0
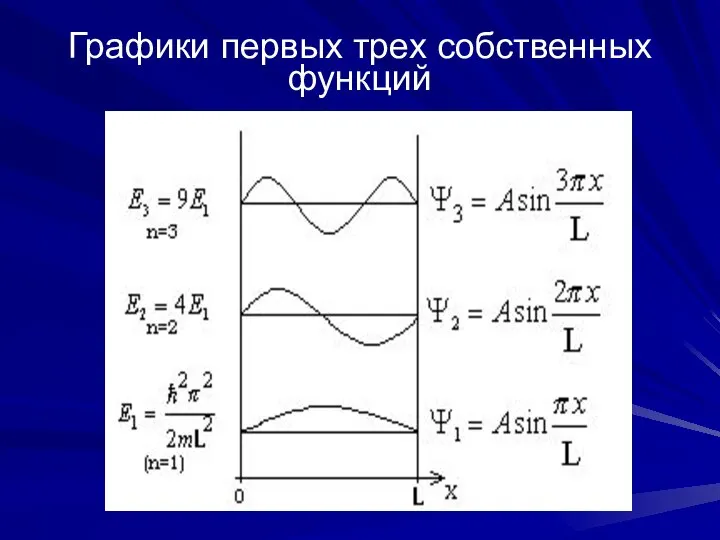
- 7. Таким образом, собственными функция-ми уравнения Шредингера в рассматри-ваемой задаче являются волновые функции вида (9.5) Собственные значения
- 8. Таким образом, частица (например, электрон) в потенци-альной яме может иметь не произвольные, а лишь дис-кретные, квантованные
- 9. Если m = n, то интеграл (9.7) не равен 0, и из условия нормировки можно найти
- 10. Графики первых трех собственных функций
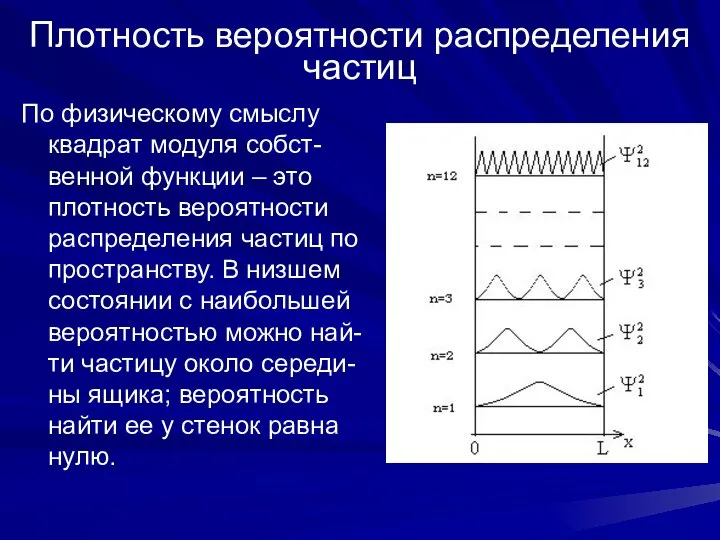
- 11. Плотность вероятности распределения частиц По физическому смыслу квадрат модуля собст-венной функции – это плотность вероятности распределения
- 12. Этот результат резко отличается от клас-сического: в классической механике на-хождение частицы в ящике с зеркаль-ными стенками
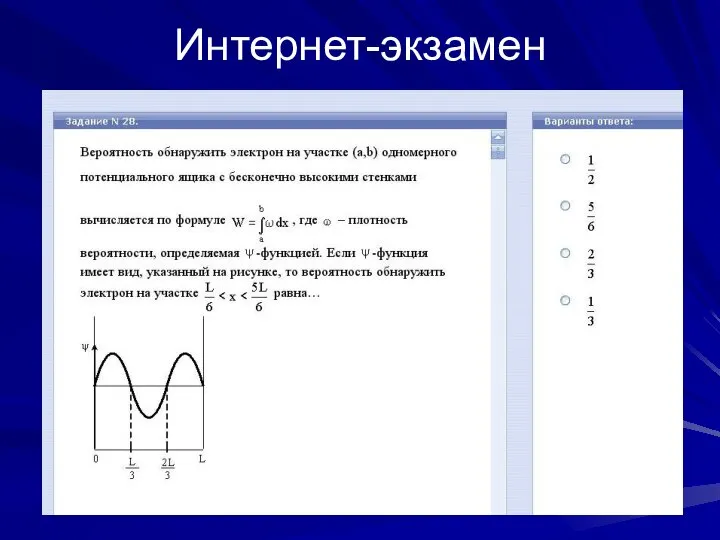
- 13. Интернет-экзамен
- 15. Скачать презентацию







 СССР в 30-е годы Индустриализация, коллективизация, внешняя политика
СССР в 30-е годы Индустриализация, коллективизация, внешняя политика Локомотивтің механикалық бөлігінің динамикалық сапа көрсеткіштері
Локомотивтің механикалық бөлігінің динамикалық сапа көрсеткіштері Продвижение ВФСК ГТО среди сверстников
Продвижение ВФСК ГТО среди сверстников Правила этики оценщиков
Правила этики оценщиков Исполнительные органы общества
Исполнительные органы общества Единый орфографический режим 2011-2012 учебный год
Единый орфографический режим 2011-2012 учебный год Задачи НПО
Задачи НПО  Операційні системи. Виклик віддалених процедур Remote Procedure Call (RPC)
Операційні системи. Виклик віддалених процедур Remote Procedure Call (RPC) Писанки в різних регіонах України
Писанки в різних регіонах України Образ птицы в народном искусстве
Образ птицы в народном искусстве КГМУ Кафедра общей хирургии Особенности обследования хирургического больного
КГМУ Кафедра общей хирургии Особенности обследования хирургического больного  Рекуррентные оптимальные алгоритмы фильтрации случайных процессов. Фильтр Калмана-Бьюси
Рекуррентные оптимальные алгоритмы фильтрации случайных процессов. Фильтр Калмана-Бьюси Тестовые задания. Конструкция, эксплуатация и техническое обслуживание автомобилей
Тестовые задания. Конструкция, эксплуатация и техническое обслуживание автомобилей pro_knigi
pro_knigi Семинар-тренинг «Стратегический маркетинг для СМБ» Автор, ведущий: Калинин Сергей Иванович
Семинар-тренинг «Стратегический маркетинг для СМБ» Автор, ведущий: Калинин Сергей Иванович  Обработка событий в JavaScript. Лекция № 9
Обработка событий в JavaScript. Лекция № 9 Алфавит. Таблица звуко-буквенных обозначений (продолжение)
Алфавит. Таблица звуко-буквенных обозначений (продолжение) Стандарт DSA - Digital Signature Algorithm
Стандарт DSA - Digital Signature Algorithm Регистрация результатов обучения учащихся при внедрении системы критериального оценивания
Регистрация результатов обучения учащихся при внедрении системы критериального оценивания Театры и музеи Москвы
Театры и музеи Москвы Основы электричества и электротехники. Часть I
Основы электричества и электротехники. Часть I Телекомунікаційне обладнання для підключення до транспортної мережі
Телекомунікаційне обладнання для підключення до транспортної мережі Методи аналізу ризику та надійності АЕС. Лабораторна робота №2
Методи аналізу ризику та надійності АЕС. Лабораторна робота №2 ЛЕКЦИЯ №9 РЯДЫ ДИНАМИКИ Ч.1
ЛЕКЦИЯ №9 РЯДЫ ДИНАМИКИ Ч.1  Презентация на тему "Модернизация высшего профессионального образования в России" - скачать презентации по Педагогике
Презентация на тему "Модернизация высшего профессионального образования в России" - скачать презентации по Педагогике Мұнайды гидроөңдеу процестері. Катализаторлары
Мұнайды гидроөңдеу процестері. Катализаторлары Решение задач с величинами: цена, количество, стоимость - презентация для начальной школы_
Решение задач с величинами: цена, количество, стоимость - презентация для начальной школы_ Географические объекты в русском песенном творчестве
Географические объекты в русском песенном творчестве