Содержание
- 2. CONTENTS Query languages in DB Properties of binary operations Relational algebra operations Examples Equivalent transformation and
- 3. Query languages Language categories: procedural (HOW to receive) nonprocedural (WHAT to receive) Formal languages: relational algebra
- 4. Relational algebra closure and properties of binary operations Algebra = data (of the defined type) +
- 5. Relational algebra operations Basic operations: set-theoretic (union, intersection, difference) projection selection cartesian product, join division Additional
- 6. Set-theoretic operations Two relations R and S are (union) compatible if: R and S have the
- 7. Union operation Union of two compatible relations R and S with schemas R(A) and S(A), where
- 8. Difference operation Difference of two compatible relations R and S with schemas R(A) and S(A), where
- 9. Intersection operation Intersection of two compatible relations R and S with schemas R(A) and S(A), where
- 10. Projection operation Projection of the relation R with schema R(A), where A is a set of
- 11. θ-comparability of attributes and tuples Let’s θ is any of the following comparison operators : =,
- 12. Selection (restriction) operation Let’s М and N are sets of θ-comparable attributes of the relation R
- 13. Cartesian product Cartesian product of two rations R and S with schemas R(А) and S(B) (A
- 14. Join operation Let us M and N are sets of θ-comparable attributes. Join of the relations
- 15. Join and natural join Join on a condition of equality (=) is called as equi-join .
- 16. Semijoin Semijoin is join of two relations with deleting from the resulting relation attributes of one
- 17. Image of the tuple Image of the relation R(M,N) with respect the tuple t1 ∈ R[M],
- 18. Division operation (1) Division of two relations R(M,N) and S(K,L) with respect of set of compatible
- 19. Division operation(2) Example: R S S[C] R[C÷C]S Division operation is expressed by other operations of RA:
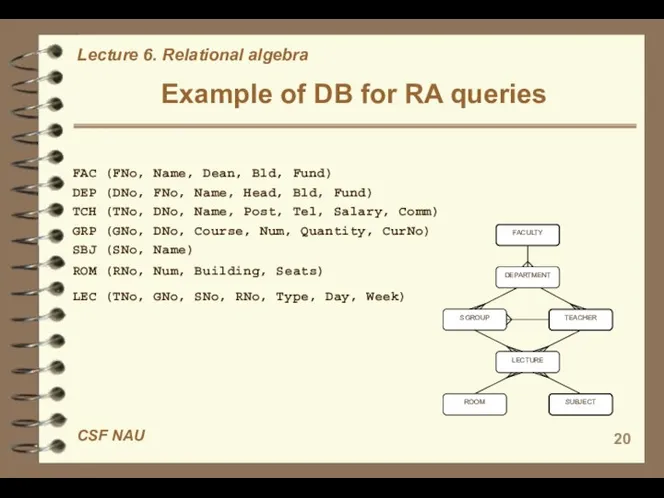
- 20. FAC (FNo, Name, Dean, Bld, Fund) DEP (DNo, FNo, Name, Head, Bld, Fund) TCH (TNo, DNo,
- 21. Examples of queries in RA (1) Projection: Output list jf teacher names and posts: TCH[Name, Post]
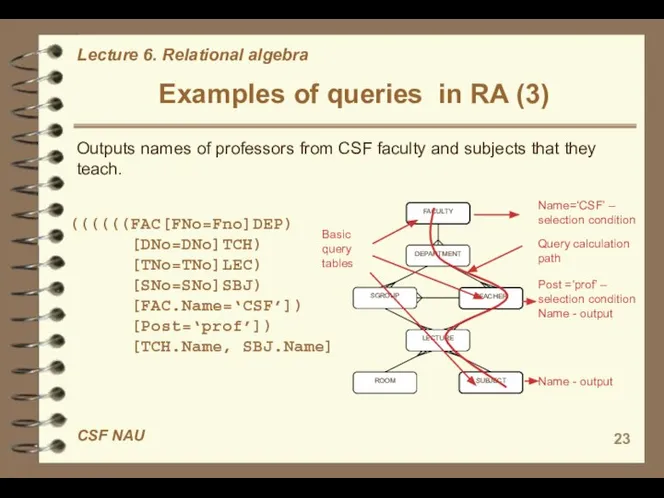
- 22. Examples of queries in RA (2) Composition of join, selection and projection 1) Outputs names of
- 23. Examples of queries in RA (3) Basic query tables Name=‘CSF’ – selection condition Query calculation path
- 24. Examples of division operation 1) Output teacher numbers that teach in ALL groups: ((LEC[TNo,GNo])[GNo÷GNo]GRP)[TNo] 2) Output
- 25. Additional operations Additional operations Assignment Renaming Generalized projection Outer join …
- 26. Assignment operation The assignment operation (←) provides a convenient way to express complex queries, write query
- 27. Rename operation The rename operation allows us to name, and therefore to refer to, the results
- 28. Generalized projection operation Extends the projection operation by allowing arithmetic functions to be used in the
- 29. Outer join Outer join is an extension of the join operation that avoids loss of information.
- 30. Outer join – example of ordinary join 1) Ordinary join (inner join) FAC [Fno=Fno] DEP FAC
- 31. Left outer join FAC FNo Name Dean F-1 CSF Ann F-2 CTF Dick F-3 CEF Bob
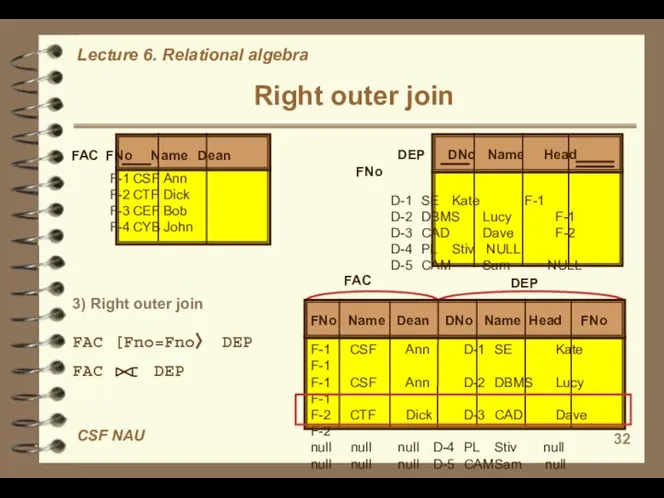
- 32. Right outer join FAC FNo Name Dean F-1 CSF Ann F-2 CTF Dick F-3 CEF Bob
- 33. Full outer join 4) Full outer join FAC 〈Fno=Fno〉 DEP FAC DEP FNo Name Dean DNo
- 34. Equivalent transformations of relational expressions 1) Commutativity of selection: σF(σG(R))=σG(σF(R))=σF&G(R) 2) Commutativity of selection and projection:
- 35. Optimization of RA expressions R(A,B) S(C,D) R(A,B) S(C,D) RA,B) S(C,D) R(A,B) S(C,D) × × × σD=9
- 36. General rules of RA expressions optimization General rules of RA expressions optimization: Transform each selection σF1&...&Fn(E)
- 38. Скачать презентацию

















![Division operation(2) Example: R S S[C] R[C÷C]S Division operation is expressed](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1293820/slide-18.jpg)














 Урок МХК Культурное влияние Византии и формирование русского национального стиля. Учитель МОУ СОШ № 4 Туркменского района Адонь
Урок МХК Культурное влияние Византии и формирование русского национального стиля. Учитель МОУ СОШ № 4 Туркменского района Адонь Основы алгоритмизации
Основы алгоритмизации Региональные компьютерные сети
Региональные компьютерные сети 1019109
1019109 Строение ядра
Строение ядра Техническое обучение по харвестерной головке Лог Макс 6000
Техническое обучение по харвестерной головке Лог Макс 6000 Устройство стиральной машины LG. Электрика
Устройство стиральной машины LG. Электрика забавная астрономия - презентация для начальной школы
забавная астрономия - презентация для начальной школы Нормативная база ГМО
Нормативная база ГМО Обязанности человека и гражданина РФ
Обязанности человека и гражданина РФ  Античная росписная керамика
Античная росписная керамика Иррациональные уравнения «Урок-дискуссия»
Иррациональные уравнения «Урок-дискуссия»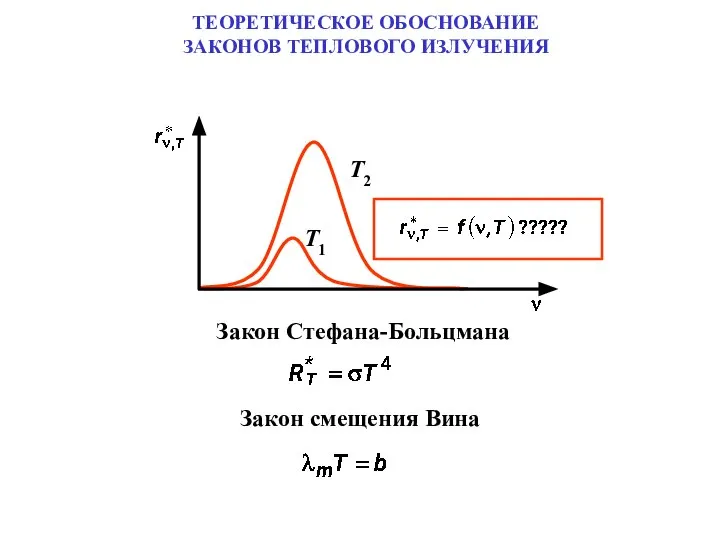 ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ ЗАКОНОВ ТЕПЛОВОГО ИЗЛУЧЕНИЯ
ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ ЗАКОНОВ ТЕПЛОВОГО ИЗЛУЧЕНИЯ Проектирование и технология ЭКБ
Проектирование и технология ЭКБ Виды принтеров
Виды принтеров Новая конституция РФ (часть 4)
Новая конституция РФ (часть 4) Естественное вскармливание
Естественное вскармливание Русская культура XVII в
Русская культура XVII в Презентация на тему "Туберкулез -Чума ХХІ века" - скачать презентации по Медицине
Презентация на тему "Туберкулез -Чума ХХІ века" - скачать презентации по Медицине Презентация на тему "Объяснительная записка" - скачать презентации по Педагогике
Презентация на тему "Объяснительная записка" - скачать презентации по Педагогике Источники доказательств
Источники доказательств Менің сыныптағы заттарым. Менің бөлмемдегі заттарым
Менің сыныптағы заттарым. Менің бөлмемдегі заттарым Презентация на тему "Правильное питание в современном мире" - скачать презентации по Медицине
Презентация на тему "Правильное питание в современном мире" - скачать презентации по Медицине Государство и его сущность
Государство и его сущность Основные этапы становления и развития статистической науки
Основные этапы становления и развития статистической науки Droga krzyżowa dziecka nienarodzonego
Droga krzyżowa dziecka nienarodzonego иерсинии
иерсинии Алгоритмы и программирование
Алгоритмы и программирование