Содержание
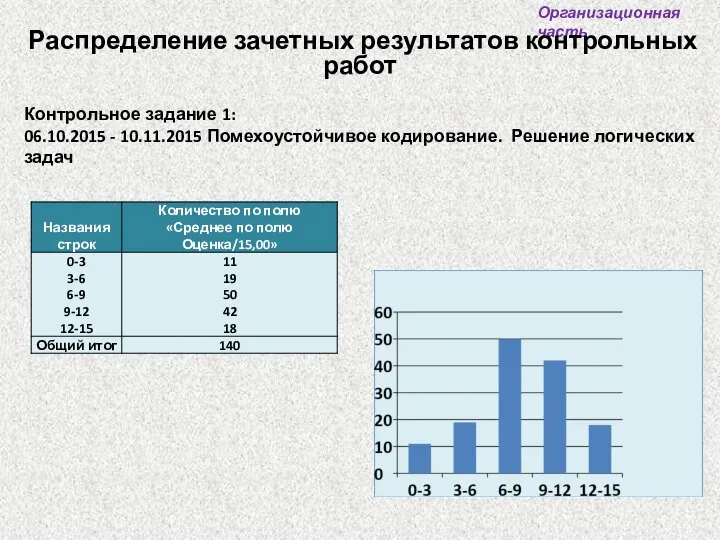
- 2. Контрольное задание 1: 06.10.2015 - 10.11.2015 Помехоустойчивое кодирование. Решение логических задач Организационная часть Распределение зачетных результатов
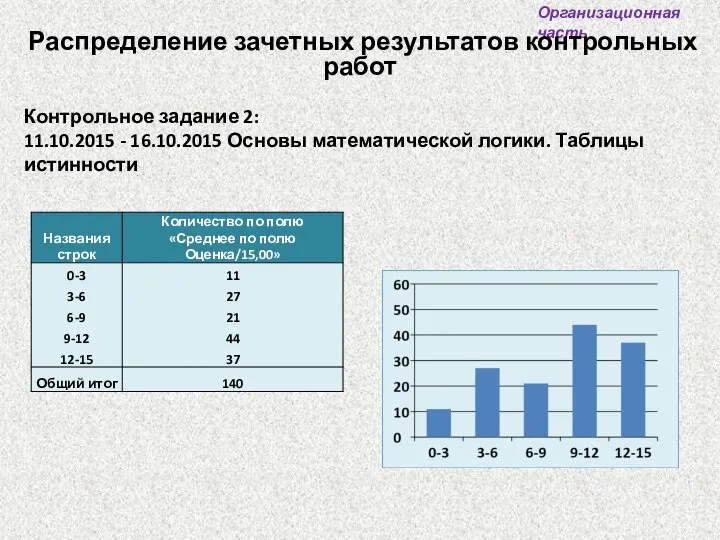
- 3. Контрольное задание 2: 11.10.2015 - 16.10.2015 Основы математической логики. Таблицы истинности Организационная часть Распределение зачетных результатов
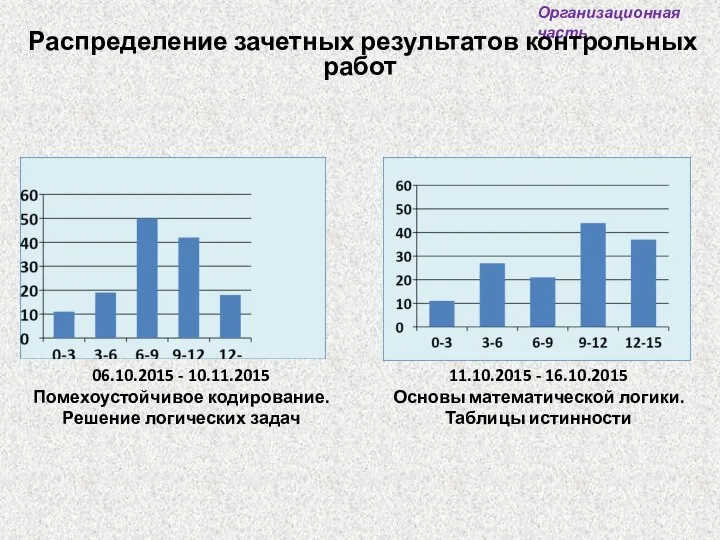
- 4. 11.10.2015 - 16.10.2015 Основы математической логики. Таблицы истинности 06.10.2015 - 10.11.2015 Помехоустойчивое кодирование. Решение логических задач
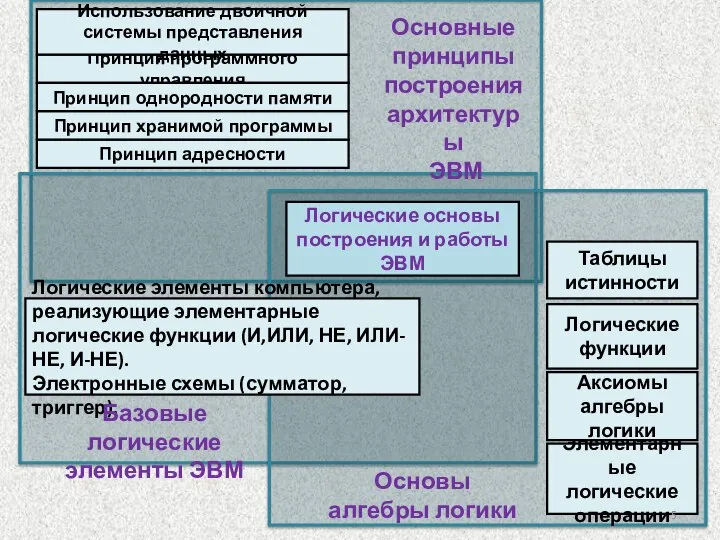
- 5. Таблицы истинности Логические основы построения и работы ЭВМ Принцип программного управления Логические элементы компьютера, реализующие элементарные
- 6. Логические операции «И», «ИЛИ», «НЕ» лежат в основе работы преобразователей информации любого компьютера. Клод Шеннон впервые
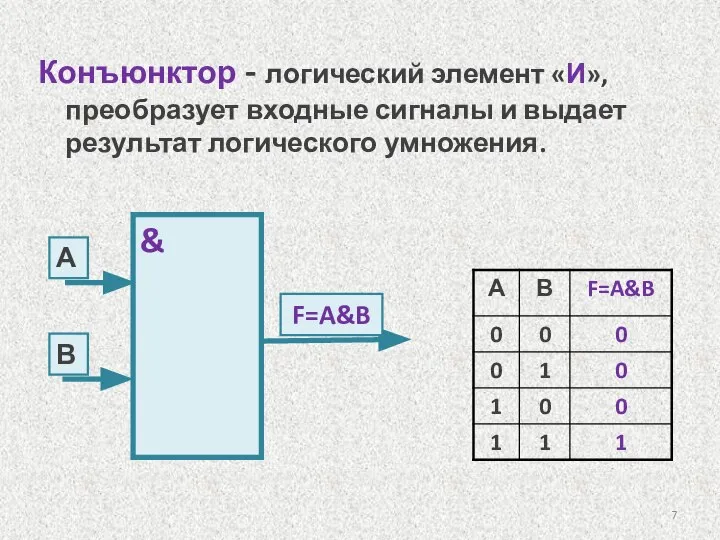
- 7. Конъюнктор - логический элемент «И», преобразует входные сигналы и выдает результат логического умножения. & А F=A&B
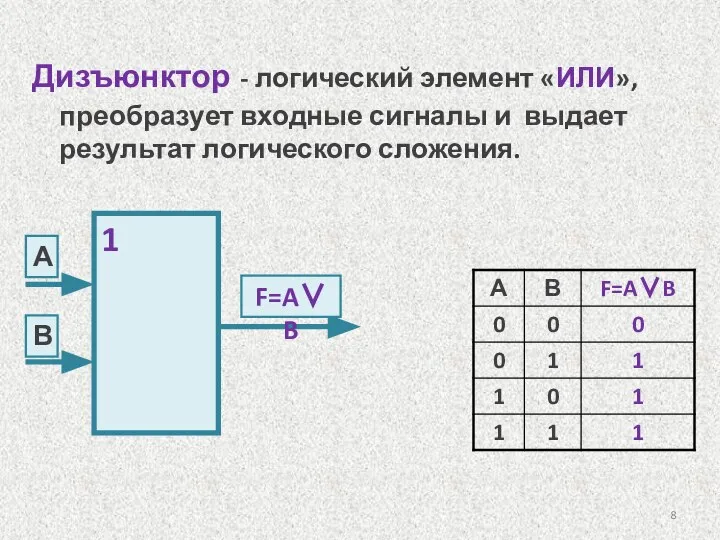
- 8. Дизъюнктор - логический элемент «ИЛИ», преобразует входные сигналы и выдает результат логического сложения. 1 А F=A∨B
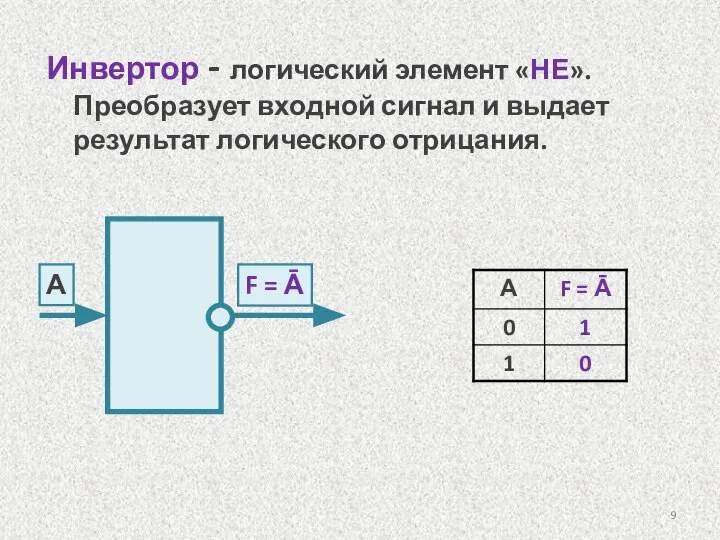
- 9. Инвертор - логический элемент «НЕ». Преобразует входной сигнал и выдает результат логического отрицания. А F =
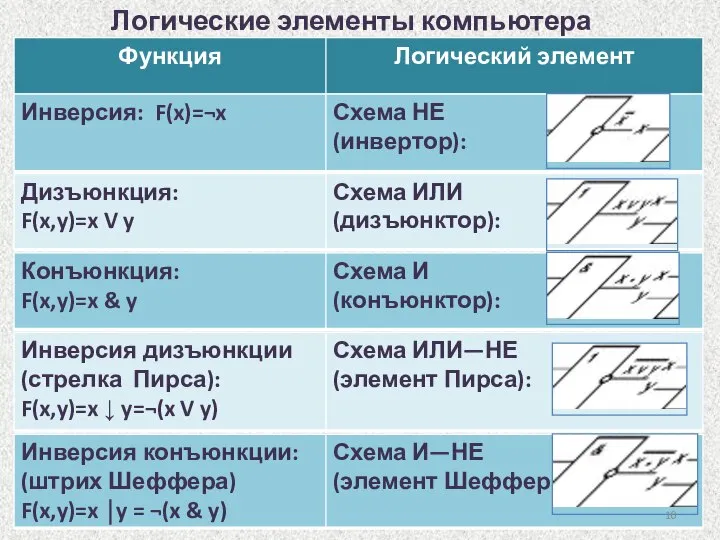
- 10. Логические элементы компьютера
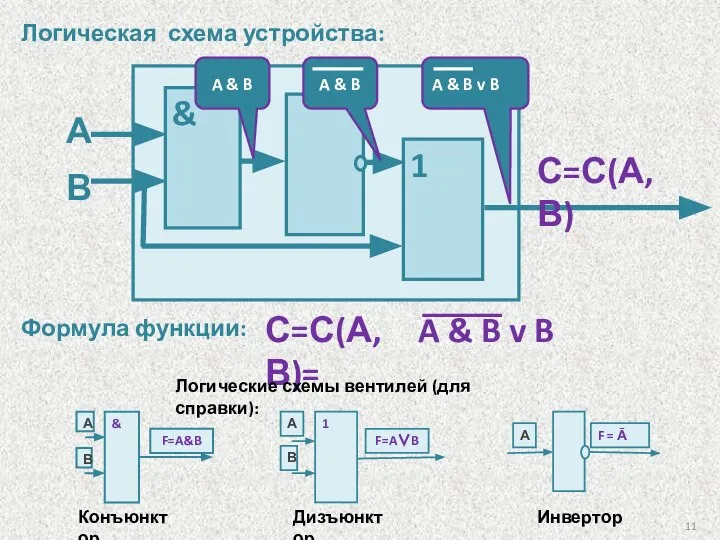
- 11. Логическая схема устройства: Формула функции: & А В 1 С=С(А,В)= A & B A & B
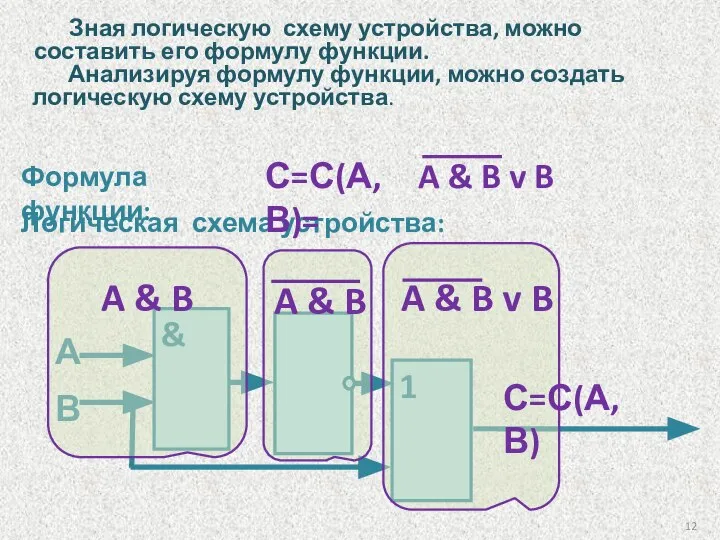
- 12. Логическая схема устройства: Формула функции: & А В 1 Анализируя формулу функции, можно создать логическую схему
- 13. Канонические формы булевых функций Элементарной конъюнкцией называется конъюнкция нескольких переменных и/или их инверсий, причем среди переменных
- 14. Совершенной дизъюнктивной нормальной формой (СДНФ) функции F (x1, x2, … , xn) называется ДНФ, равная 1
- 15. СДНФ функции F (x1, x2, … , xn) можно получить - с помощью равносильных преобразований, -
- 16. Получение СДНФ функции с помощью равносильных преобразований Для формулы функции получить ДНФ. Затем помощью равносильных преобразований
- 17. Переход от таблицы истинности функции к СДНФ Правило перехода от таблицы истинности к формуле функции в
- 18. Пример 1. Задана таблица истинности булевой функции F(X, Y, Z). Составить СДНФ и логическую схему функции
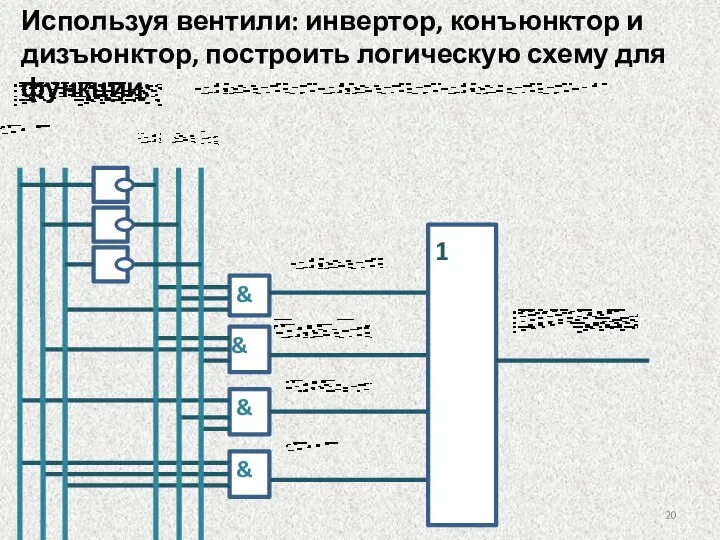
- 20. Используя вентили: инвертор, конъюнктор и дизъюнктор, построить логическую схему для функции:
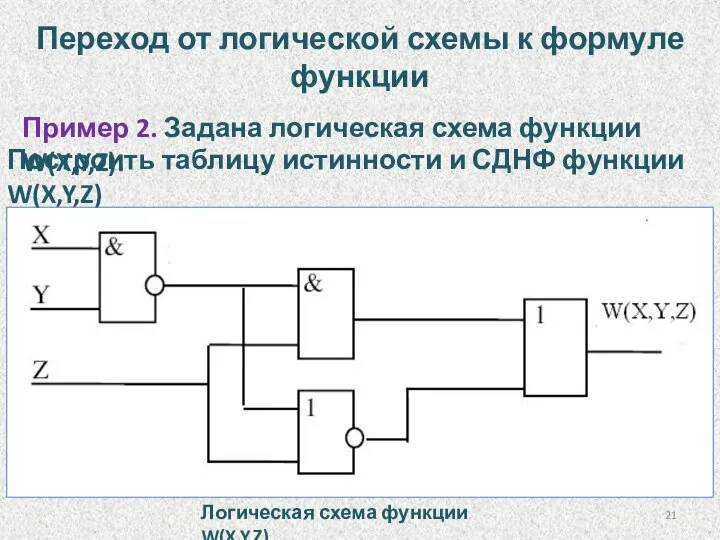
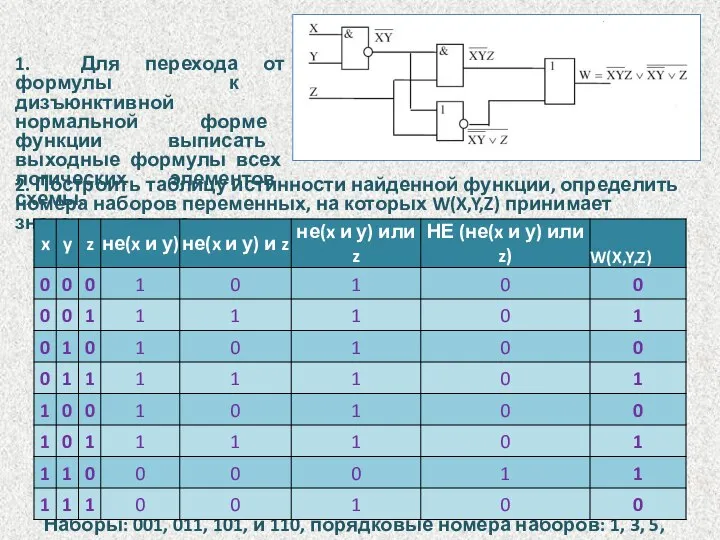
- 21. Переход от логической схемы к формуле функции Пример 2. Задана логическая схема функции W(X,Y,Z). Построить таблицу
- 22. 1. Для перехода от формулы к дизъюнктивной нормальной форме функции выписать выходные формулы всех логических элементов
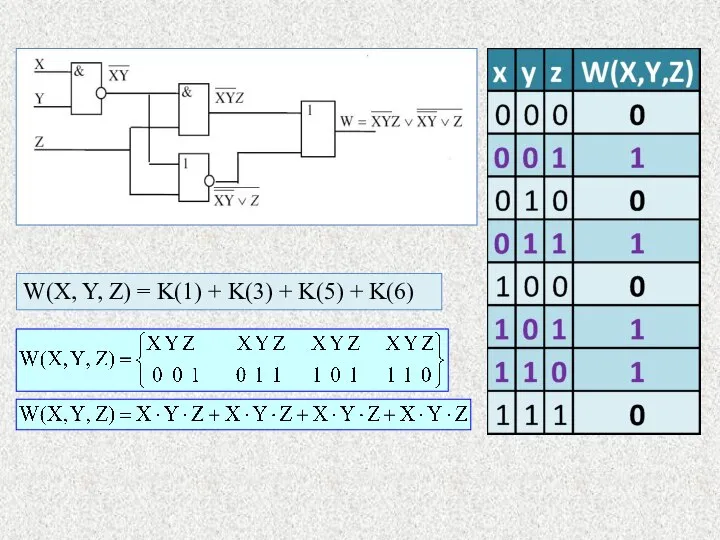
- 23. W(X, Y, Z) = K(1) + K(3) + K(5) + K(6)
- 24. 1. Для перехода от формулы к дизъюнктивной нормальной форме функции выписать выходные формулы всех логических элементов
- 25. Раскрыть все скобки и добавить недостающие переменные умножением членов полученной ДНФ на скобки, равные единице: Раскрыть
- 26. 3. Построить таблицу истинности найденной функции. Сначала определить номера наборов, на которых полученные конституенты равны 1:
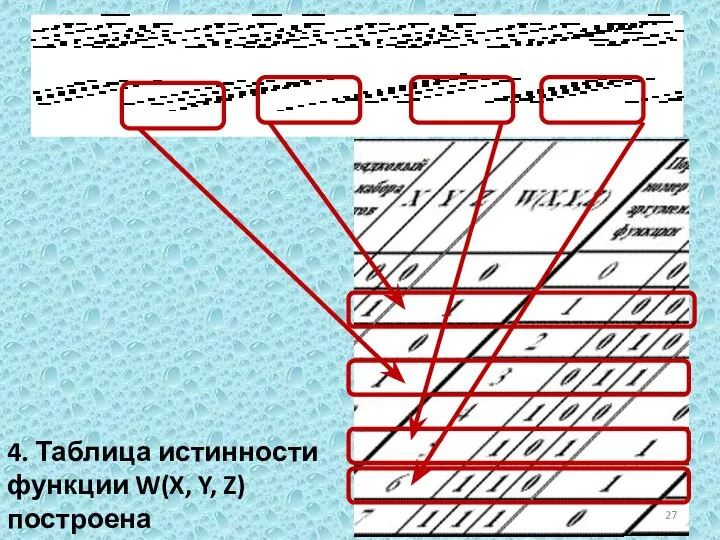
- 27. 4. Таблица истинности функции W(X, Y, Z) построена
- 28. Операцию конъюнкции называют двойственной операции дизъюнкции, а операцию дизъюнкции - двойственной операции конъюнкции. Теорема. Если формулы
- 29. Конъюнктивной нормальной формой (КНФ) функции А(X, Y, Z) называется равносильная ей формула, представляющая собой конъюнкцию элементарных
- 30. Совершенной конъюнктивной нормальной формой (СКНФ ) функции F (x1, x2, … , xn) называется равносильная ей
- 31. СКНФ функции F (x1, x2, … , xn) можно получить: - с помощью таблицы истинности, -
- 32. Построение СКНФ функции по таблице истинности: В таблице истинности отметить наборы аргументов, на которых значение функции
- 33. Правило получения СКНФ функции F с помощью равносильных преобразований Для функции F получить любую КНФ. Затем
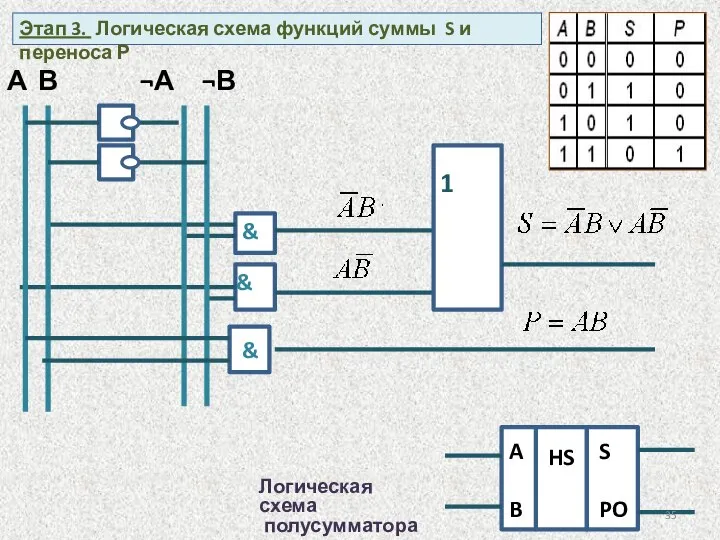
- 34. Этап 1. Построить таблицы истинности функций S и P: S=(A+B) (mod 2), если (А=1 и В=1),
- 35. & & 1 А В ¬А ¬В Логическая схема полусумматора & HS A B S PO
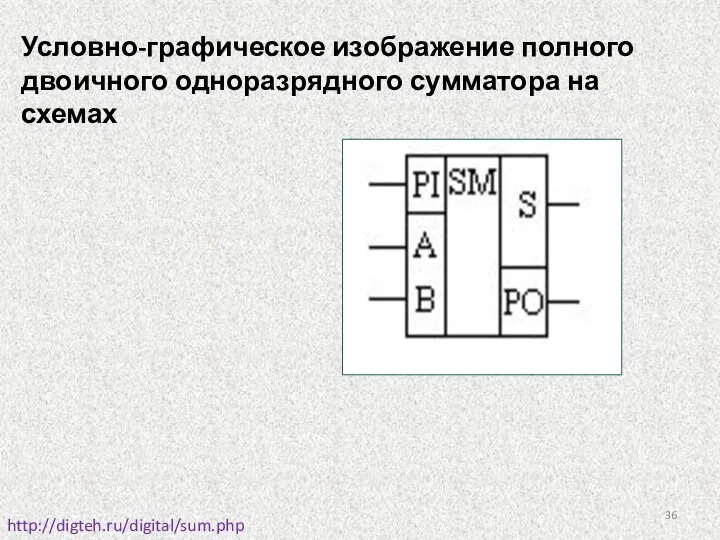
- 36. Условно-графическое изображение полного двоичного одноразрядного сумматора на схемах http://digteh.ru/digital/sum.php
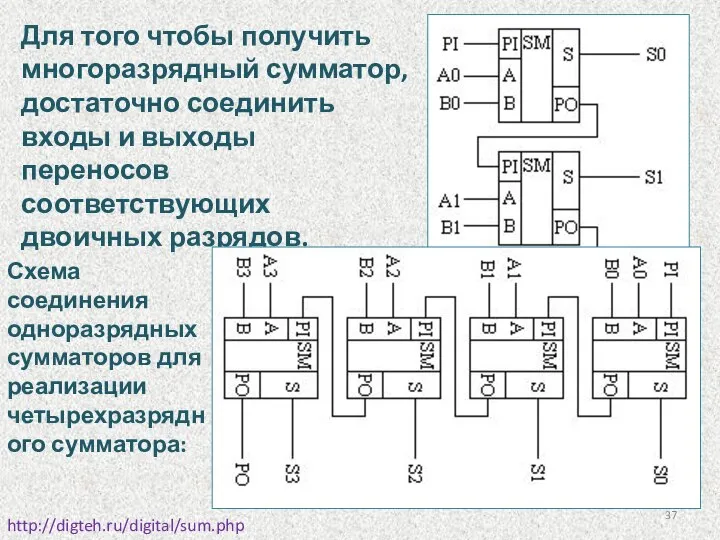
- 37. Для того чтобы получить многоразрядный сумматор, достаточно соединить входы и выходы переносов соответствующих двоичных разрядов. http://digteh.ru/digital/sum.php
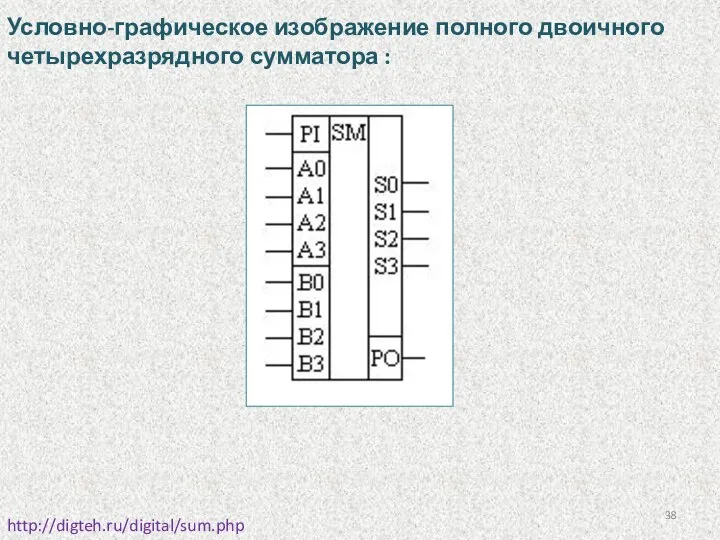
- 38. Условно-графическое изображение полного двоичного четырехразрядного сумматора : http://digteh.ru/digital/sum.php
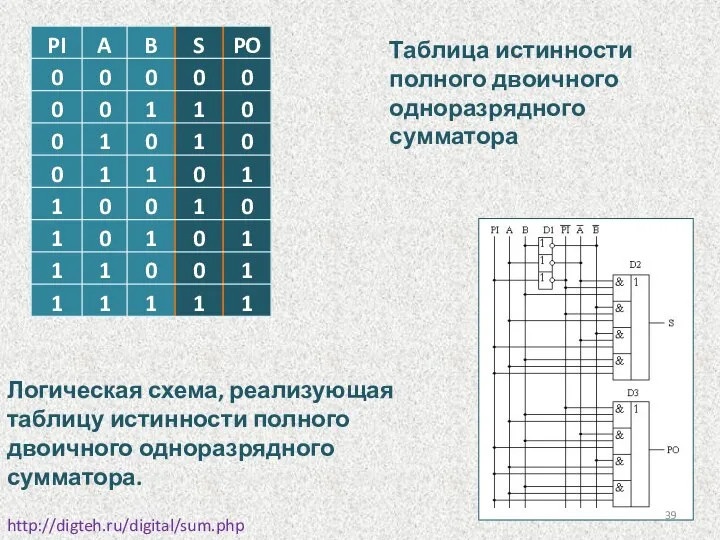
- 39. Таблица истинности полного двоичного одноразрядного сумматора http://digteh.ru/digital/sum.php Логическая схема, реализующая таблицу истинности полного двоичного одноразрядного сумматора.
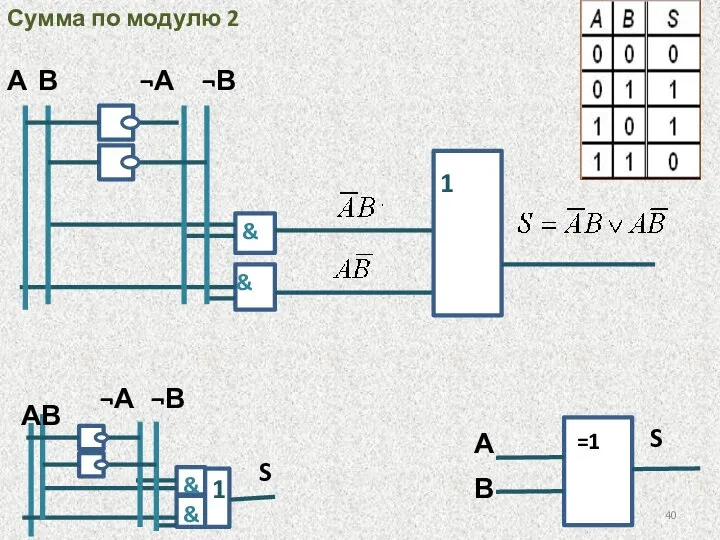
- 40. & & 1 А В ¬А ¬В Сумма по модулю 2 ¬А ¬В =1 А В
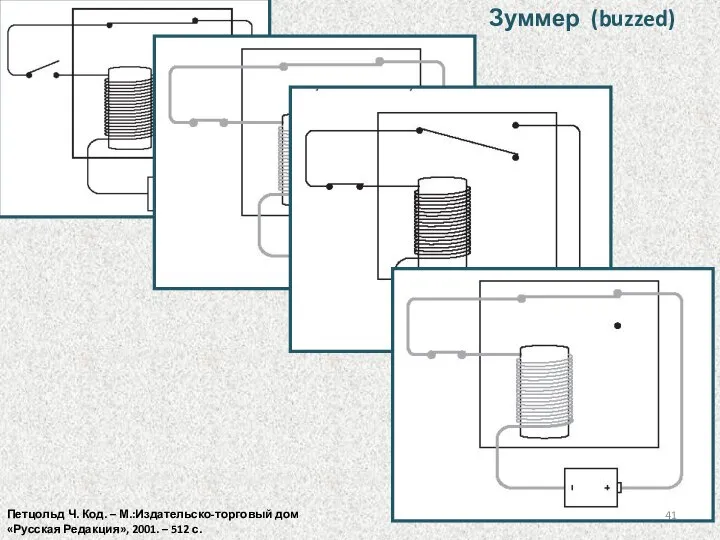
- 41. Зуммер (buzzed) Петцольд Ч. Код. – М.:Издательско-торговый дом «Русская Редакция», 2001. – 512 с.
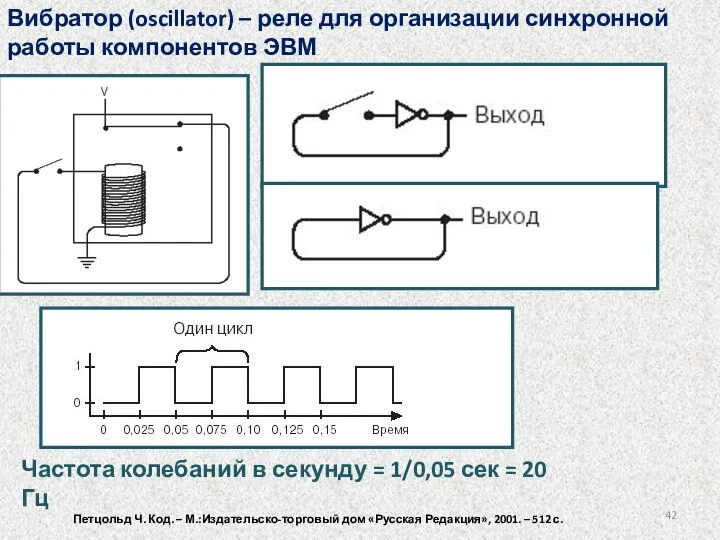
- 42. Вибратор (oscillator) – реле для организации синхронной работы компонентов ЭВМ Частота колебаний в секунду = 1/0,05
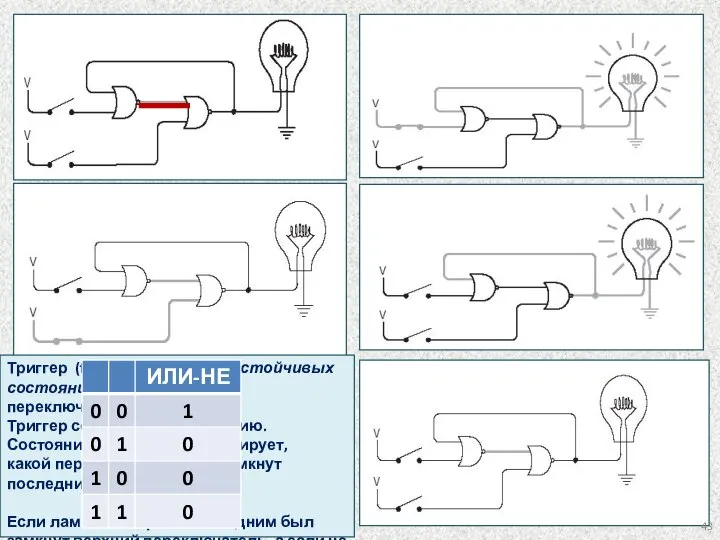
- 43. Триггер (flip-flop) имеет два устойчивых состояния при разомкнутых переключателях. Триггер сохраняет информацию. Состояние триггера сигнализирует, какой
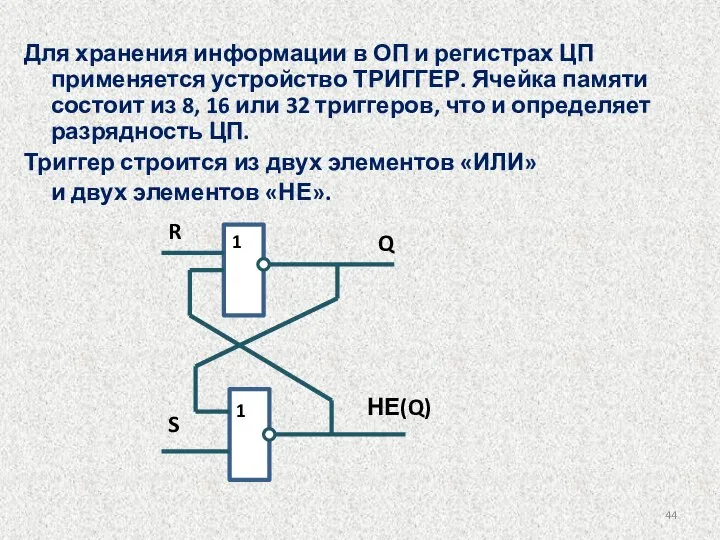
- 44. Для хранения информации в ОП и регистрах ЦП применяется устройство ТРИГГЕР. Ячейка памяти состоит из 8,
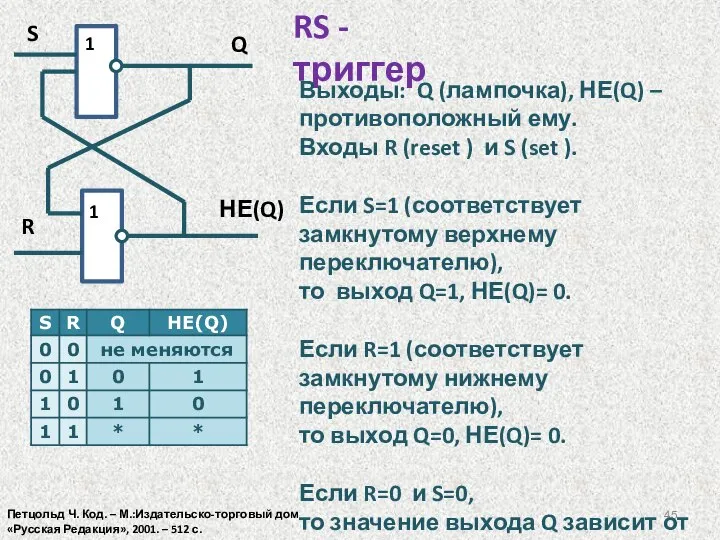
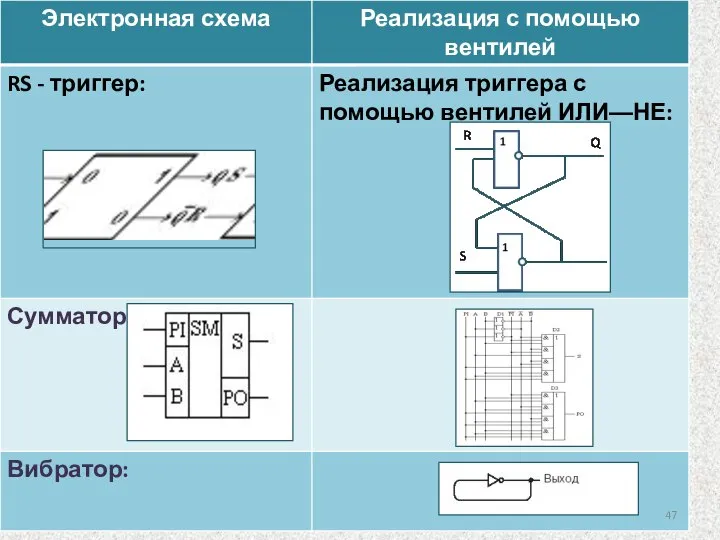
- 45. RS - триггер Выходы: Q (лампочка), НЕ(Q) – противоположный ему. Входы R (reset ) и S
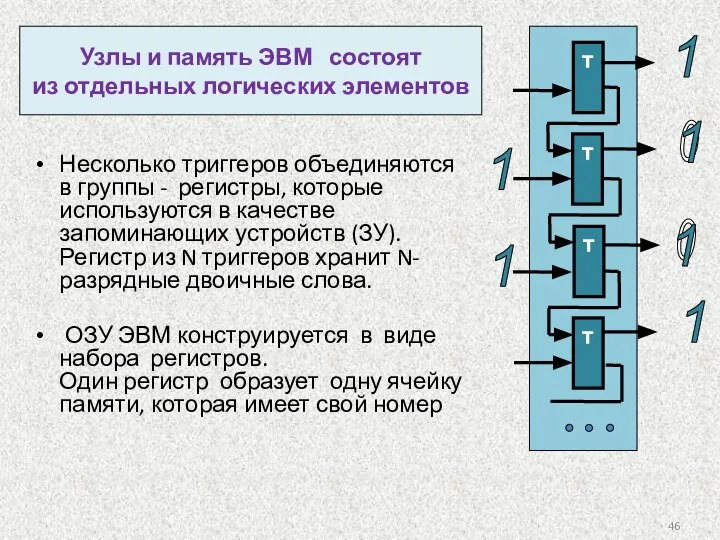
- 46. Несколько триггеров объединяются в группы - регистры, которые используются в качестве запоминающих устройств (ЗУ). Регистр из
- 49. Скачать презентацию


















 Основы деятельности финансового менеджера
Основы деятельности финансового менеджера ФАРМАКОТЕРАПИЯ ПРИ ГИПЕРТОНИЧЕСКОЙ БОЛЕЗНИ
ФАРМАКОТЕРАПИЯ ПРИ ГИПЕРТОНИЧЕСКОЙ БОЛЕЗНИ 02.05 Голова и ее элементы
02.05 Голова и ее элементы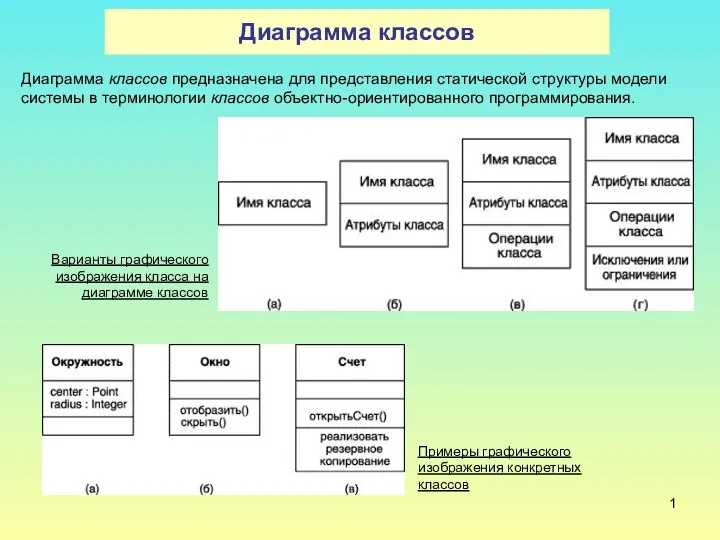 Диаграмма классов
Диаграмма классов Центр народной культуры Карелии
Центр народной культуры Карелии  Правоохранительная деятельность таможенных органов Подготовили: Рыбалко В. и Волчёнков А. Группа 1309
Правоохранительная деятельность таможенных органов Подготовили: Рыбалко В. и Волчёнков А. Группа 1309 Обзор информационных технологий, используемых в учебном процессе, для демонстраций Автор: Махрова Л.В.
Обзор информационных технологий, используемых в учебном процессе, для демонстраций Автор: Махрова Л.В. Особенности проектирования зданий для сейсмических районов
Особенности проектирования зданий для сейсмических районов Линии передачи электромагнитных волн. Проволочные и кабельные линии передачи радиоволн. (Тема 1.2)
Линии передачи электромагнитных волн. Проволочные и кабельные линии передачи радиоволн. (Тема 1.2) Развитие психологии, как науки в XVIII-XIX веках в Западных странах.
Развитие психологии, как науки в XVIII-XIX веках в Западных странах.  Britain: Traditions, Customs and Holidays. The English Year
Britain: Traditions, Customs and Holidays. The English Year Функции по защите информации руководителя предприятия
Функции по защите информации руководителя предприятия Презентация «Табель о рангах» Таможенные чины.
Презентация «Табель о рангах» Таможенные чины. Геймеры. Учим играть в игры
Геймеры. Учим играть в игры Business etiquette
Business etiquette Формы работы на уроках математики в коррекционных классах Учитель математики ГБОУ СОШ № 201 Бадаева Екатерина Викторовна
Формы работы на уроках математики в коррекционных классах Учитель математики ГБОУ СОШ № 201 Бадаева Екатерина Викторовна Презентация ИСТОРИЯ ОТКРЫТКИ
Презентация ИСТОРИЯ ОТКРЫТКИ  Игра. Административная этика как вид профессиональной этики
Игра. Административная этика как вид профессиональной этики Социальные общности, как политические акторы
Социальные общности, как политические акторы Реорганизация органов безопасности ссср
Реорганизация органов безопасности ссср  ОПЕРАЦІЙНА СИСТЕМА MS DOS. ОСНОВНІ ПОНЯТТЯ Призначення операційної системи Поняття файлу. Способи звертання до файлу Організація
ОПЕРАЦІЙНА СИСТЕМА MS DOS. ОСНОВНІ ПОНЯТТЯ Призначення операційної системи Поняття файлу. Способи звертання до файлу Організація  Воспитание
Воспитание Модели рабочих мест (должностей)
Модели рабочих мест (должностей) Тема 1. Финансы предприятий и финансовый менеджмент
Тема 1. Финансы предприятий и финансовый менеджмент  Статистика поломок систем вентиляции и кондиционирования
Статистика поломок систем вентиляции и кондиционирования Презентация на тему "Система работы с одарёнными детьми" - скачать презентации по Педагогике
Презентация на тему "Система работы с одарёнными детьми" - скачать презентации по Педагогике Прикладне програмування. Методи та засоби реєстрації та відтворення сигналів
Прикладне програмування. Методи та засоби реєстрації та відтворення сигналів Физическая культура в общекультурной и профессиональной подготовке студентов
Физическая культура в общекультурной и профессиональной подготовке студентов