Содержание
- 2. Проблема В настоящее время накоплен значительный экспериментальный и теоретический материал по ползучести бетона. Вместе с тем
- 3. Цель исследований Разработка и программная реализация алгоритма метода конечных элементов для решения плоской задачи теории наследственного
- 4. Наследственные функции II рода для бетона Операторно-матричной форма физических соотношений , где векторы напряжений и деформаций
- 5. Величину принимаем равной 2 сут. , (1) Теория старения Ядро релаксации где функция меры ползучести Н.Х.
- 6. , где введены обозначения: (2)
- 7. Теория наследственного старения Функция меры ползучести С.В. Александровского . (3) Здесь обозначено: ; - опытные константы.
- 8. После обработки выражения (4) символьным процессором системы Maple 12 и группировки членов получим следующую формулу для
- 9. где
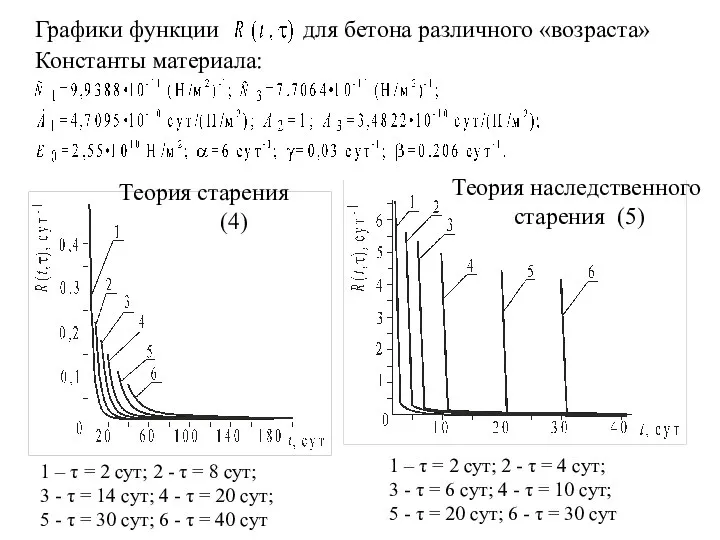
- 10. Графики функции для бетона различного «возраста» Теория старения (4) Теория наследственного старения (5) 1 – τ
- 11. Конечноэлементная реализация плоской задачи теории ползучести Векторы-столбцы наследственных деформаций и перемещений Отсюда где - матрица, образованная
- 12. Здесь обозначено: - матрица, устанавливающая связь ; - объем, занимаемый КЭ; поверхность КЭ, к которой приложена
- 13. Для вычисления интеграла воспользуемся численным методом, основанном на формуле трапеций. Разобьем рассматриваемый временной интервал на m
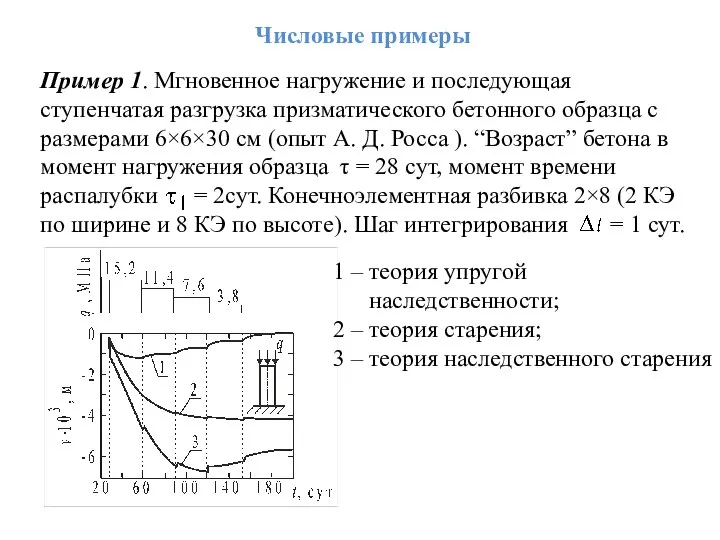
- 14. Пример 1. Мгновенное нагружение и последующая ступенчатая разгрузка призматического бетонного образца с размерами 6×6×30 см (опыт
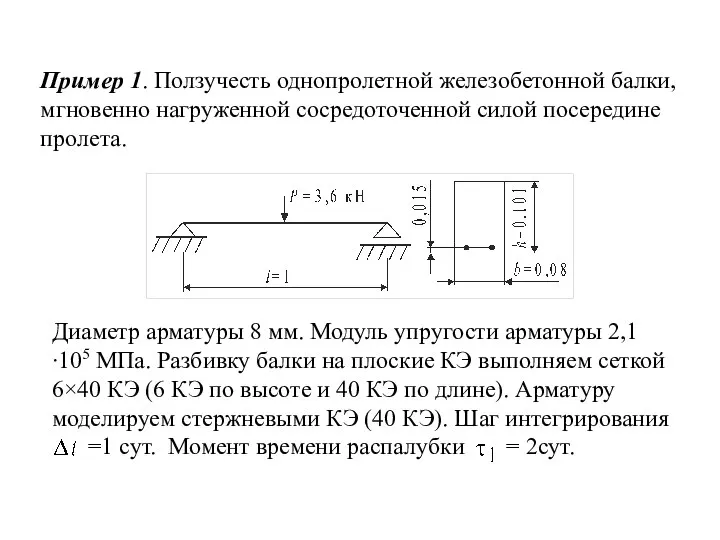
- 15. Пример 1. Ползучесть однопролетной железобетонной балки, мгновенно нагруженной сосредоточенной силой посередине пролета. Диаметр арматуры 8 мм.
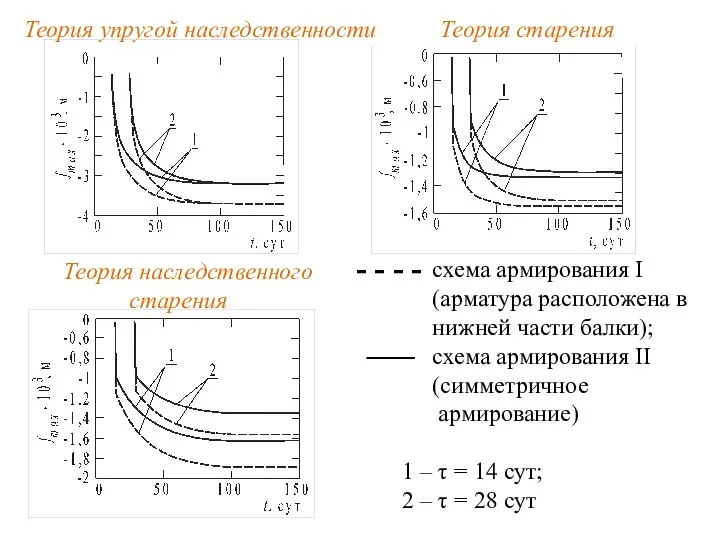
- 16. схема армирования I (арматура расположена в нижней части балки); схема армирования II (симметричное армирование) 1 –
- 17. Выводы: В рамках теории старения и теории наследственного старения с помощью символьного процессора системы Maple 12
- 19. Скачать презентацию




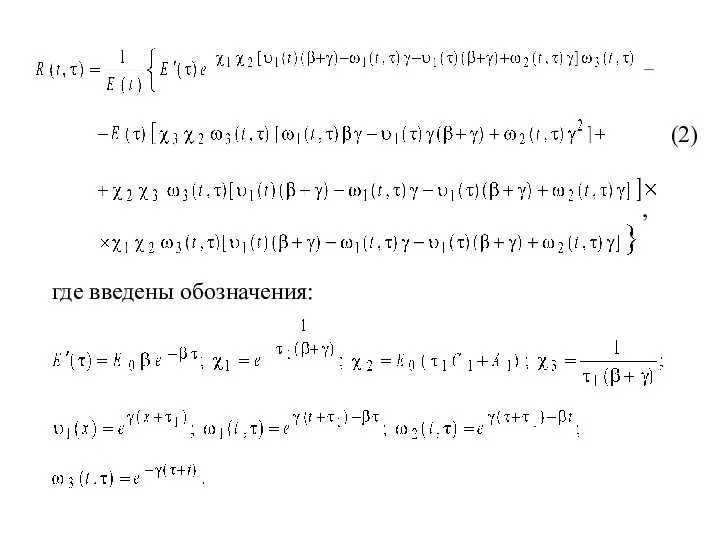


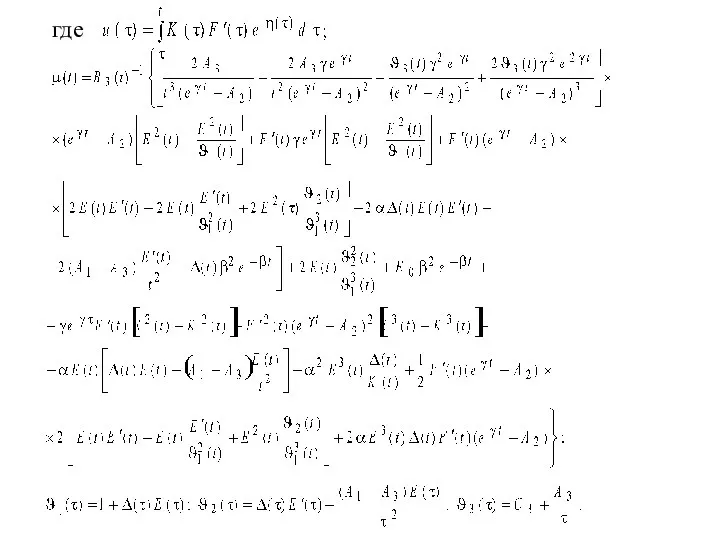




 Мультимедийные устройства
Мультимедийные устройства Persönliche Endungen von Verben
Persönliche Endungen von Verben Informatyka i ekonometria
Informatyka i ekonometria Энзиология - 2 (ЛФ).ppt
Энзиология - 2 (ЛФ).ppt Италия. Рим и Ватикан
Италия. Рим и Ватикан Основные вопросы клинической фармакологии
Основные вопросы клинической фармакологии Презентация Маркетинговая среда
Презентация Маркетинговая среда Решение тригонометрических уравнений
Решение тригонометрических уравнений  Автор Работы: Студентка Группы 60301c Мельникова К.В. Руководитель: Старший Преподаватель Ловкис Л.К. Презентация дипломной ра
Автор Работы: Студентка Группы 60301c Мельникова К.В. Руководитель: Старший Преподаватель Ловкис Л.К. Презентация дипломной ра Флокирование дронов с помощью децентрализованной модели интеллектуального управления
Флокирование дронов с помощью децентрализованной модели интеллектуального управления Механизмы нитепритягивателя челночных швейных машин
Механизмы нитепритягивателя челночных швейных машин Creative heritage of F.W. Taylor and main provisions of Taylorism
Creative heritage of F.W. Taylor and main provisions of Taylorism Дипломный проект на тему: «Разработка программно-математических средств для обнаружения сигнала системы спутникового позиционир
Дипломный проект на тему: «Разработка программно-математических средств для обнаружения сигнала системы спутникового позиционир Политическое поведение
Политическое поведение Устройства сопряжения
Устройства сопряжения мой путь к доброте - презентация для начальной школы
мой путь к доброте - презентация для начальной школы Совет Безопасности ООН. (Тема 6)
Совет Безопасности ООН. (Тема 6) ЭМИССИЯ ЭЛЕКТРОНОВ ИЗ ПРОВОДНИКОВ. КОНТАКТНЫЕ ЯВЛЕНИЯ НА ГРАНИЦАХ ПРОВОДНИКОВ
ЭМИССИЯ ЭЛЕКТРОНОВ ИЗ ПРОВОДНИКОВ. КОНТАКТНЫЕ ЯВЛЕНИЯ НА ГРАНИЦАХ ПРОВОДНИКОВ Узоры и орнаменты - презентация для начальной школы_
Узоры и орнаменты - презентация для начальной школы_ Россия – многонациональная культура
Россия – многонациональная культура Элементарный состав
Элементарный состав Показатели времени в китайском языке. Правила употребления
Показатели времени в китайском языке. Правила употребления Правила игры в баскетбол
Правила игры в баскетбол микоплазмоз в.к.
микоплазмоз в.к. ФСБ РФ Понятие,структура,полномочия
ФСБ РФ Понятие,структура,полномочия  Junior Achievement Магдалена Малеева, gorichka.bg. - презентация
Junior Achievement Магдалена Малеева, gorichka.bg. - презентация Характеристики современных ПК. Устройства и принцип действие ЭВМ
Характеристики современных ПК. Устройства и принцип действие ЭВМ Анализ основных достижений ученых досоветского периода
Анализ основных достижений ученых досоветского периода