Содержание
- 2. Лекция 3 Слайд 2 Кулоновский потенциал взаимодействия U(r) = α/r (где α = q1q2) – один
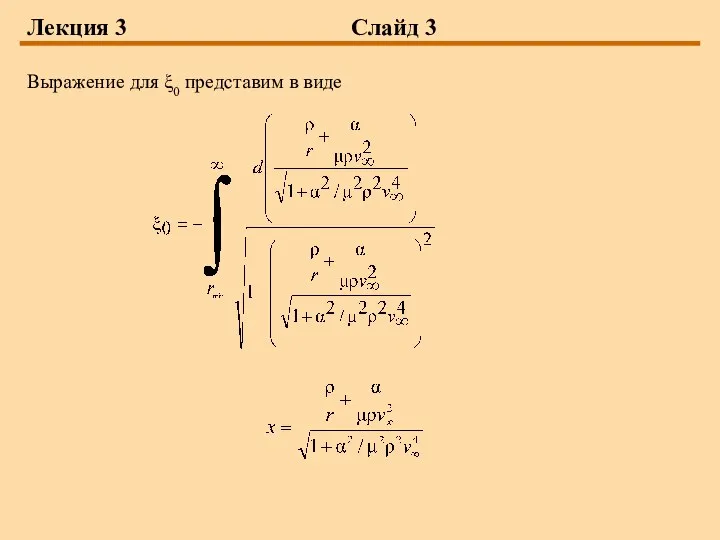
- 3. Лекция 3 Слайд 3 Выражение для ξ0 представим в виде
- 4. Лекция 3 Слайд 4 получим табличный интеграл где Представив получим Так как ξ0 = (π –
- 5. Лекция 3 Слайд 5 В соответствии с общим определением дифференциального сечения Так как 2μv∞2 = 4(m1v∞2/2)m2/(m1+m2)
- 6. Лекция 3 Слайд 6 Для того чтобы выразить sin4(χ) через угол θ воспользуемся тригонометрическим равенством где
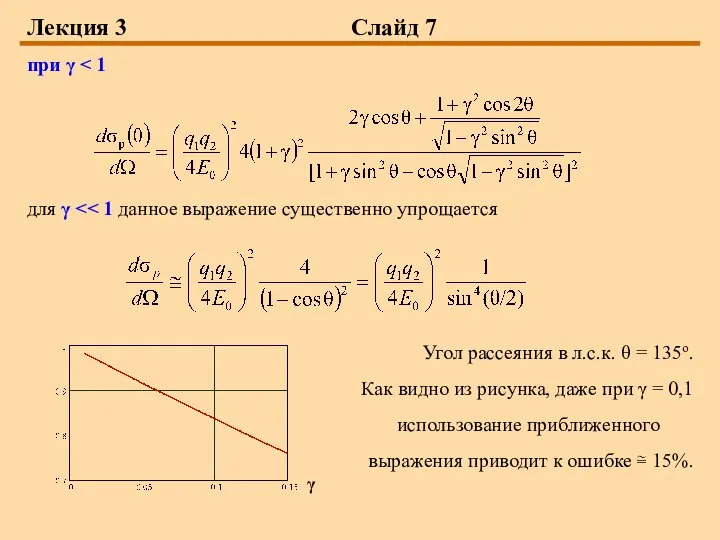
- 7. Лекция 3 Слайд 7 при γ для γ Угол рассеяния в л.с.к. θ = 135о. Как
- 8. Лекция 3 Слайд 8 Дифференциальное сечения рассеяния как функция переданной энергии E2 частице m2 , т.е.
- 9. Лекция 3 Слайд 9 окончательно, имеем При упругом рассеянии в кулоновском потенциале наиболее вероятны малые углы
- 10. Лекция 3 Слайд 10
- 11. Лекция 3 Слайд 11 Для описания рассеяния пучка используется понятие дифференциального сечения рассеяния dσ, определяемого следующим
- 12. Лекция 3 Слайд 12 В случае однородного пучка и сферически симметричного потенциала взаимодействия число таких частиц
- 14. Скачать презентацию









 Наши национальные денежные знаки - презентация для начальной школы_
Наши национальные денежные знаки - презентация для начальной школы_ Обробка інформації в обліковій системі
Обробка інформації в обліковій системі Кормушки для птиц
Кормушки для птиц кредитно-денежная система
кредитно-денежная система P-Урок 04 Равномерное прямолинейное движение
P-Урок 04 Равномерное прямолинейное движение Кафедра микробиологии, вирусологии и иммунологии КазНМУ Электронное пособие на тему: Алгоритм лабораторной диагностики уроге
Кафедра микробиологии, вирусологии и иммунологии КазНМУ Электронное пособие на тему: Алгоритм лабораторной диагностики уроге Лесли Алвин Уайт
Лесли Алвин Уайт Чарльз Роберт Дарвин: фрагменты жизни
Чарльз Роберт Дарвин: фрагменты жизни Разработка Internet- и Web-приложений. Изучаем JavaScript. (Лекция 4)
Разработка Internet- и Web-приложений. Изучаем JavaScript. (Лекция 4) Event-менеджмент Выполнили Симбирская О. В. , Шаляпина О. Н., МАОУ «Гимназия №2» В. Новгород 2012 год
Event-менеджмент Выполнили Симбирская О. В. , Шаляпина О. Н., МАОУ «Гимназия №2» В. Новгород 2012 год Презентация "УПРАВЛЕНИЕ КАЧЕСТВОМ логистических процессов" - скачать презентации по Экономике
Презентация "УПРАВЛЕНИЕ КАЧЕСТВОМ логистических процессов" - скачать презентации по Экономике Обработка ошибок
Обработка ошибок Organization of the Diplomatic protocol in Italy
Organization of the Diplomatic protocol in Italy Производственная практика. ООО «Сибирская ярмарка»
Производственная практика. ООО «Сибирская ярмарка» Филимоновская игрушка
Филимоновская игрушка Техника торцевания
Техника торцевания Содержание курса - Как стать успешным в XXI веке?Содержание курса Эти навыки дает программа «Учимся с INTEL» - 15 занятий! Расписание зан
Содержание курса - Как стать успешным в XXI веке?Содержание курса Эти навыки дает программа «Учимся с INTEL» - 15 занятий! Расписание зан Художник- портретист Александр Шилов Учитель русского языка и литературы Жукова Татьяна Анатольевна
Художник- портретист Александр Шилов Учитель русского языка и литературы Жукова Татьяна Анатольевна Нейрофизиология программы
Нейрофизиология программы  Винайдення автобуса
Винайдення автобуса ГЕОЛОГИЧЕСКАЯ ДЕЯТЕЛЬНОСТЬ РЕК И ВРЕМЕННЫХ ПОТОКОВ
ГЕОЛОГИЧЕСКАЯ ДЕЯТЕЛЬНОСТЬ РЕК И ВРЕМЕННЫХ ПОТОКОВ Нейронная регуляция 1. Отличие нейронной регуляции от гуморальной. 2. Рефлекторный принцип регуляции. 3. Физиологическая харак
Нейронная регуляция 1. Отличие нейронной регуляции от гуморальной. 2. Рефлекторный принцип регуляции. 3. Физиологическая харак Интеграция различных подходов к менеджменту Выполнил: Студент 41 БЖД Гильматдинов М.М.
Интеграция различных подходов к менеджменту Выполнил: Студент 41 БЖД Гильматдинов М.М. Договор синдицированного кредита по российскому праву Иван Борисов Vice President, Legal counsel
Договор синдицированного кредита по российскому праву Иван Борисов Vice President, Legal counsel  Художник-воин-патриот Монографический урок по творчеству Василия Васильевича Верещагина 1842-1904
Художник-воин-патриот Монографический урок по творчеству Василия Васильевича Верещагина 1842-1904 Музеи. Парки. Усадьбы
Музеи. Парки. Усадьбы Праздник Святой Троицы
Праздник Святой Троицы История возникновения петербургской росписи
История возникновения петербургской росписи