Содержание
- 2. Системы счисления Позиционные системы счисления Каждая позиционная система счисления определяется некоторым числом b > 1 (т.
- 3. Системы счисления И+ПРГ
- 4. Системы счисления Непозиционные системы счисления Римская система счисления Римская система нумерации с помощью букв была распространена
- 5. Поразрядно с переходом в старший разряд при сложении или заимствовании из старшего разряда при вычитании). Системы
- 6. Системы счисления Перевод чисел из десятичной позиционной системы счисления в другую и наоборот При переводе целого
- 8. Скачать презентацию
Системы счисления
Позиционные системы счисления
Каждая позиционная система счисления определяется некоторым числом
Системы счисления
Позиционные системы счисления
Каждая позиционная система счисления определяется некоторым числом
Число x в b-ричной системе счисления представляется в виде линейной комбинации степеней числа b:
где ak — это целые числа, называемые цифрами, удовлетворяющие неравенству 0 ≤ ak < b,
k - порядковый номер разряда начиная с нулевого, n – количество разрядов.
Каждая степень bk в такой записи называется разрядом, старшинство разрядов и соответствующих им цифр определяется значением показателя k.
Число x записывают в виде последовательности его b-ричных цифр, перечисляемых по убыванию старшинства разрядов слева направо:
X = an-1an-2 … a0
Например, число сто три представляется в десятичной системе счисления в виде: 103 = 1*102+0*101+3*100, а дробь 0,25 = 2*10-1+5*10-2
И+ПРГ
Системы счисления
И+ПРГ
Системы счисления
И+ПРГ
Системы счисления
Непозиционные системы счисления
Римская система счисления
Римская система нумерации с помощью
Системы счисления
Непозиционные системы счисления
Римская система счисления
Римская система нумерации с помощью
Для закрепления в памяти буквенных обозначений римских цифр в порядке убывания существует мнемоническое правило:
Мы Дарим Сочные Лимоны, Хватит Всем И ещё останется.
Соответственно M, D, C, L, X, V, I
Натуральные числа записываются при помощи повторения этих цифр. При этом, если большая цифра стоит перед меньшей, то они складываются (принцип сложения), если же меньшая - перед большей, то меньшая вычитается из большей (принцип вычитания). Последнее правило применяется только во избежание четырёхкратного повторения одной и той же цифры. Например, I, Х, С ставятся соответственно перед Х, С, М для обозначения 9, 90, 900 или перед V, L, D для обозначения 4, 40, 400.
Например, VI = 5+1 = 6, IV = 5 - 1 = 4 (вместо IIII). XIX = 10 + 10 - 1 = 19 (вместо XVIIII), XL = 50 - 10 =40 (вместо XXXX), XXXIII = 10 + 10 + 10 + 1 + 1 + 1 = 33 и т.д.
Система остаточных классов (СОК) - представление числа в системе остаточных классов основано на понятии вычета и китайской теореме об остатках.
Система счисления Штерна-Броко – способ записи положительных рациональных чисел, основанный на дереве Штерна-Броко.
И+ПРГ
Поразрядно с переходом в старший разряд при сложении или заимствовании
Поразрядно с переходом в старший разряд при сложении или заимствовании
Системы счисления
Операции в системах счисления
Позиционная
Непозиционная
Сложение и вычитание
Умножение
Сложение -> Посимвольно, путем "склеивания" символов-цифр и последующей замены (слева направо) 4-х подряд расположенных символов на группы из 2-х символов имеющих то же значение (например, IIII на IV).
Вычитание -> посимвольно, обратной операцией "разбиения" символов на составляющие меньшего номинала.
Умножение каждой цифры множимого на каждую цифру множителя и сложение полученных произведений с поразрядным сдвигом результата в соответствии с разрядами множителя.
Умножение каждой цифры множимого на каждую цифру множителя и сложение полученных произведений, при этом цифры одинакового порядка для удобства ставим одну под другой.
Из старших разрядов делимого группируется число - субделимое, которое можно разделить на делитель (равное делителю по количеству цифр или на одну цифру больше). К остатку от деления добавляются цифры делимого (ещё не участвовавшие в процессе деления) для формирования нового субделимого, и так пока не будет использован младший разряд делимого.
Умножая делитель на ряд чисел (например, на сто – C, 50 – L, десять – X, двадцать – XX) и сравнивая произведение с делимым – находим старшие числа частного. Отнимаем их от делимого и снова повторяем операцию до получения конечного результата: нахождения остатка от деления.
Деление
Перевод числа из одной системы счисления в другую
Переводе между позиционной и смешенной системами осуществляется поразрядным преобразованием числа. Перевод между непозиционной и другими системами осуществляется путем преобразования в (из) цифр непозиционной системы в позиционную (смешанную).
И+ПРГ
Системы счисления
Перевод чисел из десятичной позиционной системы счисления
в другую и
Системы счисления
Перевод чисел из десятичной позиционной системы счисления
в другую и
При переводе целого числа (целой части числа) из десятичной системы счисления в любую другую: исходное число (или целую часть) надо разделить на основание системы счисления, в которую выполняется перевод. Деление выполнять, пока частное не станет меньше основания новой системы счисления. Результат перевода определяется остатками от деления: первый остаток дает младшую цифру результирующего числа, последнее частное от деления дает старшую цифру.
При переводе правильной дроби из десятичной системы счисления в любую другую систему счисления дробь следует умножать на основание системы счисления, в которую выполняется перевод. Полученная после первого умножения целая часть является старшим разрядом результирующего числа. Умножение вести до тех пор пока произведение станет равным нулю или не будет получено требуемое число знаков после разделительной точки.
При переводе вещественных чисел целая и дробная части числа переводятся отдельно.
Перевод числа из двоичной системы в системы с основанием, равным степеням двойки (8 и 16). Для того чтобы целое двоичное число записать в системе счисления с основанием 2n, нужно данное двоичное число разбить справа налево на группы по n-цифр в каждой; если в последней левой группе окажется меньше n разрядов, то дополнить ее нулями до нужного числа разрядов; рассмотреть каждую группу, как n-разрядное двоичное число, и заменить ее соответствующей цифрой в системе счисления с основанием 2n.
Перевод числа с основанием, равным степеням двойки (8 и 16) в двоичную осуществляется заменой каждой цифры числа с основанием 2n на эквивалентную ей группу из n двоичных цифр (3 – для восьмеричной системы и 4 для шестнадцатеричной).
Операция перевода в десятичную систему выглядит гораздо проще, так как любое десятичное число можно представить в виде x = a0·pn + a1·pn–1 +... + an–1·p1 + an·p0, где
a0 ... an – это цифры данного числа в системе счисления с основанием p.
Например, перевести число 4A3F в десятичную систему.
По определению, 4A3F= 4·163 + A·162 + 3·161 + F ·160.
При замене A на 10, а F на 15, получается 4·163 + 10·162 + 3·16 + 15·1 = 19007.
И+ПРГ





 Малинина Алена Викторовна Учитель черчения и изобразительного искусства МОУ « СОШ № 12» город Усолье-Сибирс
Малинина Алена Викторовна Учитель черчения и изобразительного искусства МОУ « СОШ № 12» город Усолье-Сибирс Прием документации и зачисление в организации образования
Прием документации и зачисление в организации образования Ваш праздник
Ваш праздник Компьютерные сети
Компьютерные сети Культура Древней Индии
Культура Древней Индии Учитель английского языка Евсюкова И.А. МОУ «Федчёвская ООШ» 2009 год
Учитель английского языка Евсюкова И.А. МОУ «Федчёвская ООШ» 2009 год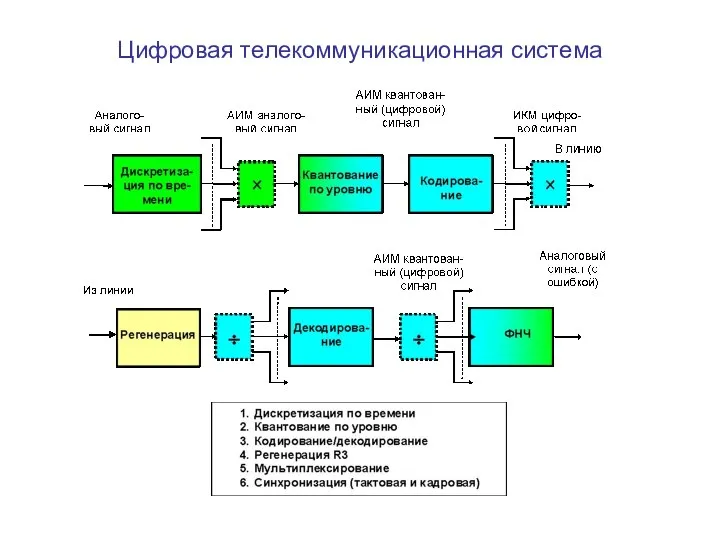 Цифровая телекоммуникационная система
Цифровая телекоммуникационная система Понятие гражданского права, как отрасли права. Источники гражданского права
Понятие гражданского права, как отрасли права. Источники гражданского права Передача информации. Локальные компьютерные сети
Передача информации. Локальные компьютерные сети Плазмозаменители
Плазмозаменители Амнистия. Помилование.Судимость.
Амнистия. Помилование.Судимость. Классы
Классы  Вода и водные устройства
Вода и водные устройства Проект по продвижению комплекса ГТО
Проект по продвижению комплекса ГТО Презентация на тему "Образовательные программы" - скачать презентации по Педагогике
Презентация на тему "Образовательные программы" - скачать презентации по Педагогике Сервисы в Android
Сервисы в Android Элементарные функции
Элементарные функции Компьютерные вирусы
Компьютерные вирусы «МЫ ВЫБИРАЕМ ЗДОРОВЬЕ!!!» «Скажи наркотикам НЕТ !!!» Один мыслитель гулял со своими учениками в саду и отвечал на их вопросы. Потом к
«МЫ ВЫБИРАЕМ ЗДОРОВЬЕ!!!» «Скажи наркотикам НЕТ !!!» Один мыслитель гулял со своими учениками в саду и отвечал на их вопросы. Потом к  XXIII Зимние Олимпийские игры
XXIII Зимние Олимпийские игры Модель методической работы школы на 2011-2012 гг. Цели: активизировать методическую работу школы способствовать повышению професс
Модель методической работы школы на 2011-2012 гг. Цели: активизировать методическую работу школы способствовать повышению професс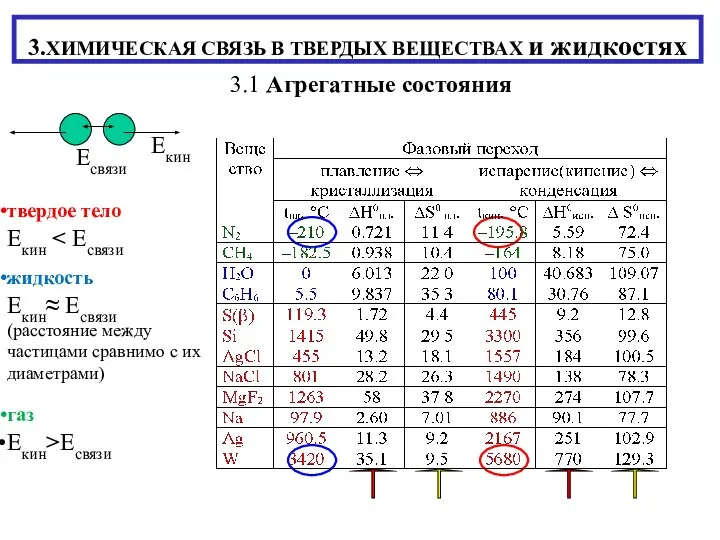 ХИМИЧЕСКАЯ СВЯЗЬ В ТВЕРДЫХ ВЕЩЕСТВАХ и жидкостях
ХИМИЧЕСКАЯ СВЯЗЬ В ТВЕРДЫХ ВЕЩЕСТВАХ и жидкостях Содержание и ремонт цементобетонных покрытий
Содержание и ремонт цементобетонных покрытий Презентация_____
Презентация_____ Разгледайте изразите. В какъв ред ще се извършват действията? Пресметнете ги. 516 – 7. 9 = 115 + 65 : 5 = 1 205. 78 – 96 : 2 = 2 015. 2 – 3 348 : 31 = - презента
Разгледайте изразите. В какъв ред ще се извършват действията? Пресметнете ги. 516 – 7. 9 = 115 + 65 : 5 = 1 205. 78 – 96 : 2 = 2 015. 2 – 3 348 : 31 = - презента Конституционное право РФ
Конституционное право РФ Укажите, в каком случае слово употреблено в прямом значении, а в каком – в переносном. Подберите и запишите синонимы к данным слова
Укажите, в каком случае слово употреблено в прямом значении, а в каком – в переносном. Подберите и запишите синонимы к данным слова Презентация на тему "Управление качество образования в МОУ Лебяженской СОШ Краснотуранского района" - скачать презентации по
Презентация на тему "Управление качество образования в МОУ Лебяженской СОШ Краснотуранского района" - скачать презентации по