Содержание
- 2. Учебные вопросы: 1. Несинусоидальные колебания в электрических цепях. Методы анализа. 2. Спектры типовых сигналов Литература: 1.
- 3. 1. Несинусоидальные воздействия в электрических цепях. Методы анализа В основе методов анализа и синтеза электрических цепей,
- 4. Представляет собой среднее за период значение f(t) (функция f(t) может иметь смысл как тока, так и
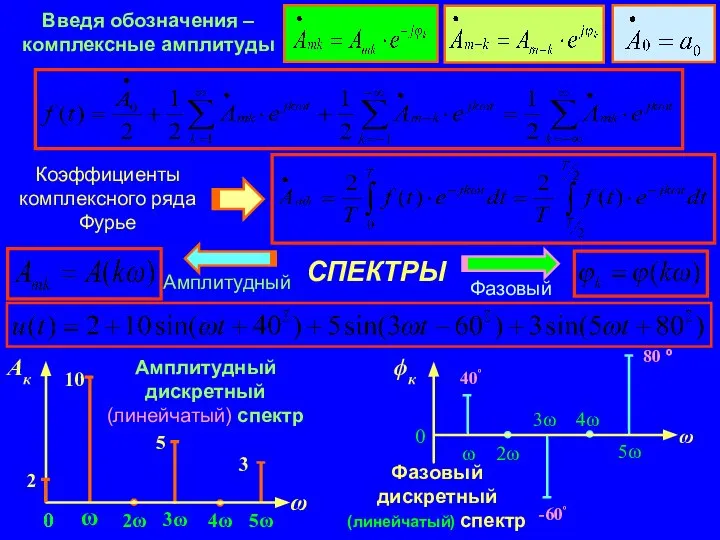
- 5. СПЕКТРЫ Фазовый дискретный (линейчатый) спектр Амплитудный дискретный (линейчатый) спектр
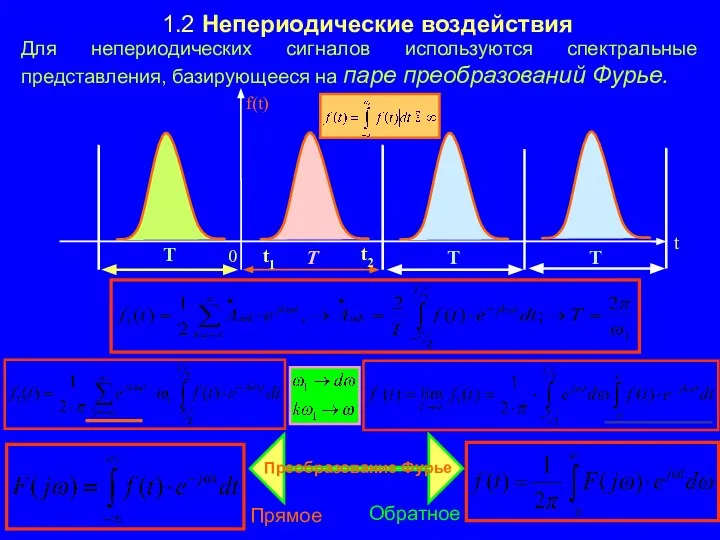
- 6. 1.2 Непериодические воздействия Для непериодических сигналов используются спектральные представления, базирующееся на паре преобразований Фурье.
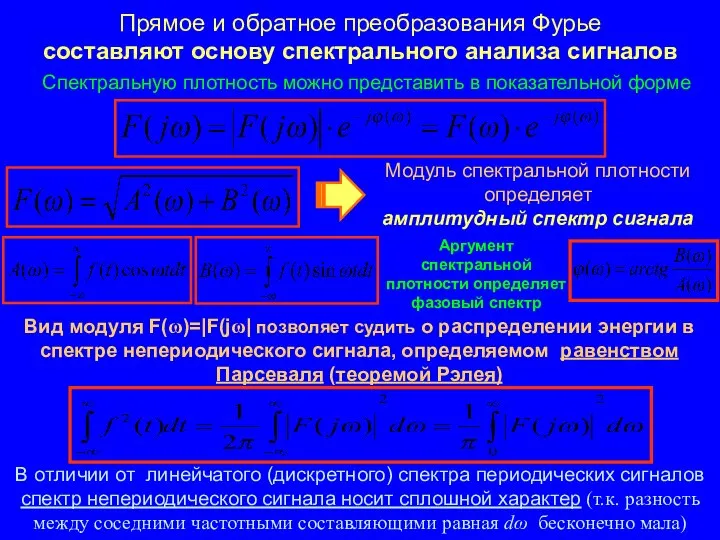
- 7. Прямое и обратное преобразования Фурье составляют основу спектрального анализа сигналов Спектральную плотность можно представить в показательной
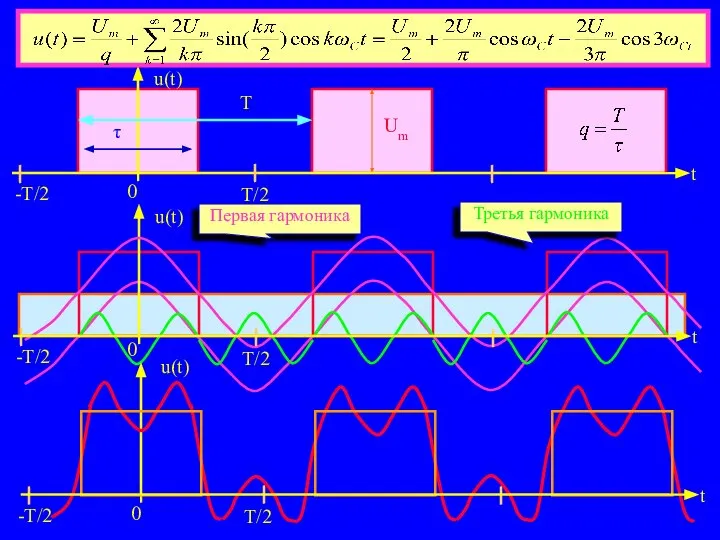
- 8. T/2 -T/2 u(t) Первая гармоника Третья гармоника
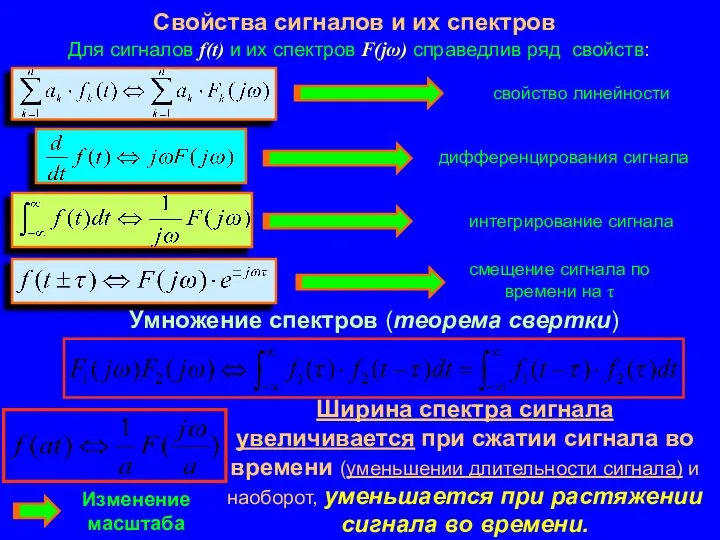
- 9. Свойства сигналов и их спектров Для сигналов f(t) и их спектров F(jω) справедлив ряд свойств: Ширина
- 10. 2. Спектры типовых сигналов Для теоретических и экспериментальных исследований характеристик электрических цепей и передачи сообщений по
- 11. Амплитудный спектр Фазовый спектр Единичная импульсная функция Эта функция является нереализуемой математической абстракцией, однако обладает рядом
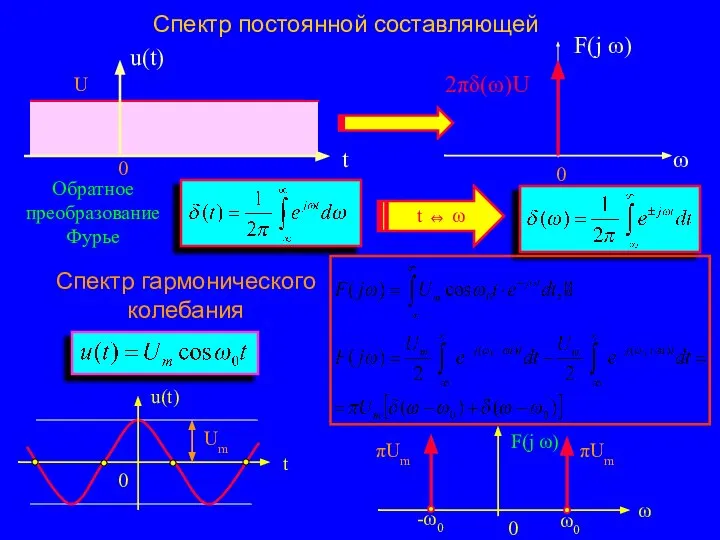
- 12. Спектр постоянной составляющей Спектр гармонического колебания Обратное преобразование Фурье
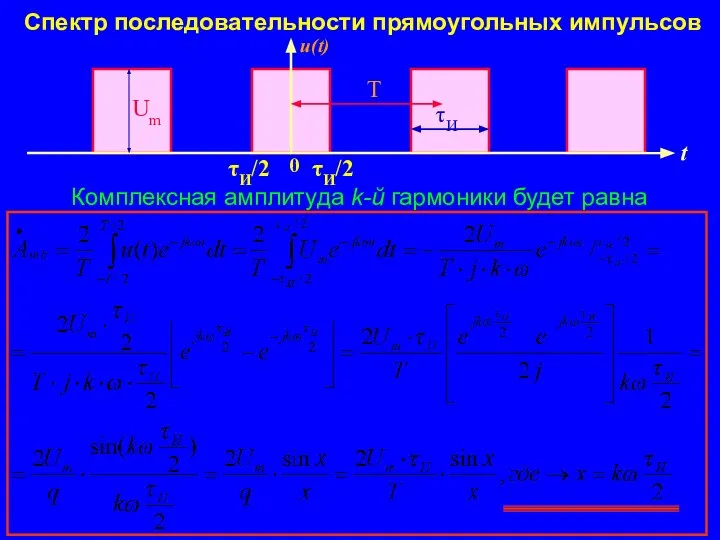
- 13. Спектр последовательности прямоугольных импульсов τИ Комплексная амплитуда k-й гармоники будет равна
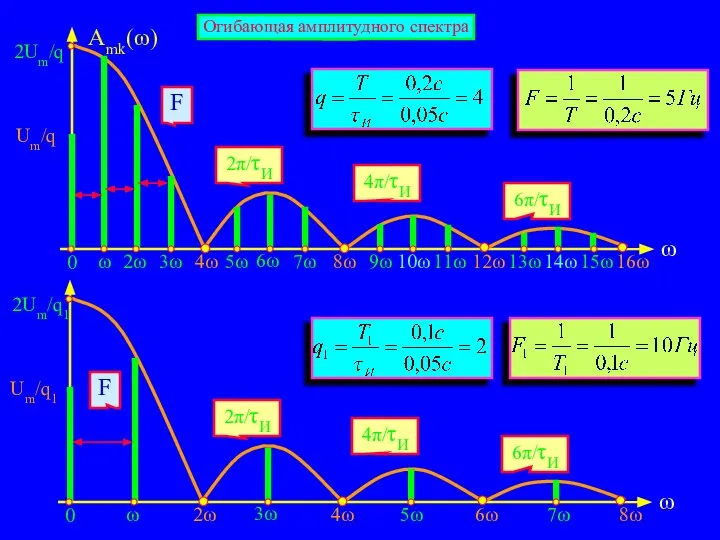
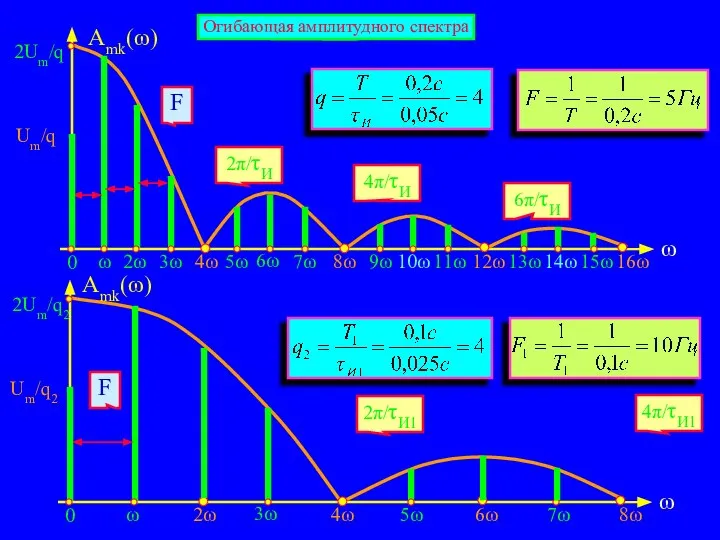
- 15. ω Amk(ω) 2π/τИ 4π/τИ 6π/τИ Огибающая амплитудного спектра
- 16. Амплитудно-частотный спектр такой последовательности импульсов Огибающая амплитудного спектра имеет много лепестков: первый из которых занимает интервал
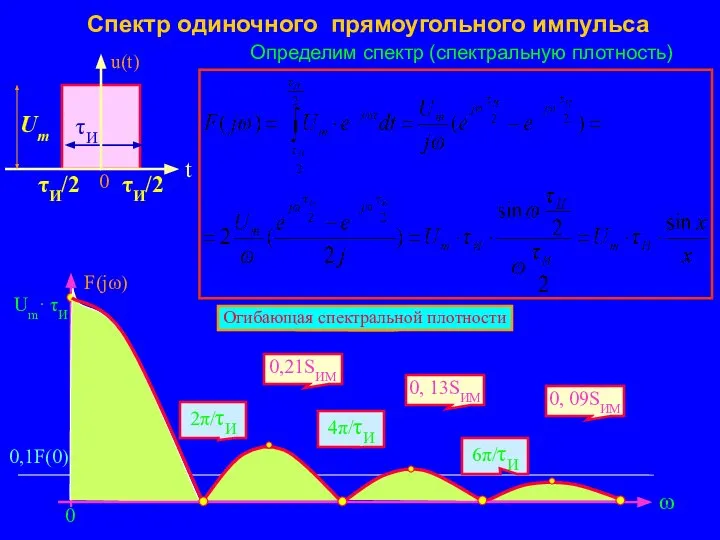
- 18. Спектр одиночного прямоугольного импульса Определим спектр (спектральную плотность)
- 19. Вид графика спектральной плотности Функция спектральной плотности обращается в нуль при значениях аргумента ω·τИ /2 =
- 21. Скачать презентацию








 Широкая масленица
Широкая масленица ЛИТЕР КАЗИНОЛитературный бал При свечах
ЛИТЕР КАЗИНОЛитературный бал При свечах Противоправное поведение как условие гражданско-правовой ответственности
Противоправное поведение как условие гражданско-правовой ответственности Завод FLINS
Завод FLINS  История робототехники
История робототехники Виды статистического наблюдения по фактору времени
Виды статистического наблюдения по фактору времени Deutsch in der modernen Musik
Deutsch in der modernen Musik Изобразительное искусство
Изобразительное искусство Исследование по теме: Спутниковая связь и ее роль в жизни человека
Исследование по теме: Спутниковая связь и ее роль в жизни человека Автоматизированная информационная система для диспетчера УО БГКЛП имени В.Е. Чернышева
Автоматизированная информационная система для диспетчера УО БГКЛП имени В.Е. Чернышева Межпредметная интеграция – необходимое условие современного образования Межпредметная интеграция – необходимое условие совре
Межпредметная интеграция – необходимое условие современного образования Межпредметная интеграция – необходимое условие совре Протезирование пациентов после травм челюстей
Протезирование пациентов после травм челюстей  МОУ «Анаткасинская начальная школа-детский сад» Моргаушский район Исследовательский проект Хвостатые гидростроители
МОУ «Анаткасинская начальная школа-детский сад» Моргаушский район Исследовательский проект Хвостатые гидростроители СТОЛБНЯК (Tetanus) (А35)
СТОЛБНЯК (Tetanus) (А35)  Система знаний о мире (в гипотезах, аксиомах, теоремах, законах, принципах, понятиях, теориях) Система знаний о мире (в гипотезах, ак
Система знаний о мире (в гипотезах, аксиомах, теоремах, законах, принципах, понятиях, теориях) Система знаний о мире (в гипотезах, ак Программирование. Наука управлять
Программирование. Наука управлять Физическая культура в ВУЗе
Физическая культура в ВУЗе Архитектура школы
Архитектура школы Порядок применения электронной компонентной базы иностранного производства в радиоэлектронной аппаратуре для ВВСТ
Порядок применения электронной компонентной базы иностранного производства в радиоэлектронной аппаратуре для ВВСТ ОСНОВНИЙ РЕКЛАМНИЙ ТЕКСТ
ОСНОВНИЙ РЕКЛАМНИЙ ТЕКСТ Исполнение и разучивание духовных кантов как один из видов миссионерского служения
Исполнение и разучивание духовных кантов как один из видов миссионерского служения Расчет на сейсмические воздействия по методике СП 14.13330.2014
Расчет на сейсмические воздействия по методике СП 14.13330.2014 Политические партии и общественные организации
Политические партии и общественные организации Презентация на тему "Личностно-ориентированный и индивидуальный подход в обучении учащихся" - скачать презентации по Педагог
Презентация на тему "Личностно-ориентированный и индивидуальный подход в обучении учащихся" - скачать презентации по Педагог Цветовая палитра интерьера ИМТ
Цветовая палитра интерьера ИМТ ФК Витязь
ФК Витязь Деформационные швы
Деформационные швы Планирование кухни, столовой
Планирование кухни, столовой