Содержание
- 2. Основные понятия математического моделирования Математическая модель - совокупность уравнений и граничных условий, описывающих зависимость выходных величин
- 3. Группы математических моделей установившегося режима (модель статики) отражает функциональную связь между входными и выходными величинами в
- 4. Модели динамики переходный режим - режим функционирования системы описываемый дифференциальным или интегрально-дифференциальным уравнением; установившийся режим -
- 5. Математические модели установившегося и переходного режимов и методы их линеаризации Как уравнения статики, так и уравнения
- 6. Линеаризация уравнений динамики В общем случае при наличии одной выходной (у) и нескольких входных величин (х)
- 7. Линеаризация уравнений статики Уравнения статики элементов (систем) автоматического управления, как правило, нелинейные и могут быть представлены
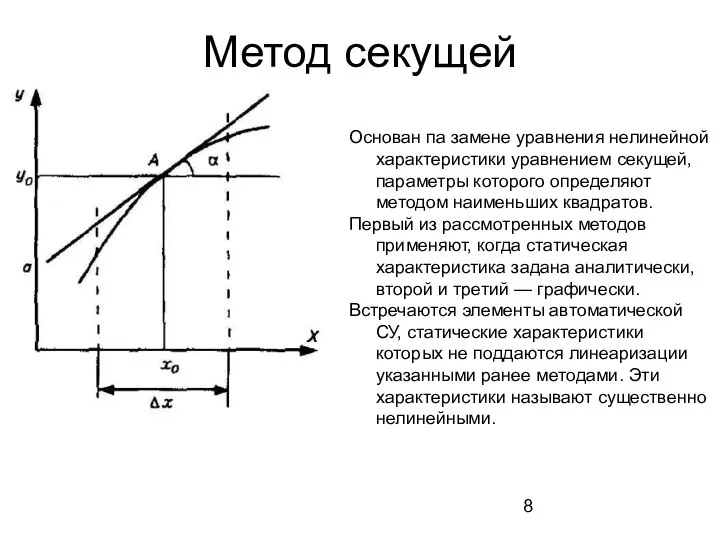
- 8. Метод секущей Основан па замене уравнения нелинейной характеристики уравнением секущей, параметры которого определяют методом наименьших квадратов.
- 9. Аналитический метод построения математической модели Дифференциальные уравнения простых элементов можно составить, используя закономерности протекающих в них
- 10. Экспериментальные методы построения математической модели В практике синтеза автоматических СУ технологическими процессами сельскохозяйственного производства используют два
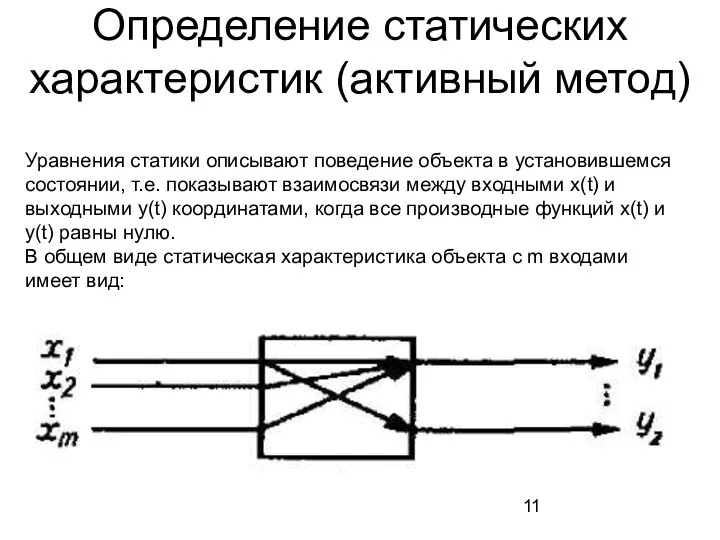
- 11. Определение статических характеристик (активный метод) Уравнения статики описывают поведение объекта в установившемся состоянии, т.е. показывают взаимосвязи
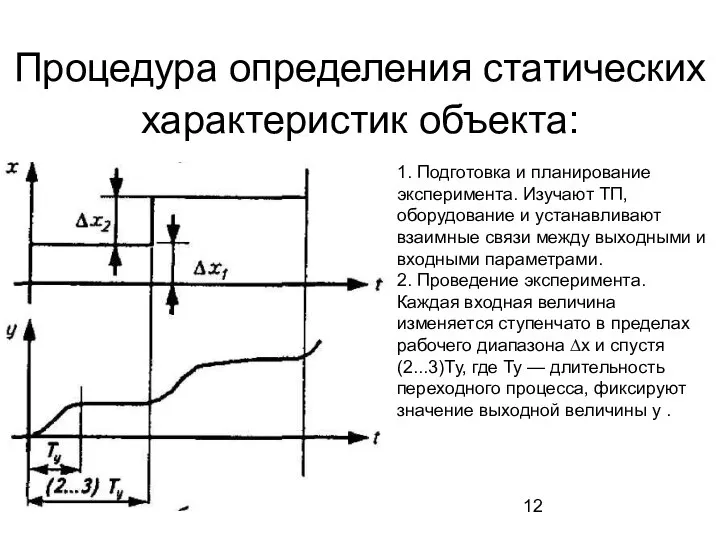
- 12. Процедура определения статических характеристик объекта: 1. Подготовка и планирование эксперимента. Изучают ТП, оборудование и устанавливают взаимные
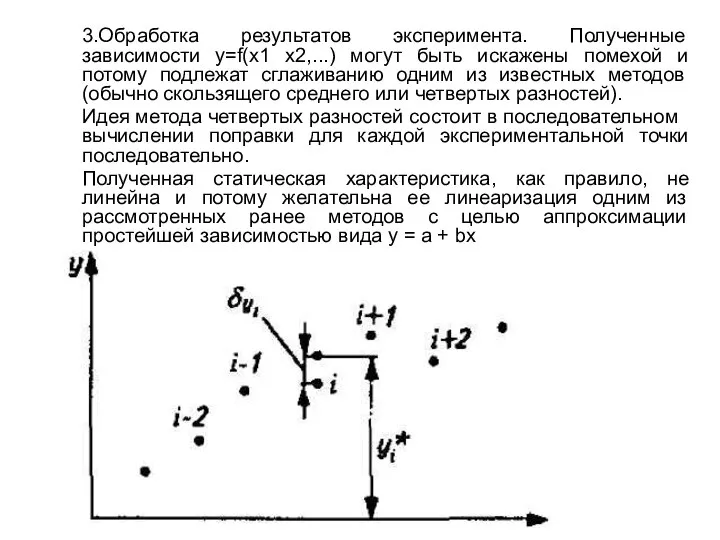
- 13. 3.Обработка результатов эксперимента. Полученные зависимости у=f(x1 х2,...) могут быть искажены помехой и потому подлежат сглаживанию одним
- 14. Определение статических характеристик (пассивный метод). Стохастические (случайные) изменения выходных величин нормально функционирующего объекта автоматизации обусловлены как
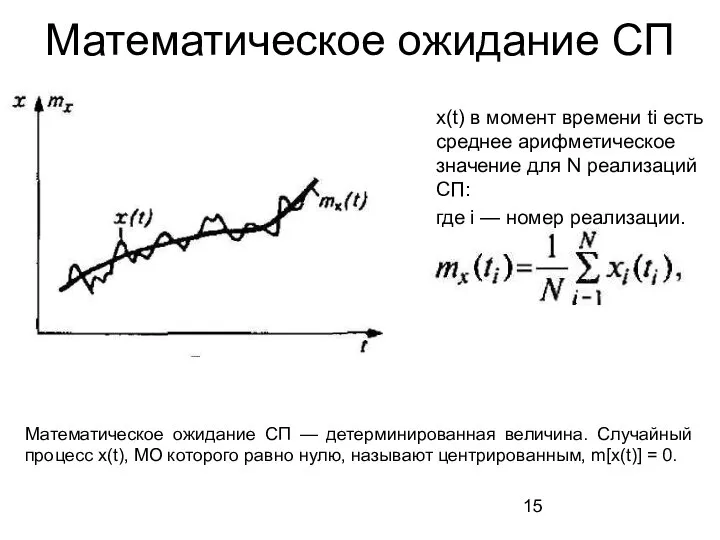
- 15. Математическое ожидание СП x(t) в момент времени ti есть среднее арифметическое значение для N реализаций СП:
- 16. Дисперсия Интенсивность отклонения СП от МО. Ее определяют как среднее значение квадрата колебаний центрированного СП: Дисперсия
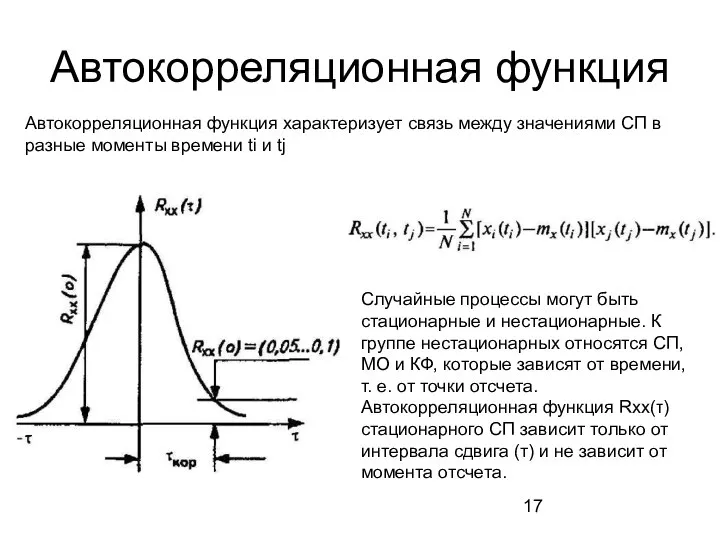
- 17. Автокорреляционная функция Автокорреляционная функция характеризует связь между значениями СП в разные моменты времени ti и tj
- 19. Скачать презентацию










 Экосистемы
Экосистемы Управление деловой карьерой в организации
Управление деловой карьерой в организации Политология, как наука о политике и ее взаимоотношениях с обществом
Политология, как наука о политике и ее взаимоотношениях с обществом Как жить в мире с родителями? Классный час
Как жить в мире с родителями? Классный час Исаак Ильич Левитан (1860-1900) Работу выполнил Тихачев Вячеслав ученик 5 «Б» класса МОУ лицея №10 Г. Советска
Исаак Ильич Левитан (1860-1900) Работу выполнил Тихачев Вячеслав ученик 5 «Б» класса МОУ лицея №10 Г. Советска Учебный план 1 класса на 2010-2011учебный год ГОУ СОШ с УИОП г.Белой Холуницы Кировской области
Учебный план 1 класса на 2010-2011учебный год ГОУ СОШ с УИОП г.Белой Холуницы Кировской области Аттестационная работа. Методическая разработка по выполнению исследовательской работы «Секреты колыбельной песни»
Аттестационная работа. Методическая разработка по выполнению исследовательской работы «Секреты колыбельной песни» Туризм. Грузия
Туризм. Грузия Личность Психопатии Олигофрения
Личность Психопатии Олигофрения Pancakes week, Maslenitsa
Pancakes week, Maslenitsa Облачные технологии как информационные сервисы Интернет
Облачные технологии как информационные сервисы Интернет Объектно-ориентированное программирование. Языки C++ и C#
Объектно-ориентированное программирование. Языки C++ и C# Кенигсберг – это крепость? Шумилина В.А.
Кенигсберг – это крепость? Шумилина В.А. Методы изучения наследственности человека
Методы изучения наследственности человека  Дипломатия и демократия. Дипломатия и переговоры
Дипломатия и демократия. Дипломатия и переговоры Фокина Л. П. Тренажёр-раскраска СЛОВАРНЫЕ СЛОВА. Часть 2 - презентация для начальной школы
Фокина Л. П. Тренажёр-раскраска СЛОВАРНЫЕ СЛОВА. Часть 2 - презентация для начальной школы Александр Карелин
Александр Карелин Презентация "Деревянне зодчество Руси" - скачать презентации по МХК
Презентация "Деревянне зодчество Руси" - скачать презентации по МХК Український національний костюм
Український національний костюм Классификация деловых культур по Р. Гестеланду
Классификация деловых культур по Р. Гестеланду Развитие натуралистических умений учащихся средствами изобразительного искусства
Развитие натуралистических умений учащихся средствами изобразительного искусства Презентация "Костюм xviii века" - скачать презентации по МХК
Презентация "Костюм xviii века" - скачать презентации по МХК “ҚАЗФОСФАТ” ЖШС
“ҚАЗФОСФАТ” ЖШС Современные перспективные технологии
Современные перспективные технологии Рекурсивные функции языка CLIPS
Рекурсивные функции языка CLIPS IT – Скорая. Организация по ремонту компьютеров
IT – Скорая. Организация по ремонту компьютеров Тренинг "Сплочение коллектива". Познание стран мира
Тренинг "Сплочение коллектива". Познание стран мира ЦИКЛИЧЕСКИЕ НУКЛЕОТИДЫ В РОЛИ ВТОРИЧНЫХ ПОСРЕДНИКОВ
ЦИКЛИЧЕСКИЕ НУКЛЕОТИДЫ В РОЛИ ВТОРИЧНЫХ ПОСРЕДНИКОВ