Содержание
- 2. В момент прохождения частицы с высокой энергией счетчик воспринимает сигнал с усилителя сигнала УС и пересчитывает
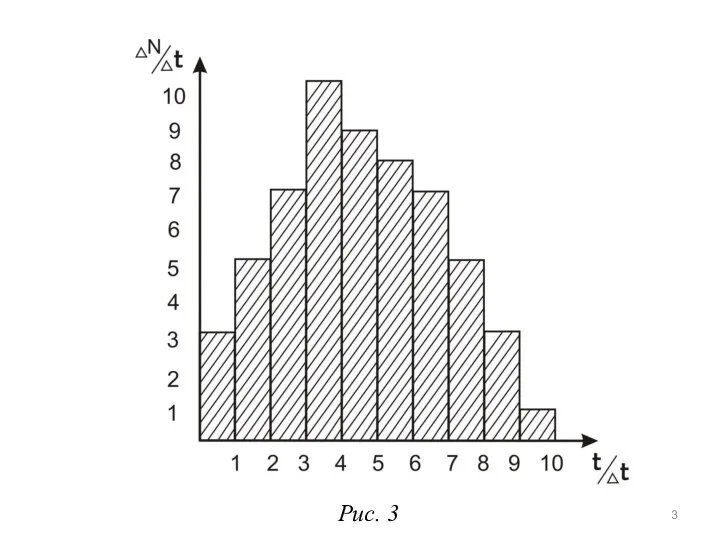
- 3. Рис. 3
- 4. График - называется дискретной функцией распределения (математики называют его гистограммой). Она показывает: какое число быстрых частиц
- 5. Если сложить площадь всех столбиков на графике: - полное число частиц, пролетевших через счетчик (1) N=3+5+7+10+9+8+7+5+3+1=58
- 6. Функция (2) показывает какая доля частиц пролетает через счетчик в момент времени от до . В
- 7. Она равна: , (4) где - нормированная на число частиц, непрерывная функция распределения по значениям величины
- 8. то вероятность, выраженная через долю частиц, имеет вид: (6) Отсюда, количество молекул , для которых величина
- 9. 3.2. Функции распределения молекул по скоростям в газе. Молекулы газа, находящегося в равновесии движутся с самыми
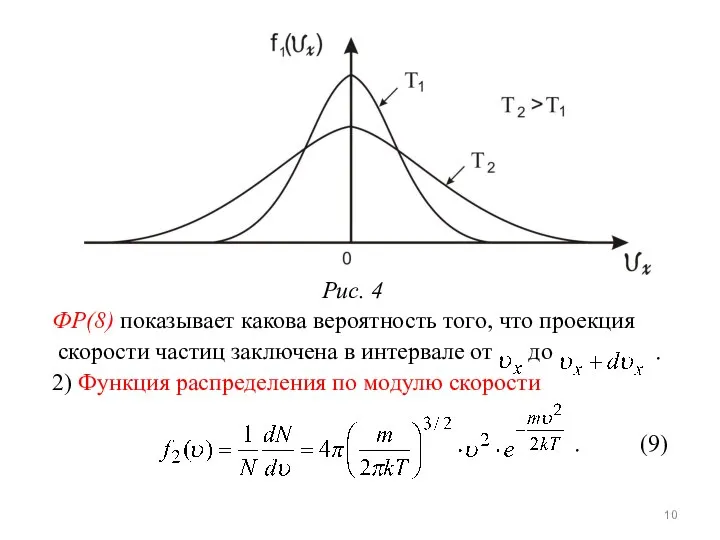
- 10. Рис. 4 ФР(8) показывает какова вероятность того, что проекция скорости частиц заключена в интервале от до
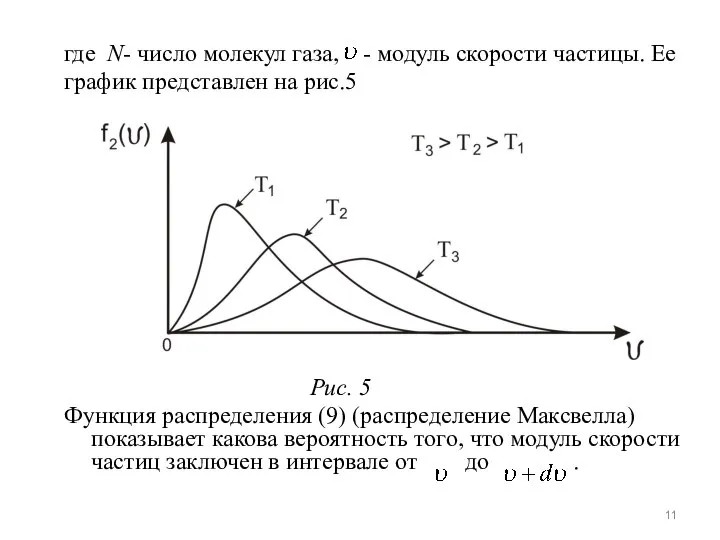
- 11. где N- число молекул газа, - модуль скорости частицы. Ее график представлен на рис.5 Рис. 5
- 12. Различие законов связано с тем, что - указывает на равновесность распределения молекул по направлениям в пространстве:
- 13. откуда - наиболее вероятная скорость. 2. Максимальное значение функции . При - максимум убывает с ростом
- 14. 4. ГАЗЫ В СИЛОВОМ ПОЛЕ 4.1 БАРОМЕТРИЧЕСКАЯ ФОРМУЛА Рассмотрим идеальный газ, находящийся в однородном поле силы
- 15. Выражая плотность из уравнения Менделеева-Клапейрона и подставляя её в (1), получим (2). Интегрирование приводит к соотношению
- 18. Скачать презентацию












 Architecture for dummies
Architecture for dummies Функции И+ПРГ C \ С++
Функции И+ПРГ C \ С++ Терминология ДВС- синдрома «синдром диссеминированного внутрисосудистого свертывания крови» «тромбогеморрагический синдром»
Терминология ДВС- синдрома «синдром диссеминированного внутрисосудистого свертывания крови» «тромбогеморрагический синдром»  Презентация____
Презентация____ Синтез систем автоматического управления
Синтез систем автоматического управления Легкая атлетика
Легкая атлетика Понятие и виды государственной службы
Понятие и виды государственной службы Виды энергий
Виды энергий Русские фамилии тюркского происхождения
Русские фамилии тюркского происхождения Витаминный калейдоскоп - презентация для начальной школы_
Витаминный калейдоскоп - презентация для начальной школы_ Оси и валы
Оси и валы Аттестационная работа. Проектная работа «ГородОК №45. Система голосования»
Аттестационная работа. Проектная работа «ГородОК №45. Система голосования» Програмування та прикладні інформаційні системи
Програмування та прикладні інформаційні системи Воспаление
Воспаление  Организация работ по диагностированию, техническому обслуживанию автомобиля Renault Logan. Ремонт системы освещения
Организация работ по диагностированию, техническому обслуживанию автомобиля Renault Logan. Ремонт системы освещения Презентация Предложение. Эастичность
Презентация Предложение. Эастичность Жизнь земледельцев на Руси
Жизнь земледельцев на Руси Назначение судебных экспертиз оперуполномоченным уголовного розыска при производстве дознания
Назначение судебных экспертиз оперуполномоченным уголовного розыска при производстве дознания Сурский лед - родина чемпионов. Зарождение пензенского хоккея
Сурский лед - родина чемпионов. Зарождение пензенского хоккея Ostern in Deutschland
Ostern in Deutschland 58ad82fefee7471ea09dd60cc1439c9a
58ad82fefee7471ea09dd60cc1439c9a Спортивные игры. Волейбол
Спортивные игры. Волейбол Всероссийский марафон "С немецким ты знаешь больше"
Всероссийский марафон "С немецким ты знаешь больше" Введение в XML
Введение в XML Фестиваль-ярмарка "Панинский рождественский гусь"
Фестиваль-ярмарка "Панинский рождественский гусь" PL泵 PL泵简介 PL泵泵体结构和调整
PL泵 PL泵简介 PL泵泵体结构和调整 Основные типы структурных схем радиоприемных устройств
Основные типы структурных схем радиоприемных устройств Религиозная карта мира
Религиозная карта мира