Содержание
- 2. Квантовомеханическое описание Задача: найти и охарактеризовать все состояния, в которых частица может быть обнаружена СОСТОЯНИЕ ВЕКТОР
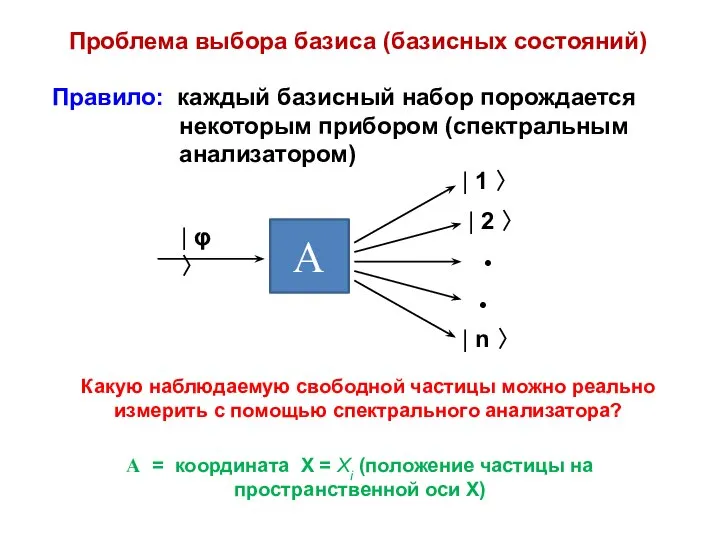
- 3. Проблема выбора базиса (базисных состояний) Правило: каждый базисный набор порождается некоторым прибором (спектральным анализатором) Какую наблюдаемую
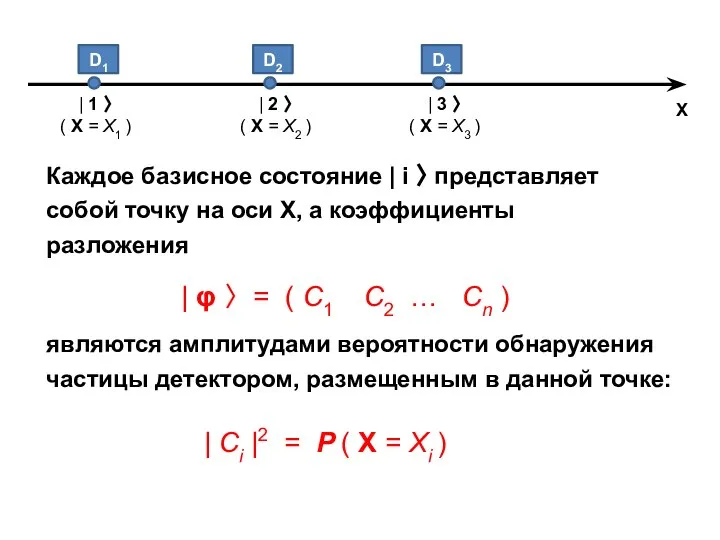
- 4. Каждое базисное состояние | i 〉 представляет собой точку на оси Х, а коэффициенты разложения |
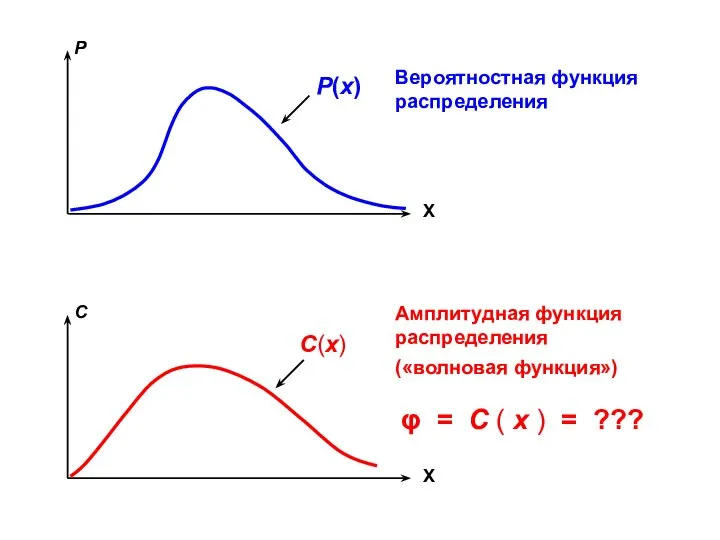
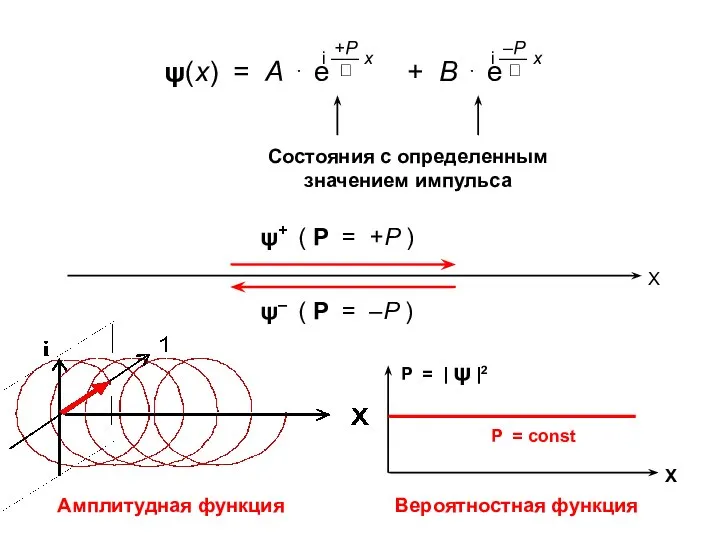
- 5. X P X C P(x) C(x) Вероятностная функция распределения Амплитудная функция распределения («волновая функция») φ =
- 6. Задача: найти явный вид волновых функций, описывающих все возможные состояния свободной частицы: φ(x, t) = ???
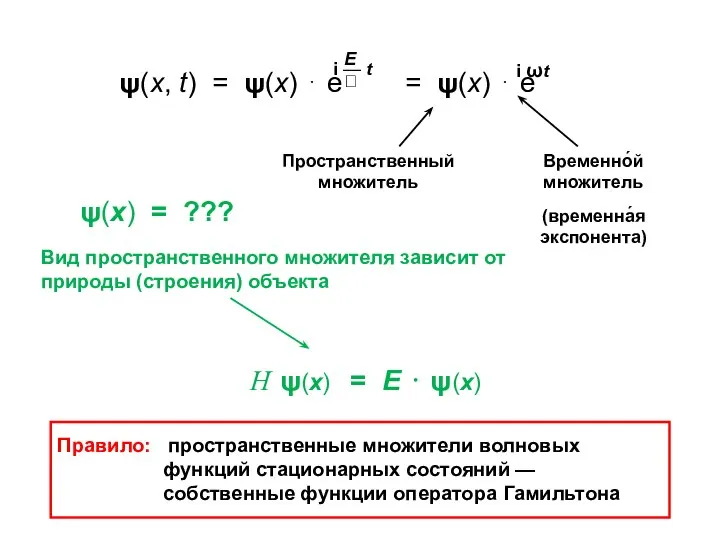
- 7. Правило: собственные функции всякого оператора образуют базисный набор: Е — энергия стационарного состояния (собственное значение оператора
- 8. Проверка ( i ⋅ i = – 1 )
- 9. Пространственный множитель Временно́й множитель (временна́я экспонента) ψ(x) = ??? Вид пространственного множителя зависит от природы (строения)
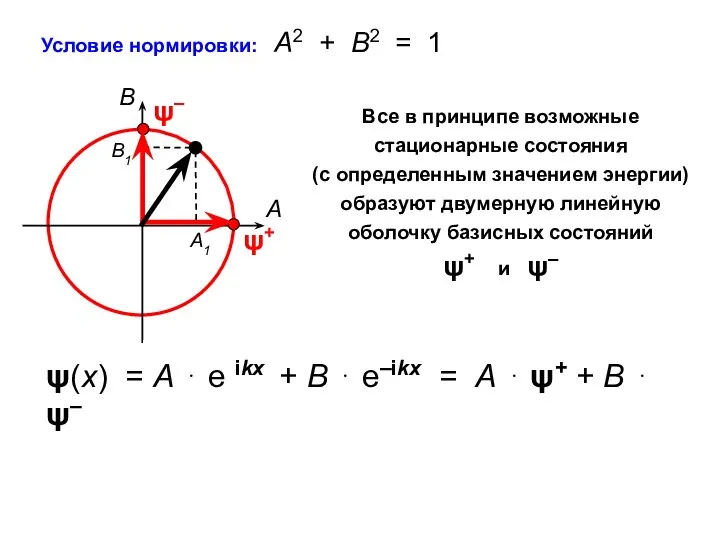
- 10. ψ+(х) = е ikx и ψ– (х) = e–ikx ψ(х) = А ⋅ е ikx +
- 11. Условие нормировки: А2 + В2 = 1 Все в принципе возможные стационарные состояния (с определенным значением
- 12. Чтобы найти константу k, продифференцируем дважды любое частное решение: d 2 (еikx)/dx2 = –k2(еikx) или d
- 13. Амплитудная функция Вероятностная функция
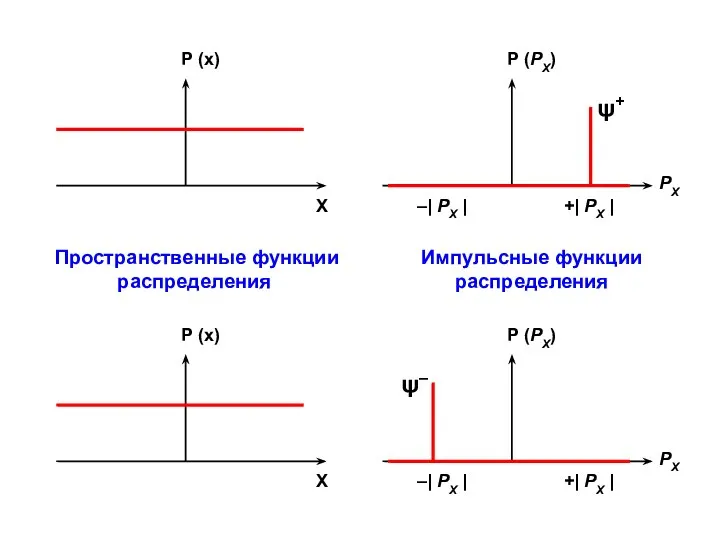
- 14. Пространственные функции распределения Импульсные функции распределения
- 15. Наблюдаемые Х (координата) и РХ (импульс) связаны между собой соотношением неопределенности Гейзенберга: если величина одной из
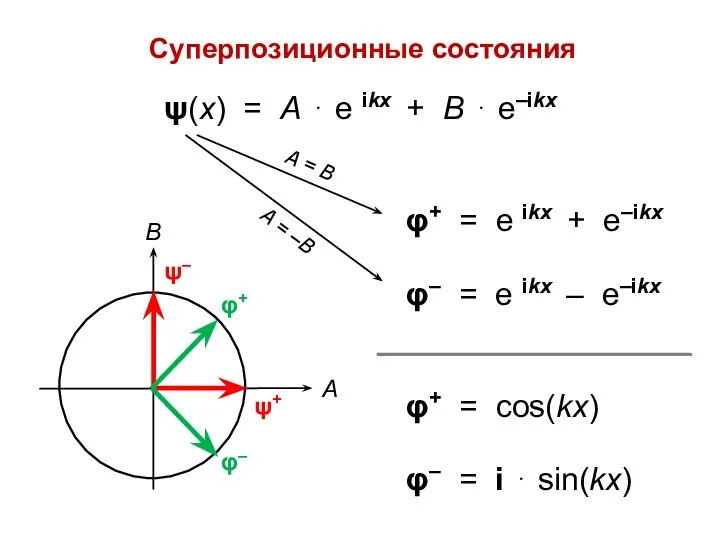
- 16. Суперпозиционные состояния ψ(х) = А ⋅ е ikx + В ⋅ e–ikx
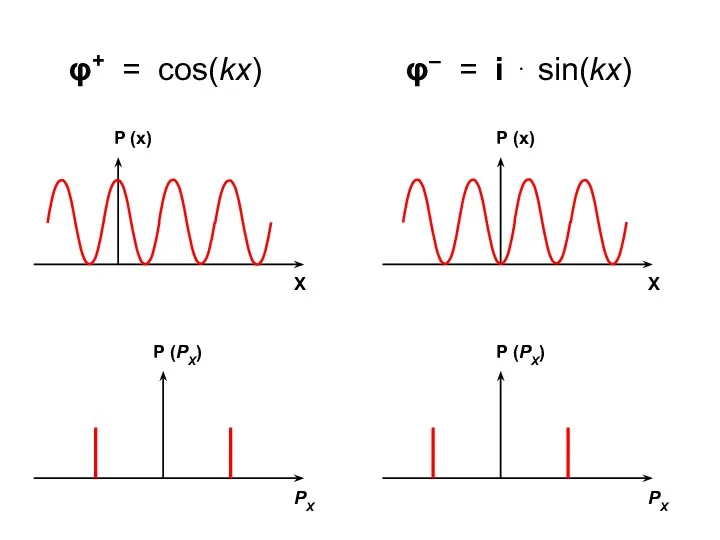
- 17. φ+ = cos(kx) φ– = i ⋅ sin(kx)
- 19. Скачать презентацию







 Теория и практика решения кейсов по корпоративному праву
Теория и практика решения кейсов по корпоративному праву Лидерство. Стили лидерства
Лидерство. Стили лидерства Истинное поклонение. Причина поклонения. Что такое поклонение
Истинное поклонение. Причина поклонения. Что такое поклонение Не отрывая карандаша - презентация для начальной школы_
Не отрывая карандаша - презентация для начальной школы_ День Збройних сил України
День Збройних сил України Аттестационная работа. Создание творческого проекта «Кукла-мотанка»
Аттестационная работа. Создание творческого проекта «Кукла-мотанка» Древнегреческий театр
Древнегреческий театр Трансформатор. Режимы работы трансформатора
Трансформатор. Режимы работы трансформатора Тема: «Влияние родителей на отношение подростков к курению»
Тема: «Влияние родителей на отношение подростков к курению» Иван Грозный Цель: узнать о личности царя Ивана Грозного; показать его историческую роль в Российском государстве.
Иван Грозный Цель: узнать о личности царя Ивана Грозного; показать его историческую роль в Российском государстве. Макроэкономика Основы макроэкономического анализа. Подготовила: студентка 21 Э группы Тришмак Л. Проверил: Грубов А. П.
Макроэкономика Основы макроэкономического анализа. Подготовила: студентка 21 Э группы Тришмак Л. Проверил: Грубов А. П. Окончание предварительного расследования
Окончание предварительного расследования Как новые медиа трансформируют общество
Как новые медиа трансформируют общество Организация С#-системы ввода-вывода
Организация С#-системы ввода-вывода Антуан де Сент-Экзюпери
Антуан де Сент-Экзюпери Правовые системы и правовые семьи
Правовые системы и правовые семьи Буддизм. Отношение к природе
Буддизм. Отношение к природе Создание планово-высотного обоснования и съемка карьера тахеометром Nikon NPL 332
Создание планово-высотного обоснования и съемка карьера тахеометром Nikon NPL 332 Обзор СУБД (MS SQL Server, Oracle Database, MS Access, MS Visual FoxPro, Progress, MySQL, Postgres
Обзор СУБД (MS SQL Server, Oracle Database, MS Access, MS Visual FoxPro, Progress, MySQL, Postgres Теоремы о функциях, непрерывных на отрезке
Теоремы о функциях, непрерывных на отрезке Контрактные цены как база определения таможенной стоимости и таможенных платежей Выполнила Хропина Ольга
Контрактные цены как база определения таможенной стоимости и таможенных платежей Выполнила Хропина Ольга Подготовка к ЕГЭ Задание А12
Подготовка к ЕГЭ Задание А12 Безпека в інтернеті!
Безпека в інтернеті! Конденсаторы
Конденсаторы Первый поход Ерофея Хабарова
Первый поход Ерофея Хабарова Дисциплина профессионального цикла для студентов, обучающихся по магистерским программам
Дисциплина профессионального цикла для студентов, обучающихся по магистерским программам  5 Изложение 489
5 Изложение 489 Самое дорогое - презентация для начальной школы
Самое дорогое - презентация для начальной школы