Содержание
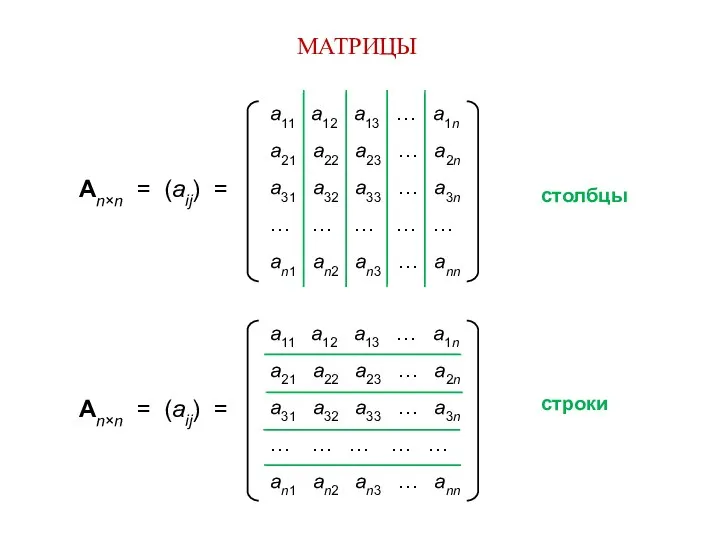
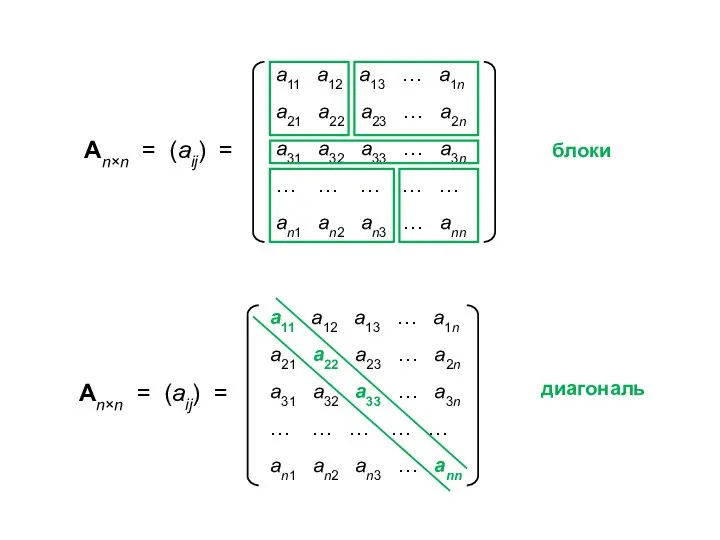
- 2. МАТРИЦЫ
- 4. Характеристики матриц 1. След Sp = a11 + a22 + … + ann = ∑ aii
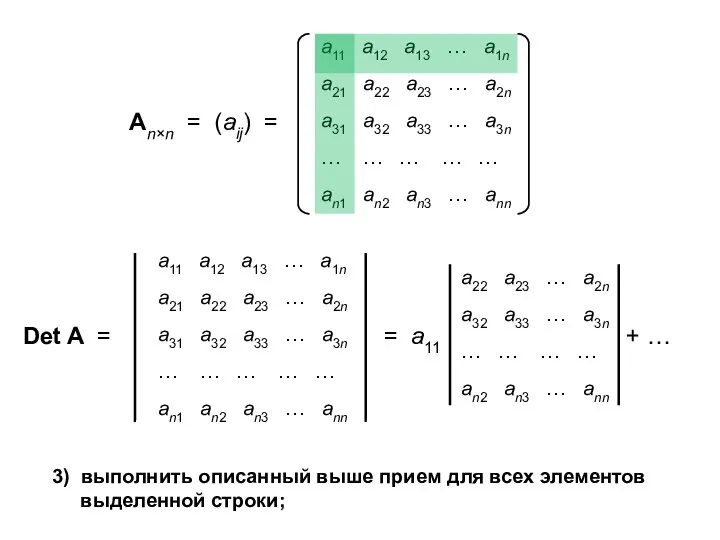
- 5. 3) выполнить описанный выше прием для всех элементов выделенной строки;
- 6. 4) каждое произведение дополнительно умножить на (–1)i+j, где i и j — индексы элемента выделенной строки.
- 7. 5) применить описанную процедуру ко всем определителям с размерностью (n – 1), в результате чего каждый
- 8. Пример = 2 ⋅ (5 ⋅ 5 – 7 ⋅ 1) – 4 ⋅ (3 ⋅
- 9. Пример = 2 ⋅ (5 ⋅ 5 + 7 ⋅ 1) + 4 ⋅ (3 ⋅
- 10. Операции над матрицами 1. Сложение матриц А + В = С 2. Умножение матрицы на число
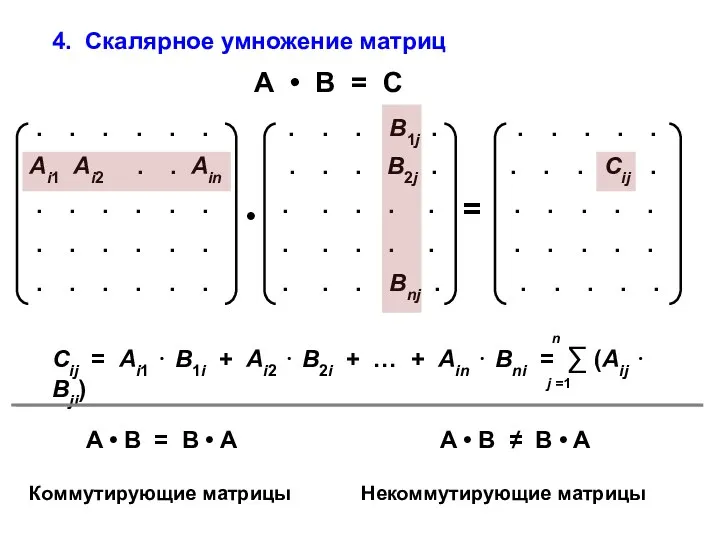
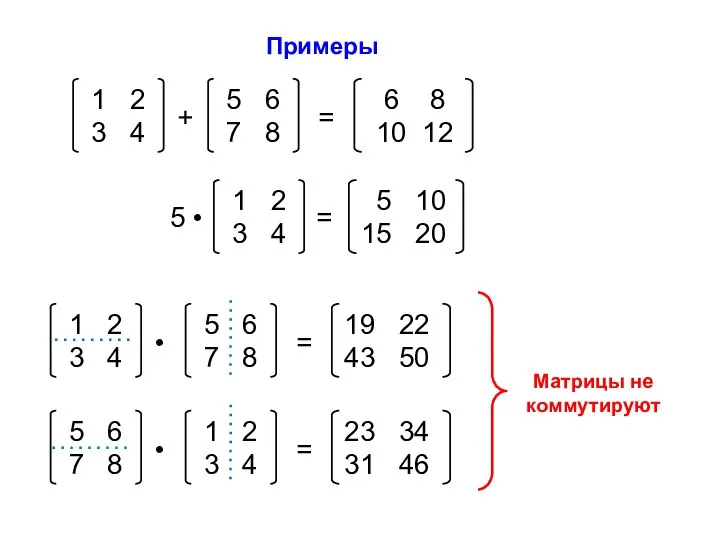
- 11. 4. Скалярное умножение матриц А • В = С Коммутирующие матрицы Некоммутирующие матрицы
- 12. Примеры
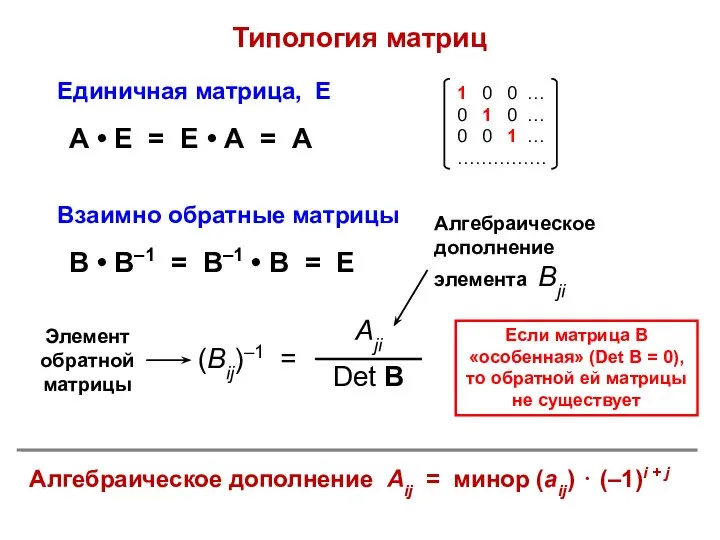
- 13. Типология матриц Взаимно обратные матрицы В • В–1 = В–1 • В = Е Если матрица
- 14. Пример А11 = +4 А12 = –3 А21 = –2 А22 = +1 (В11)–1 = +4/–2
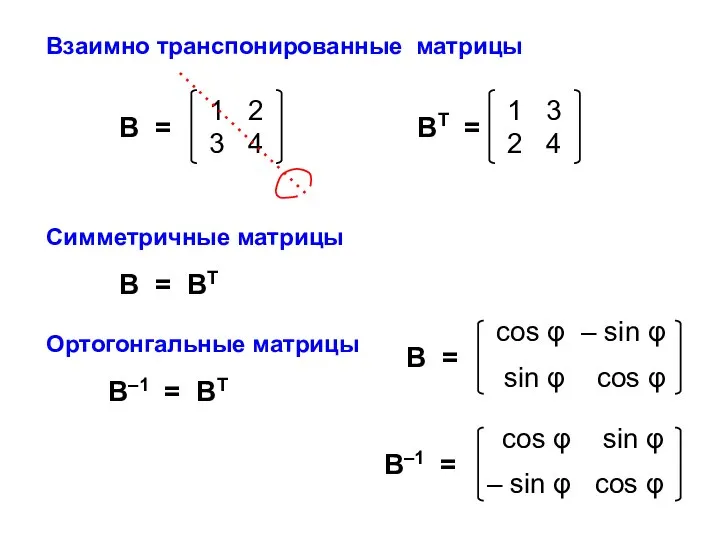
- 15. Взаимно транспонированные матрицы Симметричные матрицы В–1 = ВТ В = ВТ Ортогонгальные матрицы
- 16. Комплексно сопряженные матрицы В = В+ Самосопряженные (эрмитовы) матрицы Эрмитово сопряженные матрицы В–1 = В+ Унитарные
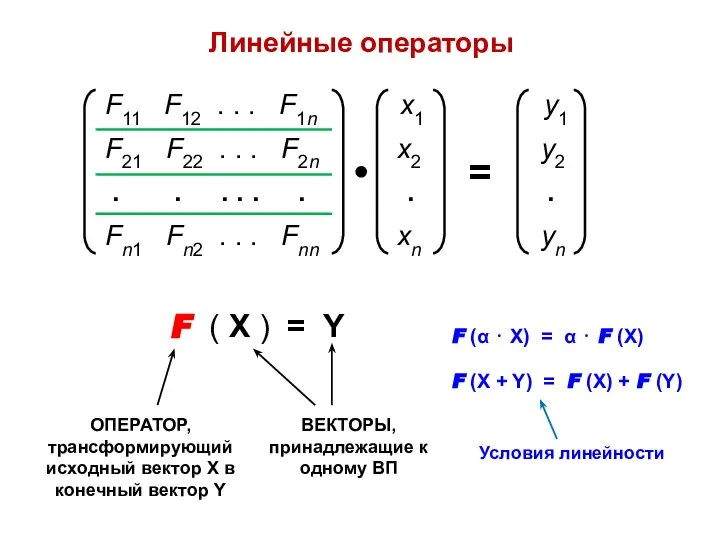
- 17. Линейные операторы F ( X ) = Y
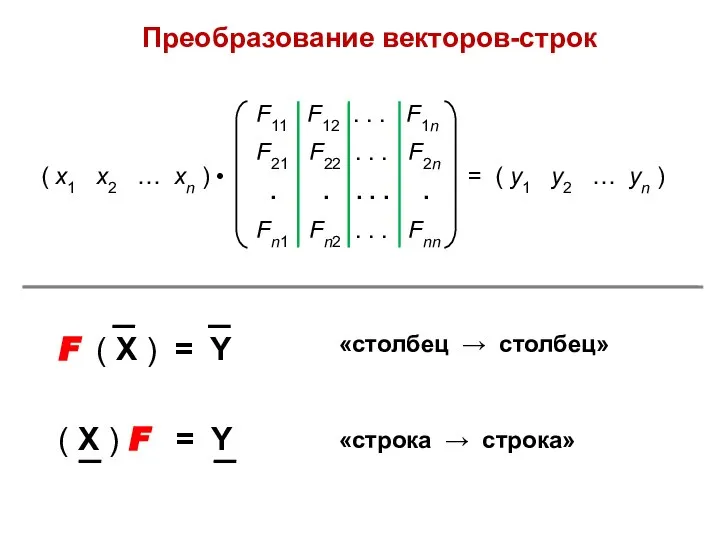
- 18. Преобразование векторов-строк
- 19. 1. Любая квадратная матрица может выступать в роли оператора 2. Любой оператор может быть изображен в
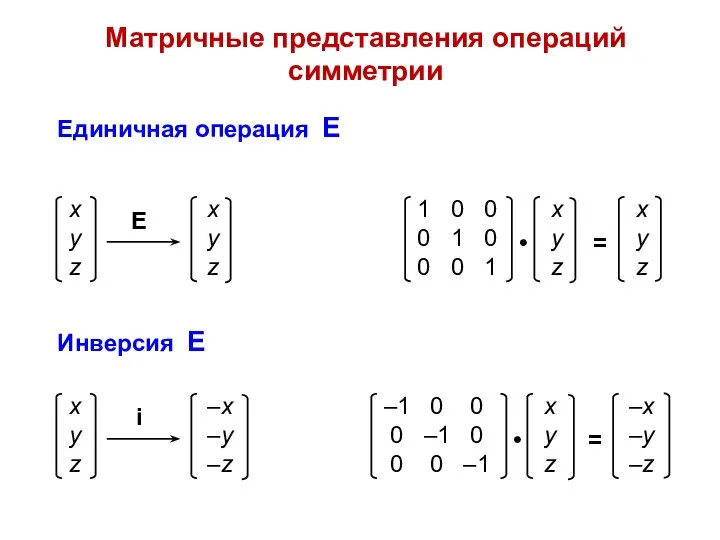
- 20. Матричные представления операций симметрии Единичная операция E Инверсия E
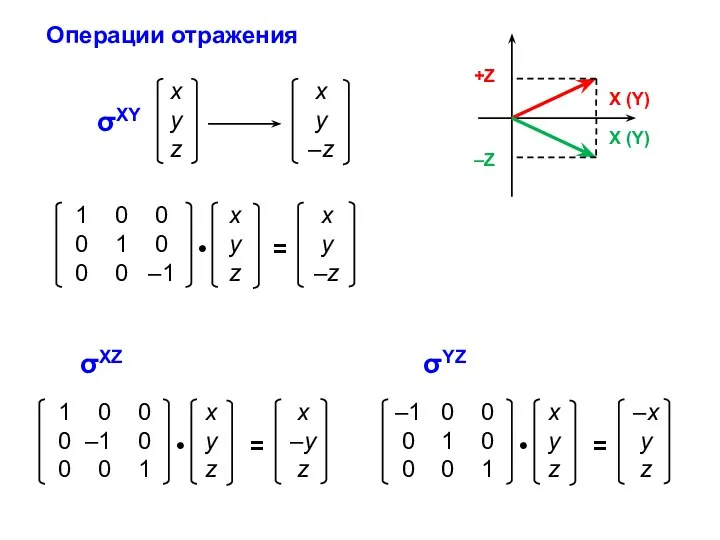
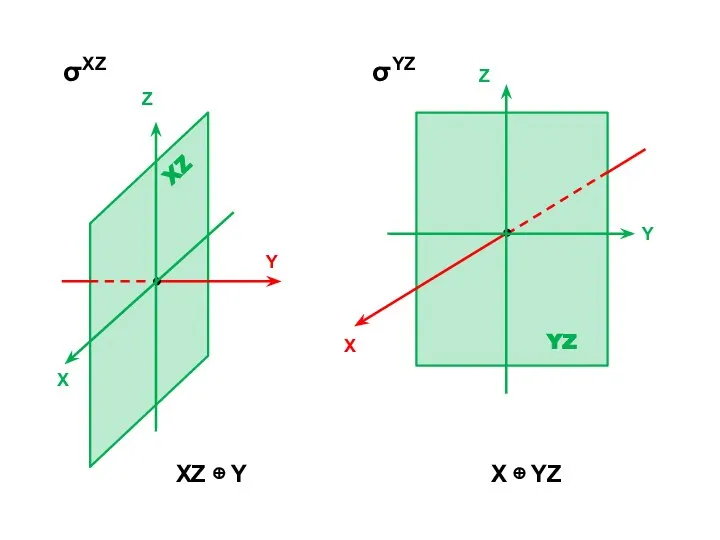
- 21. σXY Операции отражения
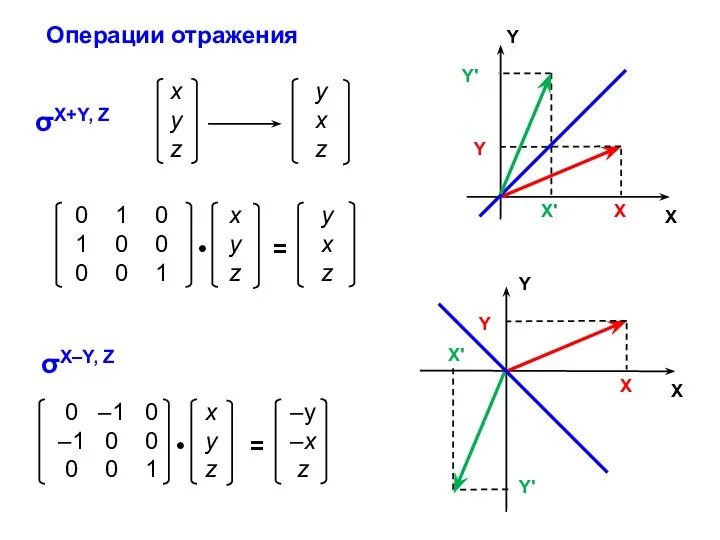
- 22. σX+Y, Z Операции отражения
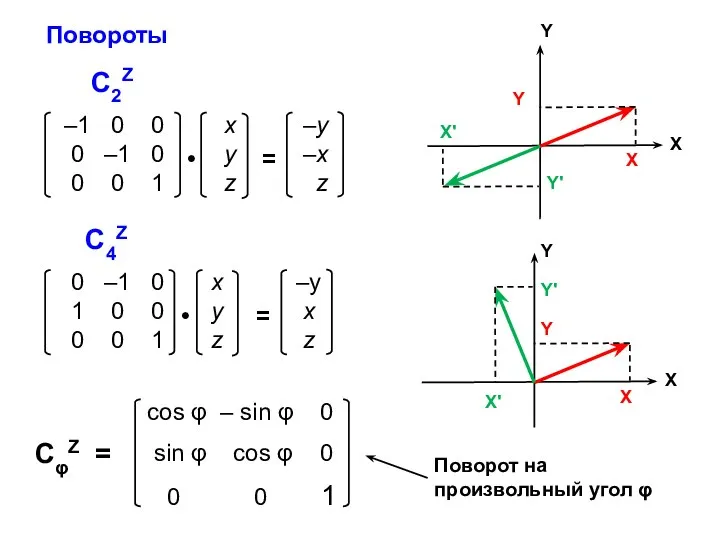
- 23. С2Z Повороты
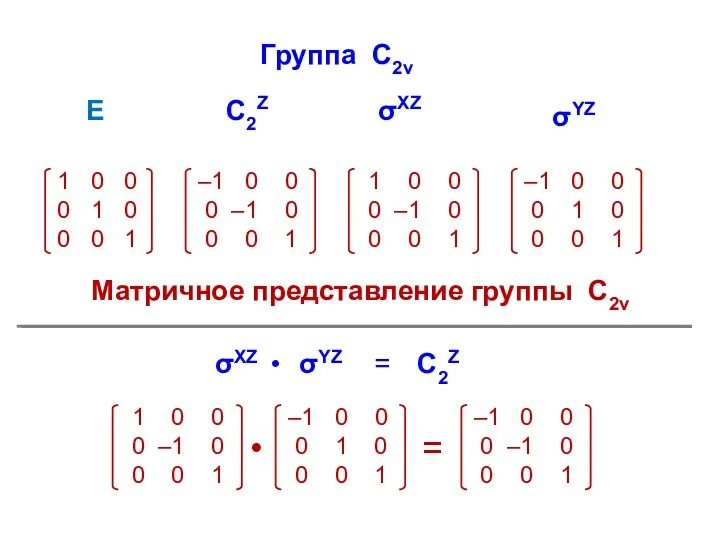
- 24. Матричное представление группы С2v E C2Z Группа С2v σXZ σYZ
- 25. Домашнее задание Задача 3.1. Установить, коммутируют ли между собой заданные операции симметрии, найти коммутатор. 1) найти
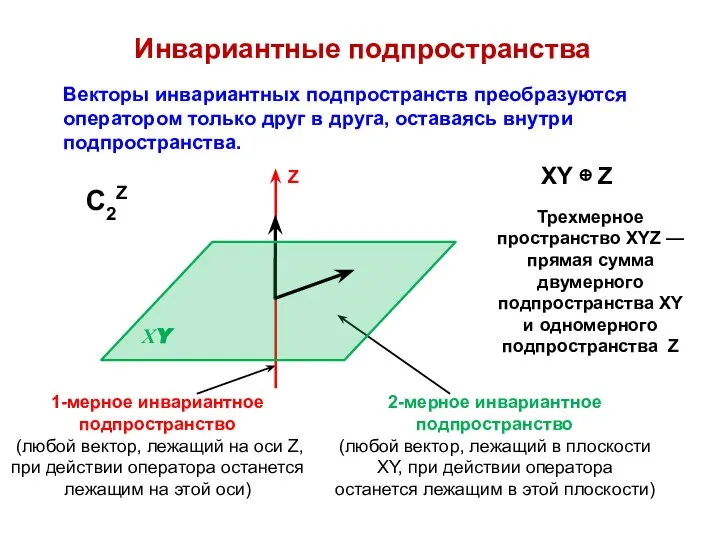
- 26. Инвариантные подпространства Векторы инвариантных подпространств преобразуются оператором только друг в друга, оставаясь внутри подпространства. C2Z 2-мерное
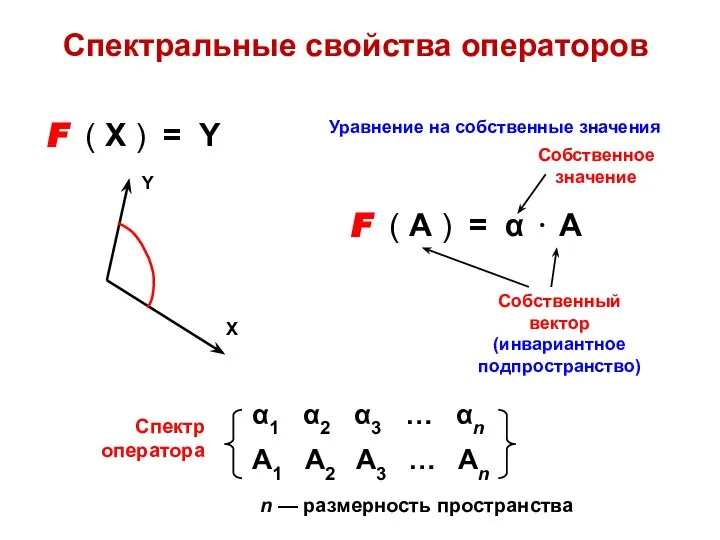
- 28. Спектральные свойства операторов F ( X ) = Y F ( А ) = α ⋅
- 29. F ( А ) = α ⋅ А F11 ⋅ а1 + F12 ⋅ а2 +
- 30. (F11 – α) ⋅ а1 + F12 ⋅ а2 + . . . + F1n ⋅
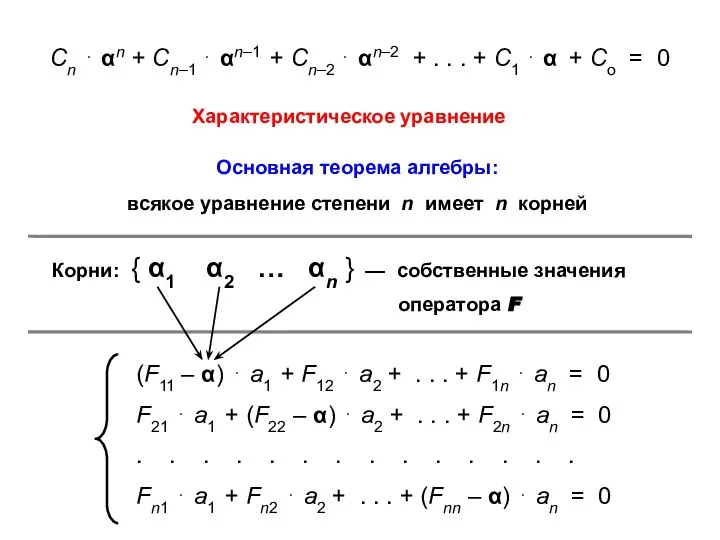
- 31. Сn ⋅ αn + Сn–1 ⋅ αn–1 + Сn–2 ⋅ αn–2 + . . . +
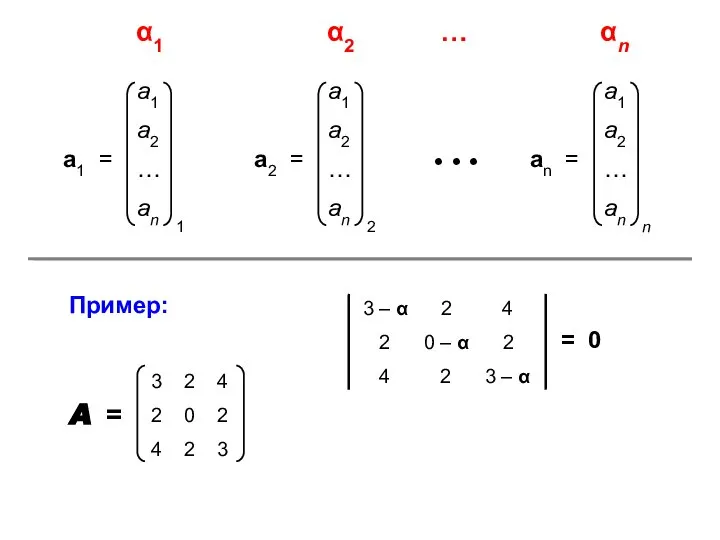
- 32. α1 α2 … αn • • • Пример:
- 33. Det = (3 – α) ⋅ (0 – α) ⋅ (3 – α) + 2 ⋅
- 34. α1 = 8 Вычитая третье уравнение из первого, получим: –9x + 9z = 0 или x
- 35. α = –1 4 х + 2 y + 4 z = 0 2 x +
- 36. Первый базисный вектор можно выбрать произвольно. Положим, например, х = 0 и у = 1. Тогда
- 37. α1 = 8 α2 = α2 = –1 Проверка = = (+8) ⋅ А (а1) =
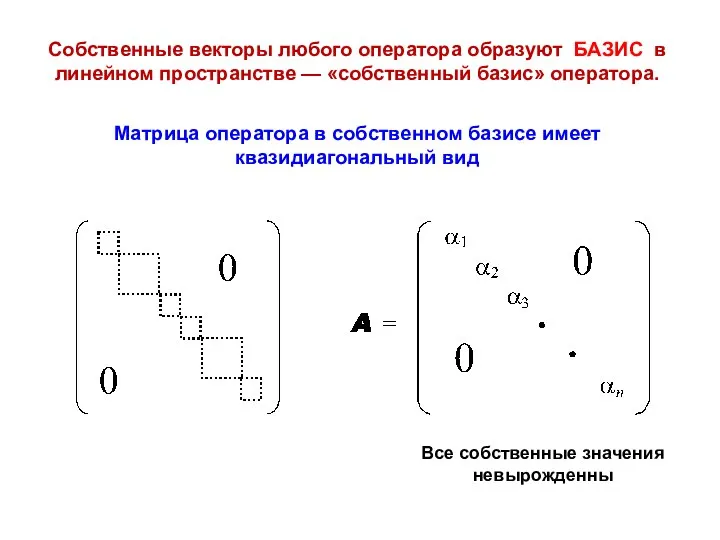
- 38. Собственные векторы любого оператора образуют БАЗИС в линейном пространстве — «собственный базис» оператора. Матрица оператора в
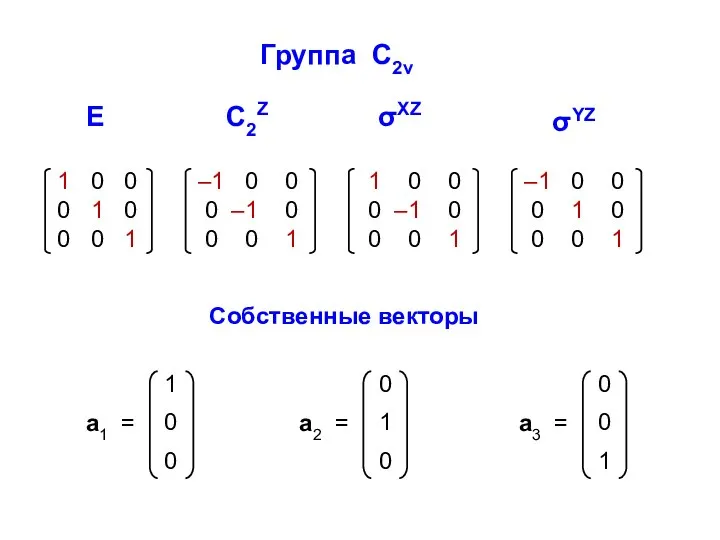
- 39. E C2Z Группа С2v σXZ σYZ Собственные векторы
- 41. Скачать презентацию












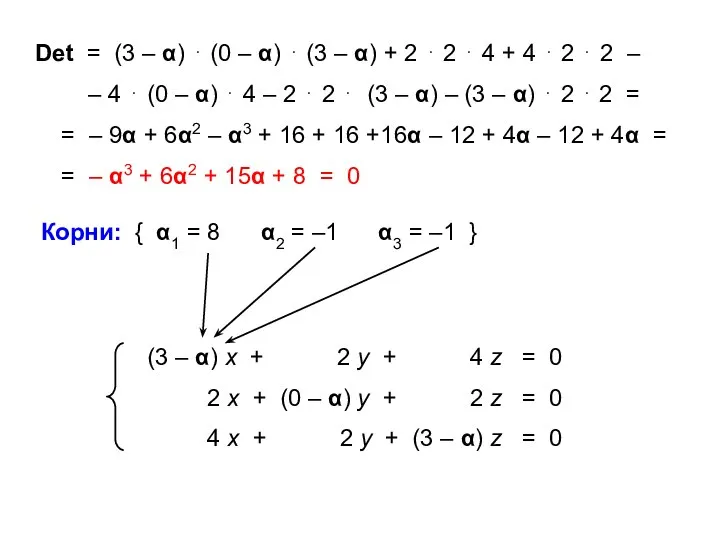




 РОДНОЙ ЯЗЫК ПРАКТИКА ПРЕПОДАВАНИЯ 16.09.19
РОДНОЙ ЯЗЫК ПРАКТИКА ПРЕПОДАВАНИЯ 16.09.19 Гимнастические упражнения как основной способ профилактики заболеваний у детей школьного возраста (11-13 лет)
Гимнастические упражнения как основной способ профилактики заболеваний у детей школьного возраста (11-13 лет) Зачем учить китайский
Зачем учить китайский Профессиональное обучение обучающихся на базе ГПОУ «МЖТ
Профессиональное обучение обучающихся на базе ГПОУ «МЖТ С. Хантингтон «Столкновение цивилизаций». Бжезинский «Великая шахматная доска». А. Богатуров «Великие державы на Тихом океане»
С. Хантингтон «Столкновение цивилизаций». Бжезинский «Великая шахматная доска». А. Богатуров «Великие державы на Тихом океане» ветр оспа история
ветр оспа история Креативные разработки: Слоган как инструмент брендинга
Креативные разработки: Слоган как инструмент брендинга Возрождение традиционного вепсского ремесла - ткачества
Возрождение традиционного вепсского ремесла - ткачества Слайдовая презентация «Зелёная аптека» Выполнила ученица 3 класса МОУ «Безрукавская СОШ» Слонова Анастасия_
Слайдовая презентация «Зелёная аптека» Выполнила ученица 3 класса МОУ «Безрукавская СОШ» Слонова Анастасия_ Теоретические и практические вопросы назначения наказания по совокупности преступлений
Теоретические и практические вопросы назначения наказания по совокупности преступлений Чертежи предметов с использованием геометрических построений
Чертежи предметов с использованием геометрических построений Порты ввода\вывода микроконтроллеров серии AVR. Внешние прерывания
Порты ввода\вывода микроконтроллеров серии AVR. Внешние прерывания Правила проведения соревнований «Формула будущего». Юношеские классы спортивных мотолодок
Правила проведения соревнований «Формула будущего». Юношеские классы спортивных мотолодок Алгоритм выполнения задания А27 (Информационная обработка письменных текстов различных стилей и жанров)
Алгоритм выполнения задания А27 (Информационная обработка письменных текстов различных стилей и жанров) Таблица умножения и деления на 4 Технологический приём анимированная сорбонка
Таблица умножения и деления на 4 Технологический приём анимированная сорбонка Президент Российской Федерации
Президент Российской Федерации Презентация "Презентация проекта" - скачать презентации по Экономике
Презентация "Презентация проекта" - скачать презентации по Экономике ВИЧ – инфекция и нейросифилис
ВИЧ – инфекция и нейросифилис Инвалидность. Получение инвалидности
Инвалидность. Получение инвалидности Русская культура 16-17 веков
Русская культура 16-17 веков Визуальная диагностика рахита Выполнила 307 ОМ Қойшыманова. А Проверила Қожахметова .Ж.Ж
Визуальная диагностика рахита Выполнила 307 ОМ Қойшыманова. А Проверила Қожахметова .Ж.Ж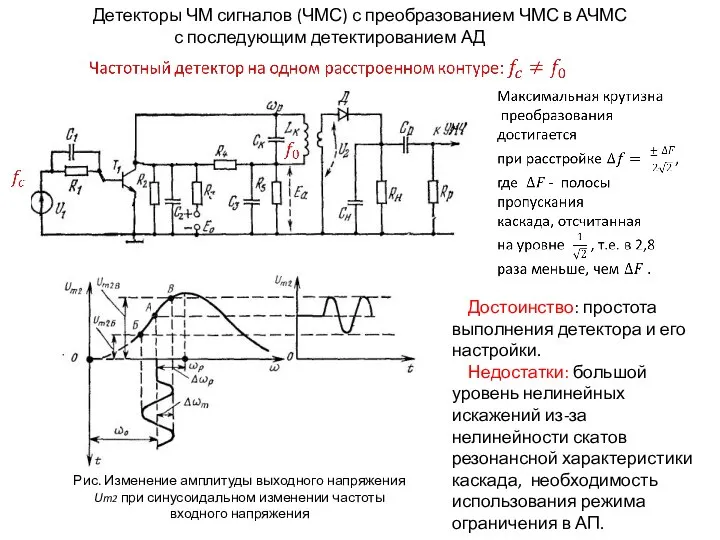 Детекторы ЧМ сигналов (ЧМС) с преобразованием ЧМС в АЧМС с последующим детектированием АД
Детекторы ЧМ сигналов (ЧМС) с преобразованием ЧМС в АЧМС с последующим детектированием АД Российское искусство XIX века
Российское искусство XIX века Компания «ИТ-Кострома» мы расширяем ваши возможности. Предложение партнерам фирмы 1С
Компания «ИТ-Кострома» мы расширяем ваши возможности. Предложение партнерам фирмы 1С Московский Кремль
Московский Кремль Планета Земля
Планета Земля Свобода слова: философские основания, политологическое содержание и правовые основы
Свобода слова: философские основания, политологическое содержание и правовые основы Презентация "С нами надежнее!" - скачать презентации по Экономике
Презентация "С нами надежнее!" - скачать презентации по Экономике