Слайд 6

Предикаты и примитивно-рекурсивные операторы
А – множество объектов хi (i=1,..,N),
утверждение P(x),
истинное для некоторых хi и ложное для остальных, называется одноместным предикатом на множестве А.
Декартово произведение множеств А1,…,АM:
А1хА2х…xАM: {(x1,x2,…,xm)|x1∈A1,…,xm∈AM}.
Для предиката вводится его характеристическая функция:
χP(x1,…,xn)= 1, если P(x1,…,xn) истинен,
0, в противном случае.
Условный переход или разветвление. Обозначим его B, который по функциям q1(x1,…,xn), q2(x1,…,xn) и предикату P(x1,…,xn) строит функцию f(x1,…,xn)=B(q1, q2, P):
f(x1,…,xn)= q1(x1,…,xn), если P(x1,…,xn) истинно.
q2(x1,…,xn), если P(x1,…,xn) ложно.
f(x1,…,xn)=g1(x1,…,xn) χp(x1,…,xn)+g2(x1,…,xn) (1- χp(x1,…,xn)).







 Митрофанов Владислав Владимирович. Обыкновенное чудо – люди России
Митрофанов Владислав Владимирович. Обыкновенное чудо – люди России Portes ouvertes adultes
Portes ouvertes adultes Лоббирование. Контрлоббирование
Лоббирование. Контрлоббирование Таджикистан
Таджикистан УПРАВЛЕНИЕ ПЕРСОНАЛОМ
УПРАВЛЕНИЕ ПЕРСОНАЛОМ Основы программирования
Основы программирования Чертежный шрифт. Сопряжение. Виды. Разрезы
Чертежный шрифт. Сопряжение. Виды. Разрезы Учитель математики: Агаджанян Л. В. Школа №324 Курортного района
Учитель математики: Агаджанян Л. В. Школа №324 Курортного района Понятие права и его признаки Баделько К. С. Тс06-1406
Понятие права и его признаки Баделько К. С. Тс06-1406  Графика_Python
Графика_Python Складирование конструкций
Складирование конструкций Товарищество передвижных художественных выставок
Товарищество передвижных художественных выставок Анализ рынка. Интернет-магазин по продаже стикеров
Анализ рынка. Интернет-магазин по продаже стикеров Музей Квітки Цісик
Музей Квітки Цісик Система компенсации давления
Система компенсации давления Расчет силовых нагрузок на вал и построение эпюр изгибающих моментов и крутящего момента
Расчет силовых нагрузок на вал и построение эпюр изгибающих моментов и крутящего момента Архитектура и искусство Великобритании XVIІІ в
Архитектура и искусство Великобритании XVIІІ в Пешеходная улица в Сыктывкаре
Пешеходная улица в Сыктывкаре Рекомендации по выбору посадок
Рекомендации по выбору посадок Денсаулық сақтаудағы менеджмент
Денсаулық сақтаудағы менеджмент Игра волейбол
Игра волейбол Что это?
Что это? ПРОФЕССИОНАЛЬНАЯ КОМПЕТЕНТНОСТЬ МЕНЕДЖЕРА ОБРАЗОВАНИЯ
ПРОФЕССИОНАЛЬНАЯ КОМПЕТЕНТНОСТЬ МЕНЕДЖЕРА ОБРАЗОВАНИЯ моделирование схем аналоговых электронных устройств. Генераторы синусоидальных колебаний
моделирование схем аналоговых электронных устройств. Генераторы синусоидальных колебаний Презентация на тему "Федеральный государственный образовательный стандарт общего образования в контексте государственной пол
Презентация на тему "Федеральный государственный образовательный стандарт общего образования в контексте государственной пол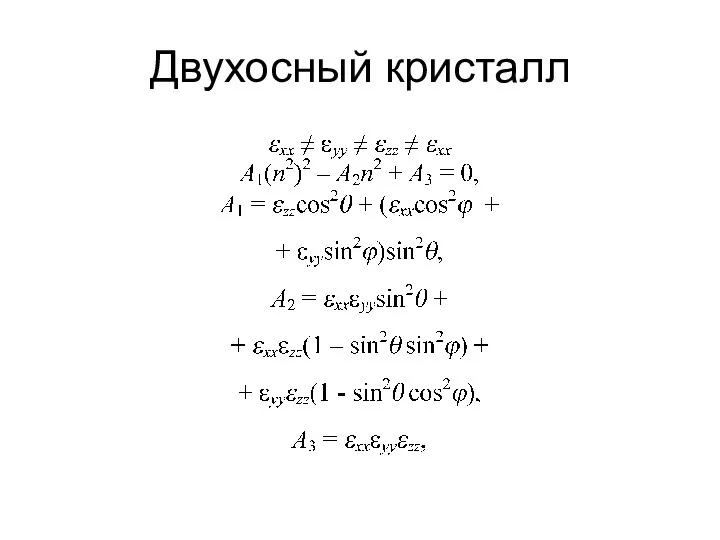 Двухосный кристалл
Двухосный кристалл Профилактика травматизма на уроках физической культуры и в спорте
Профилактика травматизма на уроках физической культуры и в спорте Взаимодействие между процессами
Взаимодействие между процессами