Содержание
- 2. Неформальное и формальное определение МТ. Конфигурации. УУ Конечное множество состояний УУ: Q={q1,…, qn}. Алфавит: Σ= {a1,…,am}.
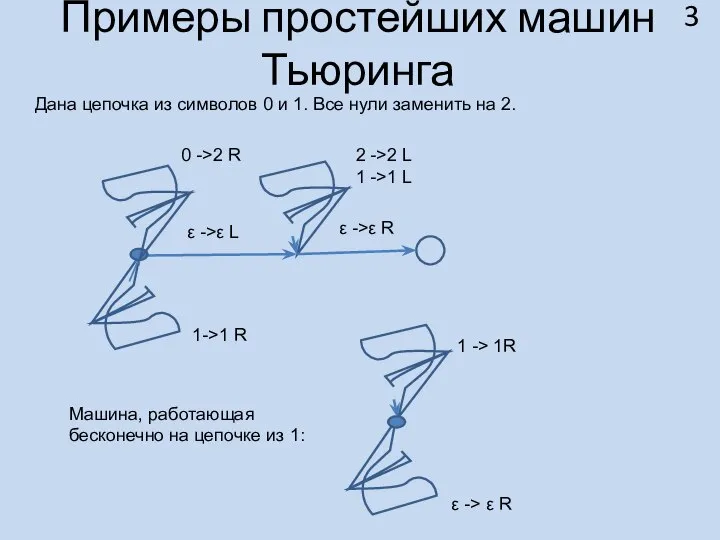
- 3. Примеры простейших машин Тьюринга Дана цепочка из символов 0 и 1. Все нули заменить на 2.
- 4. Переработка цепочек. Вычислимость по Тьюрингу. Если α1 q0 α2 =>β1 qz β2, то будем говорить, что
- 5. Вычислимость композиции Композиция g (x) = f2 (f1(x)) T1 и T2 - машины, вычисляющие f1 и
- 6. Вычислимость на полуленте и с восстановлением df Говорят, что Т вычисляет предикат P(α), если T(α) =
- 7. Вычислимость разветвления Теорема. Если функции g1(α), g2(α) и предикат Р(α) вычислимы по Тьюрингу, то разветвление g1(α)
- 9. Скачать презентацию





 Православное учение о человеке
Православное учение о человеке 시조에 나타난 한국인의 멋
시조에 나타난 한국인의 멋 Оценка нервно-психического развития у детей
Оценка нервно-психического развития у детей Политическая элита, лидеры, партии
Политическая элита, лидеры, партии Спорт-кейс
Спорт-кейс ИСОД - единая система информационно-аналитического обеспечения деятельности МВД России
ИСОД - единая система информационно-аналитического обеспечения деятельности МВД России История развития бухгатерского учета зарубежом
История развития бухгатерского учета зарубежом  Евфросиния Полоцкая и Кирилл Туровский
Евфросиния Полоцкая и Кирилл Туровский Динамические и статистические закономерности в природе
Динамические и статистические закономерности в природе Ключи к здоровью позвоночника и суставов. Тренинг
Ключи к здоровью позвоночника и суставов. Тренинг Маркетинг и маркетинговые исследования
Маркетинг и маркетинговые исследования Автоматизированное тестирование
Автоматизированное тестирование РОССИЙСКО-ЯПОНСКАЯ ОРГАНИЗАЦИЯ ПО СОДЕЙСТВИЮ ТОРГОВЛЕ И ИНВЕСТИЦИЯМ
РОССИЙСКО-ЯПОНСКАЯ ОРГАНИЗАЦИЯ ПО СОДЕЙСТВИЮ ТОРГОВЛЕ И ИНВЕСТИЦИЯМ  Особенности любовной лирики Ф.И Тютчева, ее напряженность, развитие
Особенности любовной лирики Ф.И Тютчева, ее напряженность, развитие Смирнова Т.А. учитель технологии МОУ СОШ № 3 г. Киржач
Смирнова Т.А. учитель технологии МОУ СОШ № 3 г. Киржач Основные направления авангарда Выполнила: Хочева Анна Группа Т-092
Основные направления авангарда Выполнила: Хочева Анна Группа Т-092 Структура как пользовательский тип и совокупность данных
Структура как пользовательский тип и совокупность данных Русская ярмарка
Русская ярмарка УРОК 1.УРОК 1.1.Значение слова «история». 2.Исторические источники. 3.Виды исторических источников. 4.Работа с историческими источника
УРОК 1.УРОК 1.1.Значение слова «история». 2.Исторические источники. 3.Виды исторических источников. 4.Работа с историческими источника Разминка по философии На тему: «Философское учение о человеке» Мб 02/1302 Тархов Сергей
Разминка по философии На тему: «Философское учение о человеке» Мб 02/1302 Тархов Сергей Принятые основные символы и обозначения
Принятые основные символы и обозначения Мотострелковый взвод в различных видах боя
Мотострелковый взвод в различных видах боя Теледидар
Теледидар Реконструкция подстанции 110/10 кВ, г. Россошь
Реконструкция подстанции 110/10 кВ, г. Россошь Трудовой договор
Трудовой договор Специальные диоды
Специальные диоды Спортивная командная игра баскетбол
Спортивная командная игра баскетбол Избирательные системы
Избирательные системы