Содержание
- 2. Там же было установлено, что устойчивость ЛДФ определяется условием, накладываемым на его импульсную характеристику. Была доказана
- 3. Теорема 2. Для того чтобы ЛДФ был устойчив, необходимо и достаточно, чтобы все полюсы zn передаточной
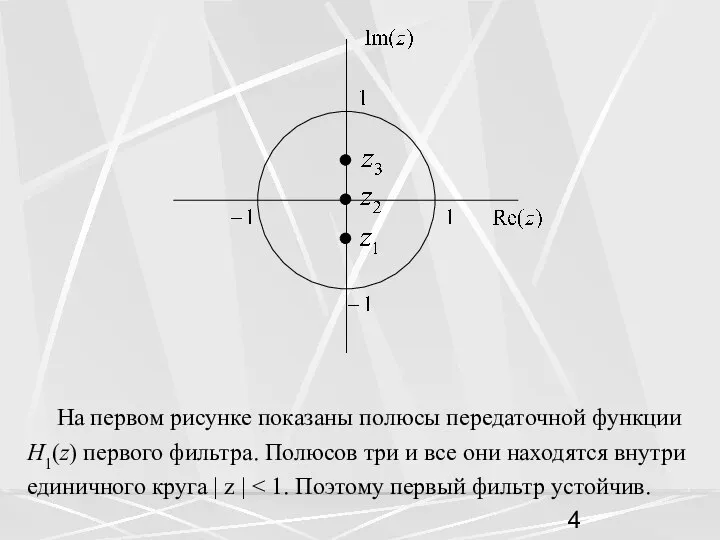
- 4. На первом рисунке показаны полюсы передаточной функции H1(z) первого фильтра. Полюсов три и все они находятся
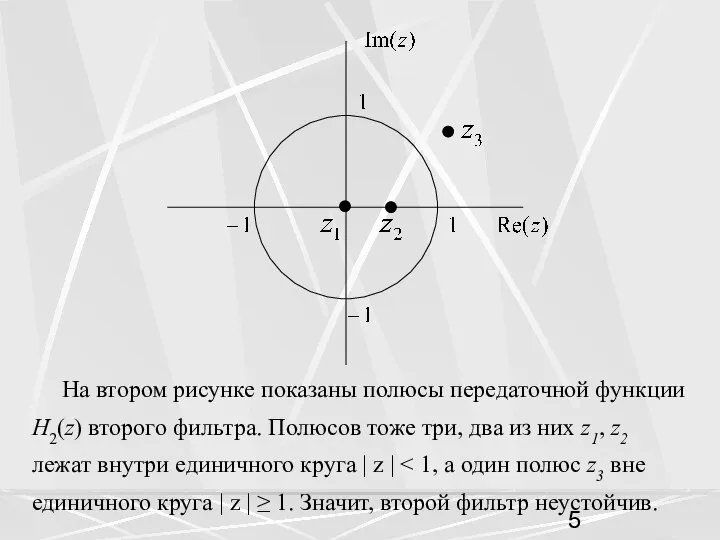
- 5. На втором рисунке показаны полюсы передаточной функции H2(z) второго фильтра. Полюсов тоже три, два из них
- 6. Пример 1. На прошлой лекции мы рассматривали рекурсивный фильтр, который описывался следующим разностным уравнением. (2) Надо
- 7. Единственная особая точка передаточной функции – это полюс первого порядка . Согласно теореме 2, фильтр будет
- 8. Частотная характеристика ЛДФ Определение. Частотная характеристика линейного дискретного фильтра – это комплексная функция K(ω) действительного переменного
- 9. Вспомним, что передаточная функция H(z) является Z - образом импульсной характеристики h(n) фильтра. Поэтому передаточная функция
- 10. Поэтому частотную характеристику можно представить в виде ряда. (8) Если частотную характеристику фильтра рассматривать, как функцию
- 11. Вспомним, как определяется спектр дискретного сигнала. Для аналогового сигнала s(t) выбирается шаг дискретизации Δt , и
- 12. Вспомним, что условие физической реализуемости ЛДФ накладывает на импульсную характеристику условие. (13) Используя это условие, нижний
- 13. Мы видим, что формула (14) для частотной характеристики ЛДФ, и формула (11) для спектра дискретного сигнала
- 14. Так, например, частотная характеристика является периодической функцией частоты с периодом 2F . Кроме того, для вычисления
- 15. КИХ и БИХ фильтры Определение. Конечной импульсной характеристикой ЛДФ будем называть импульсную характеристику, имеющую конечное число
- 16. Бесконечной импульсной характеристикой ЛДФ будем называть импульсную характеристику, имеющую бесчисленное число элементов отличных от нуля. Другими
- 19. Рекурсивные и нерекурсивные фильтры и их связь с КИХ и БИХ фильтрами Напомним, что основное разностное
- 20. В зависимости от того, равны нулю все или не все коэффициенты an , фильтры разделяют на
- 21. Найдем импульсную характеристику h(n) нерекурсивного фильтра. Вспомним, что импульсную характеристику называют так же реакцией системы на
- 22. Таким образом, импульсная характеристика нерекурсивного фильтра находится очень просто, она равна коэффициентам bk основного разностного уравнения
- 23. Исследуем нерекурсивные фильтры на устойчивость. Для этого переходную функцию нерекурсивного фильтра (20) перепишем в следующем виде.
- 24. Для анализа устойчивости фильтра, важно, что эта особая точка лежит в комплексной плоскости в центре единичного
- 25. Найти импульсную характеристику фильтра h(n), переходную функцию фильтра H(z) и частотную характеристику фильтра K(ω). По формуле
- 26. Далее делая в формуле (27) для переходной функции подстановку получаем частотную характеристику. (28) Если хотя бы
- 27. Пример 3. Рекурсивный фильтр описывается следующим разностным уравнением. (29) Найти импульсную характеристику фильтра h(n), переходную функцию
- 29. Этот фильтр был нами разобран на прошлой лекции. Поэтому воспользуемся полученными результатами. Используя коэффициенты (30), по
- 30. Далее делая в формуле (32) для переходной функции подстановку (33) получаем частотную характеристику. (32)
- 31. Затем, используя явный вид переходной функции (32) , с помощью теоремы о вычетах находим импульсную характеристику.
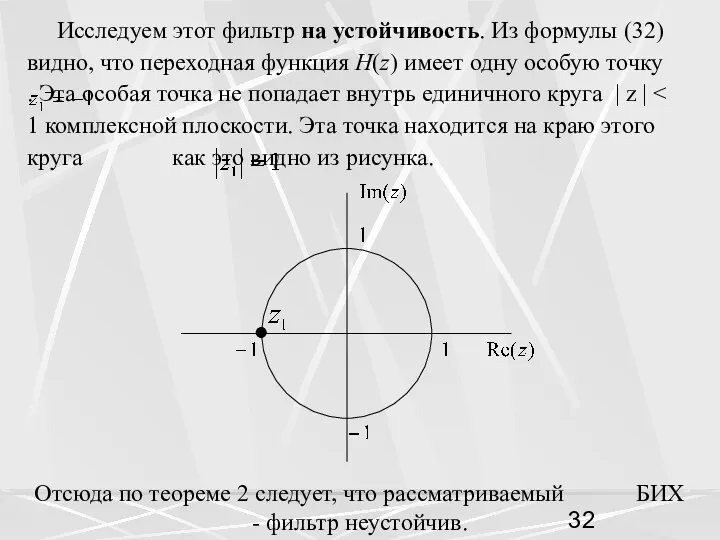
- 32. Исследуем этот фильтр на устойчивость. Из формулы (32) видно, что переходная функция H(z) имеет одну особую
- 33. Пример 4. На рисунке показана структурная схема рекурсивного фильтра.
- 34. Написать основное разностное уравнение этого фильтра. Найти импульсную характеристику фильтра h(n), переходную функцию фильтра H(z) и
- 35. По общей формуле (31) для переходной функции, подставляя туда коэффициенты (35) находим переходную функцию рассматриваемого фильтра.
- 36. Выпишем несколько значений функции f(z) для некоторых n . (39) Из соотношений (39) видно, что особая
- 37. Если n = 0 , то функция f(z) имеет полюс первого порядка в точке . Теперь
- 38. Как мы показали выше, все КИХ – фильтры являются устойчивыми фильтрами. Значит, рассматриваемый рекурсивный фильтр является
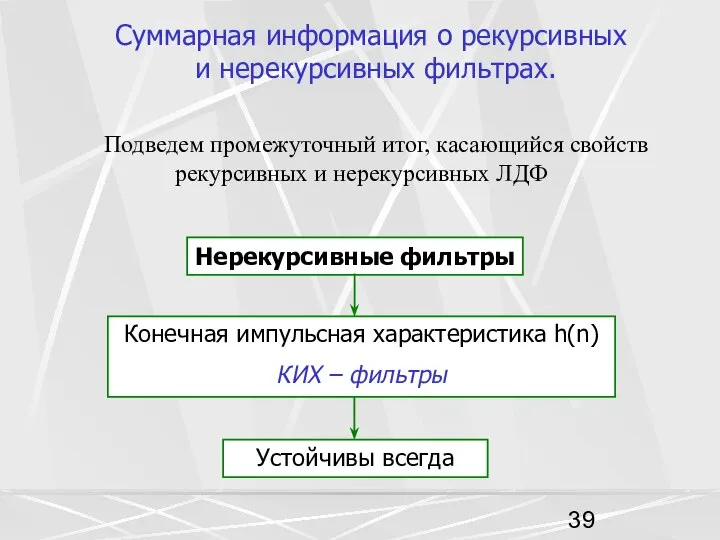
- 39. Суммарная информация о рекурсивных и нерекурсивных фильтрах. Подведем промежуточный итог, касающийся свойств рекурсивных и нерекурсивных ЛДФ
- 41. Аналоговые фильтры Как мы говорили ранее, в основе многих методов проектирования дискретных фильтров лежат методы проектирования
- 42. (43) Здесь x(t) - входящий сигнал, а y(t) - выходящий сигнал. Комплексный коэффициент передачи фильтра является
- 43. Классификация фильтров по их АЧХ 1. Фильтры нижних частот (ФНЧ, английский термин – low-pass filter), пропускающие
- 44. 2. Фильтры верхних частот (ФВЧ, английский термин – high-pass filter), пропускающие частоты, больше некоторой частоты среза
- 45. 3. Полосовые фильтры (ПФ, английский термин – band-pass filter), пропускающие частоты в некотором диапазоне . Такие
- 47. 3. Режекторные фильтры (РФ, английский термин – band-stop filter). Имеются другие названия таких фильтров – заграждающий
- 49. Передаточная функция аналогового фильтра Передаточная функция H(s) аналогового фильтра является изображением Лапласа импульсной характеристики h(t). (46)
- 50. Основным уравнением аналогового фильтра является следующее дифференциальное уравнение. (47) В этом дифференциальном уравнении ai , bi
- 51. Если эти коэффициенты заданы, то передаточная функция определятся следующей формулой. (48) Комплексный коэффициент передачи фильтра и
- 52. Поэтому АЧХ и ФЧХ аналогового фильтра легко найти, если мы знаем переходную функцию. Разложив числитель и
- 53. Фильтры Баттерворта Фильтры Баттерворта это фильтры нижних частот. Передаточная функция H(s) определяется n полюсами, которые задаются
- 54. Число n определяет порядок фильтра Баттерворта. На рисунке показано расположение полюсов для фильтра Баттерворта 5-го порядка
- 55. Передаточная функция H(s) для фильтра Баттерворта конструируется из полюсов следующим образом. (53) Здесь k0 - нормировочный
- 56. Теперь из формулы (54) можно найти АЧХ и ФЧХ фильтра Баттерворта n - го порядка. Простые,
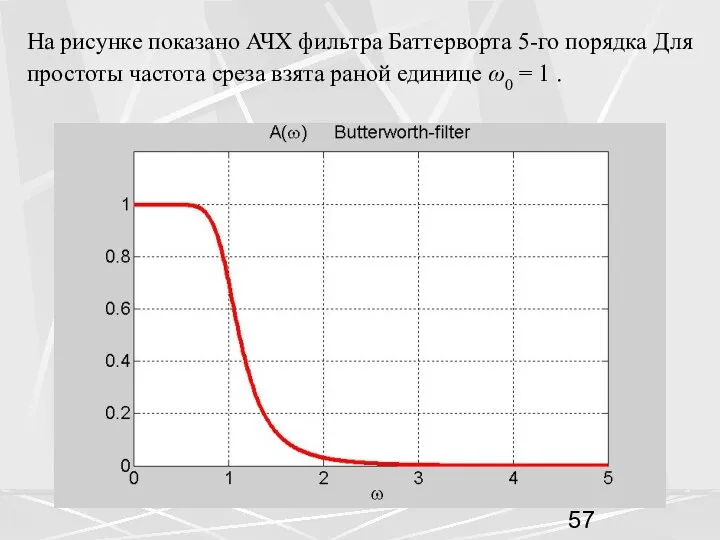
- 57. На рисунке показано АЧХ фильтра Баттерворта 5-го порядка Для простоты частота среза взята раной единице ω0
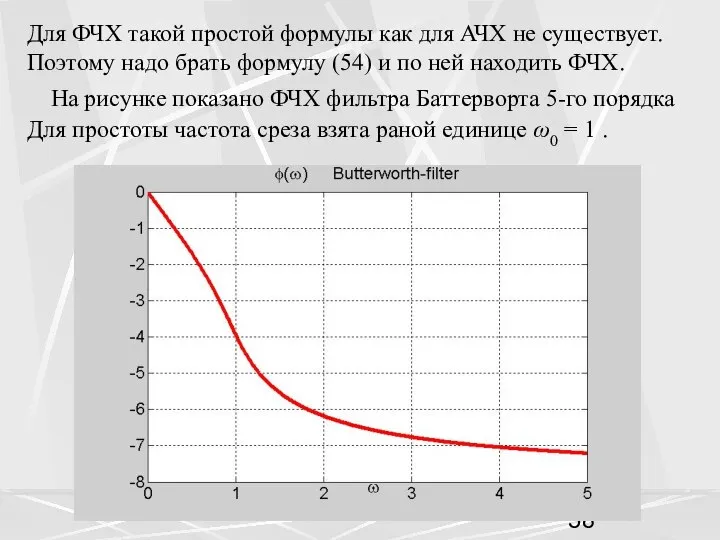
- 58. На рисунке показано ФЧХ фильтра Баттерворта 5-го порядка Для простоты частота среза взята раной единице ω0
- 59. Фильтр Чебышева первого рода Фильтр Чебышева первого рода является фильтром нижних частот. Передаточная функция этого фильтра
- 60. Здесь ω0 - частота среза, Tn (x)- полином Чебышева n - го порядка. Параметр ε определяет
- 61. На следующих двух рисунках показаны АЧХ ФЧХ для фильтра Чебышева первого рода 5-го порядка. Уровень пульсаций
- 64. Скачать презентацию























































 Роль интеграции предметов гуманитарного цикла в повышении качества образования.
Роль интеграции предметов гуманитарного цикла в повышении качества образования. Проект системы освещения жилого дома
Проект системы освещения жилого дома Презентация "Сравнение банков" - скачать презентации по Экономике
Презентация "Сравнение банков" - скачать презентации по Экономике Развитие устной речи у учащихся на основе аутентичного художественного фильма. Учитель:Ермакова Н.В.
Развитие устной речи у учащихся на основе аутентичного художественного фильма. Учитель:Ермакова Н.В. Физическая активность и здоровье
Физическая активность и здоровье Презентация "Основные подходы к построению математических моделей систем" - скачать презентации по Экономике
Презентация "Основные подходы к построению математических моделей систем" - скачать презентации по Экономике Биологическое окисление
Биологическое окисление  Основы программирования. Цикл for
Основы программирования. Цикл for Организация многофункционального пространства. Московский район
Организация многофункционального пространства. Московский район Гаагские конвенции 1899 и 1907 годов: эволюция международного гуманитарного права на случай войны. (анализ документов)
Гаагские конвенции 1899 и 1907 годов: эволюция международного гуманитарного права на случай войны. (анализ документов) Строительная компания TajiCK
Строительная компания TajiCK Все умеют рисовать! Рисуем с помощью ладошки.
Все умеют рисовать! Рисуем с помощью ладошки.  Рулевое управление
Рулевое управление Полупроводниковые диоды
Полупроводниковые диоды Как ухаживать за собаками и кошками? Как ухаживать за собаками и кошками? Учитель начальных классов МОУСОШ №4 города Тулы Климов
Как ухаживать за собаками и кошками? Как ухаживать за собаками и кошками? Учитель начальных классов МОУСОШ №4 города Тулы Климов Культура в меняющемся мире Изобразительное искусство Архитектура
Культура в меняющемся мире Изобразительное искусство Архитектура Презентация "Искусство. Виды искусства" - скачать презентации по МХК
Презентация "Искусство. Виды искусства" - скачать презентации по МХК Тормозная рычажная передача электровоза ВЛ 80
Тормозная рычажная передача электровоза ВЛ 80 Интернет-технологии
Интернет-технологии Информационные технологии в менеджменте. (Лекция 1)
Информационные технологии в менеджменте. (Лекция 1) Глухие и звонкие парные согласные в корне слова Белова Оксана Юрьевна, учитель начальных классов, МОУ СОШ №6 г. Реутова Московско
Глухие и звонкие парные согласные в корне слова Белова Оксана Юрьевна, учитель начальных классов, МОУ СОШ №6 г. Реутова Московско Теорема Пойнтинга
Теорема Пойнтинга Лекция 9. Ислам
Лекция 9. Ислам Комплексный эколого-краеведческий проект «Создание пеше-водного маршрута «Вниз по речке Василевке в сказку озера Сапшо»
Комплексный эколого-краеведческий проект «Создание пеше-водного маршрута «Вниз по речке Василевке в сказку озера Сапшо» Виды кабелей для компьютеров. Разъёмы
Виды кабелей для компьютеров. Разъёмы Błogosławiony Edmund Bojanowski
Błogosławiony Edmund Bojanowski Презентация Safe Case
Презентация Safe Case Репродукции художника Ряннеля Т.В
Репродукции художника Ряннеля Т.В