Содержание
- 2. АЧХ и ФЧХ фильтра находят как модуль и фазу комплексного коэффициента передачи. (2) Свойства фильтра определяются
- 3. Передаточная функция, выраженная через коэффициенты ai , bi , имеет вид. (4) Передаточная функция, выраженная через
- 4. Фильтр Чебышева первого рода Фильтр Чебышева первого рода является фильтром нижних частот. Передаточная функция этого фильтра
- 6. Фильтр Чебышева первого рода имеет простые полюсы в точках (6) Здесь штрихи обозначают действительную и мнимую
- 7. (8) Параметр ε определяет величину пульсаций АЧХ в полосе пропускания. Число n определяет порядок фильтра. Легко
- 8. Используя связь (1) между передаточной функцией H(s) и комплексным коэффициентом передачи K(ω), находим комплексный коэффициент передачи.
- 9. (11) Здесь ω0 - частота среза, Tn (x) - полином Чебышева n - го порядка. Полином
- 10. Для полиномов Чебышева существует также рекуррентная формула. (13) С помощью рекуррентной формулы (13) найдем некоторые из
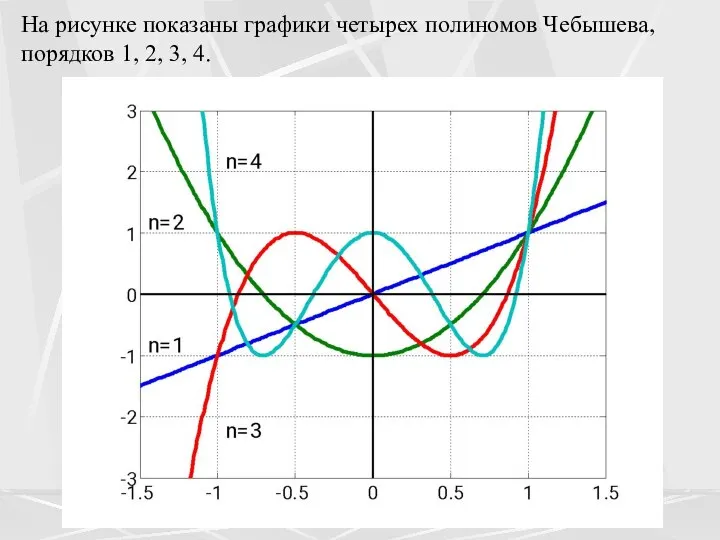
- 11. На рисунке показаны графики четырех полиномов Чебышева, порядков 1, 2, 3, 4.
- 12. Из формул (12) и из графиков, можно увидеть интересное свойство полиномов Чебышева. Полиномы Чебышева Tn (x)
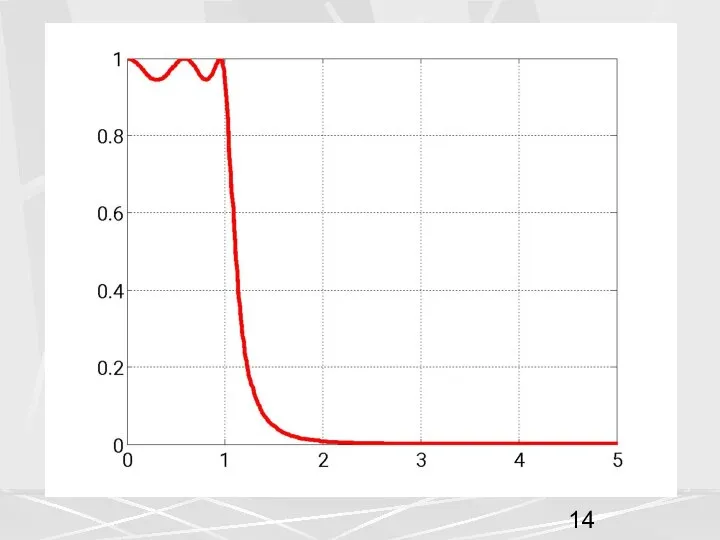
- 13. Благодаря этому свойству полиномов Чебышева, АЧХ фильтра Чебышева первого рода (11) в полосе пропускания колеблется между
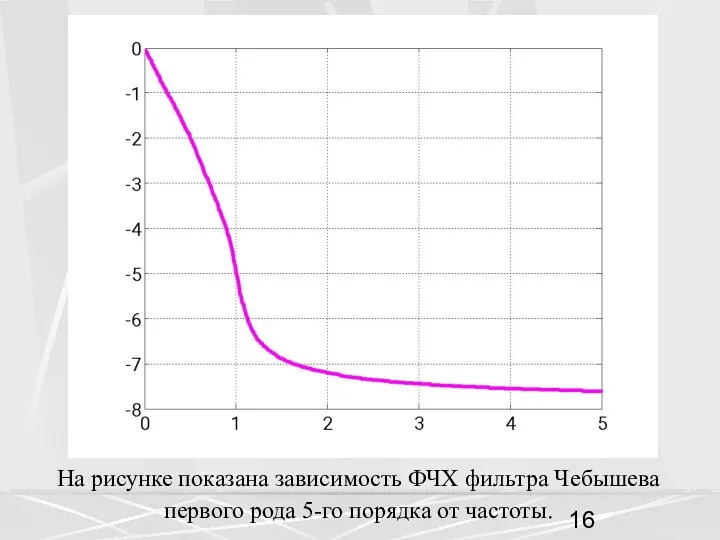
- 15. Для ФЧХ фильтра не существует, такой простой аналитической формулы, как для АЧХ фильтра. Поэтому находить ФЧХ
- 16. На рисунке показана зависимость ФЧХ фильтра Чебышева первого рода 5-го порядка от частоты.
- 17. Значение параметра ε связывают обычно с уровнем пульсаций Rp (в децибелах) по следующей формуле. (18) Графики
- 18. Три основных условия синтеза фильтров. Поставим вопрос, хорош ли фильтр Чебышева первого рода, как фильтр низких
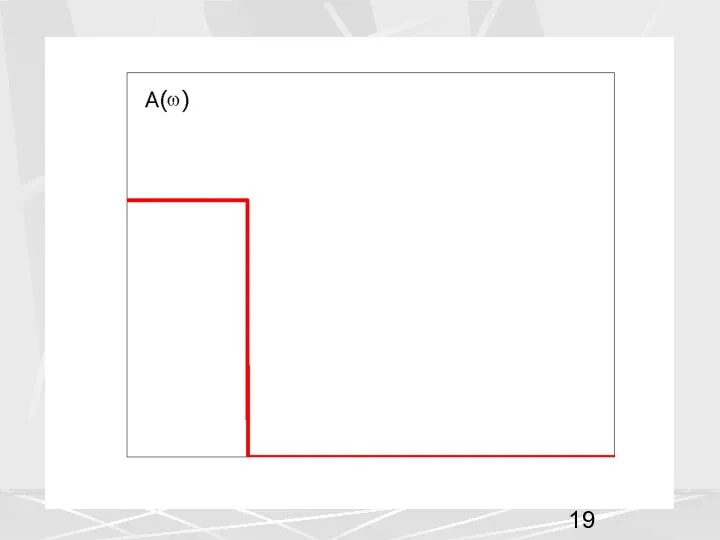
- 20. Сравнивая АЧХ идеального фильтра и АЧХ фильтра Чебышева, мы видим, что частотном спектре имеются три области,
- 21. 2) Во-вторых, это полоса задерживания ω > ω0 . У идеального фильтра в этой полосе АЧХ
- 22. 3) В-третьих, это полоса перехода от полосы пропускания к полосе задерживания. У идеального фильтра ширина этой
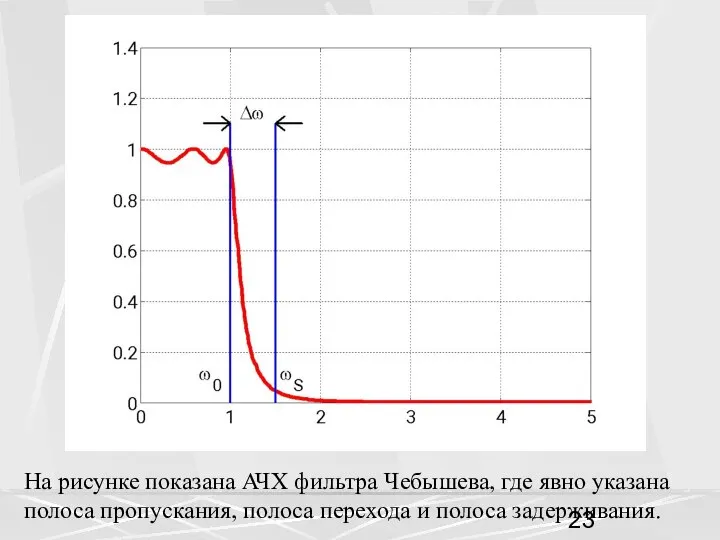
- 23. На рисунке показана АЧХ фильтра Чебышева, где явно указана полоса пропускания, полоса перехода и полоса задерживания.
- 24. Таким образом, при конструировании (при синтезе) реального фильтра приходится одновременно решать три задачи. 1. В полосе
- 25. 3. Полосу перехода АЧХ фильтра, необходимо сделать как можно меньше. (21) Как правило, три условия (19),
- 26. Теперь посмотрим, чем хорош фильтр Чебышева первого рода. Фильтр Чебышева первого рода n-го порядка является оптимальным
- 27. Фильтр Чебышева второго рода Фильтр Чебышева второго рода обеспечивает монотонное изменение АЧХ в полосе пропускания и
- 29. Передаточная функция фильтра Чебышева второго рода имеет и нули и полюсы. Она связана с передаточной функцией
- 30. Другими словами полюсы этих фильтров Чебышева являются обратными друг другу. По этой причине фильтр Чебышева второго
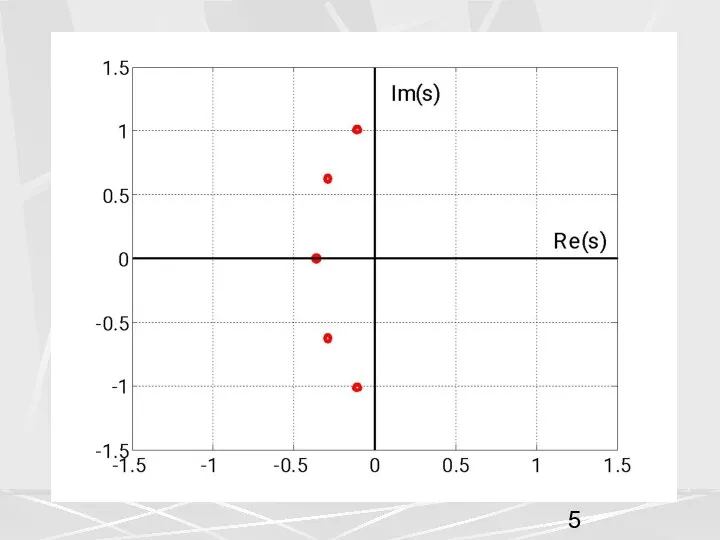
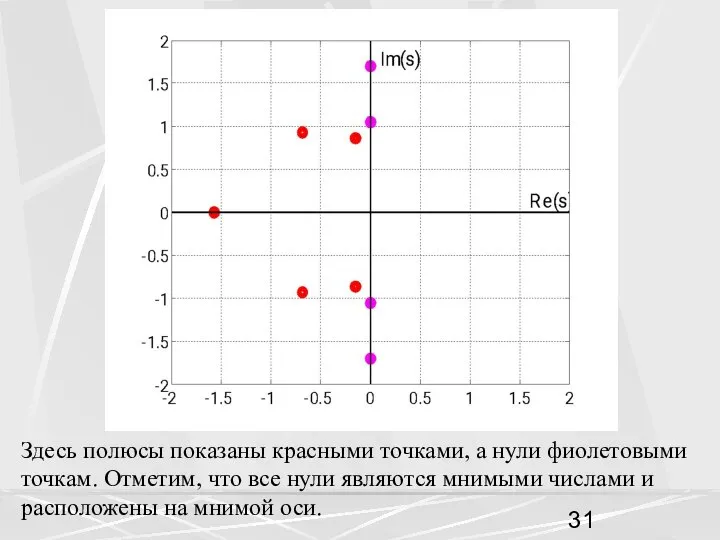
- 31. Здесь полюсы показаны красными точками, а нули фиолетовыми точкам. Отметим, что все нули являются мнимыми числами
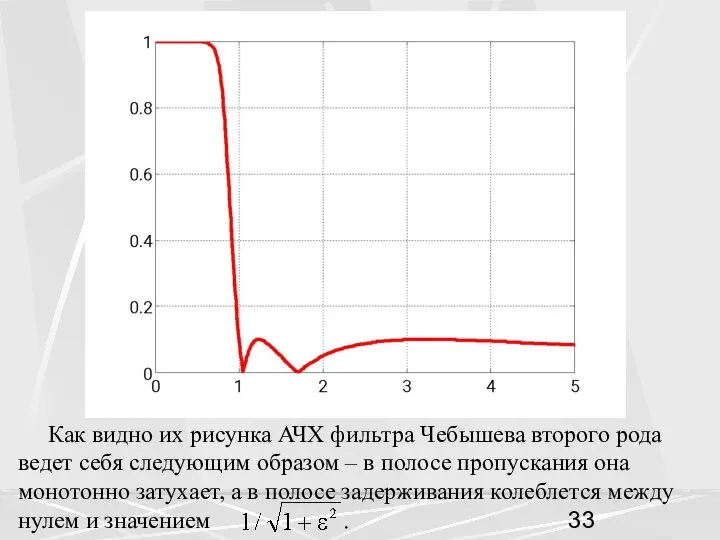
- 32. АЧХ фильтра Чебышева второго рода выражается простой аналитической формулой. (24) Здесь ε - параметр, определяющий величину
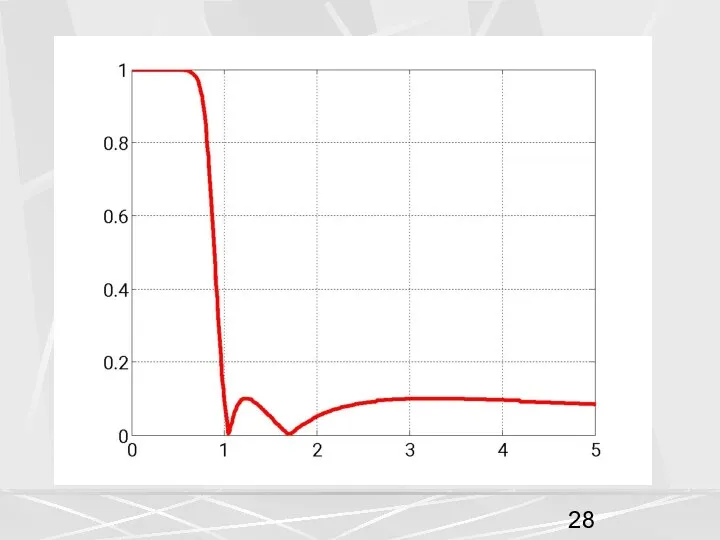
- 33. Как видно их рисунка АЧХ фильтра Чебышева второго рода ведет себя следующим образом – в полосе
- 34. (25) Значение параметра ε связывают обычно с уровнем пульсаций Rs в полосе задерживания (в децибелах) по
- 35. Это значит, что самое большое значение АЧХ в полосе задерживания равнялось 0.1 Это и видно на
- 37. Скачать презентацию

























 Технология обработки заготовок деталей машин резанием
Технология обработки заготовок деталей машин резанием Теоретико-методологические направления изучения здоровья
Теоретико-методологические направления изучения здоровья Мозаика в наследии Ломоносова
Мозаика в наследии Ломоносова Конкурентные стратегии компании
Конкурентные стратегии компании  Брачный договор во Франции
Брачный договор во Франции Радикальна партія Олега Ляшка
Радикальна партія Олега Ляшка Школьная форма - это здорово! Перминова Екатерина Школа 619 4г класс
Школьная форма - это здорово! Перминова Екатерина Школа 619 4г класс ЯЗЫК ПРОГРАММИРОВАНИЯ СИ
ЯЗЫК ПРОГРАММИРОВАНИЯ СИ ОРГАНЫ ПО СЕРТИФИКАЦИИ НАЦИОНАЛЬНЫЕ ТРЕБОВАНИЯ
ОРГАНЫ ПО СЕРТИФИКАЦИИ НАЦИОНАЛЬНЫЕ ТРЕБОВАНИЯ Гостиница «Днепр» - Hotel "Dnipro"
Гостиница «Днепр» - Hotel "Dnipro" Корпускулярно-волновой дуализм
Корпускулярно-волновой дуализм  Здравствуй , праздник Новый Год
Здравствуй , праздник Новый Год Конференция учащихся «Шаг в будущее»
Конференция учащихся «Шаг в будущее» Презентация на тему Рынок труда и безработица
Презентация на тему Рынок труда и безработица Презентация Западничество
Презентация Западничество Лекция 1. Образовательная политика в России. Основные направления модернизации образования. План 1. Роль государства и обще
Лекция 1. Образовательная политика в России. Основные направления модернизации образования. План 1. Роль государства и обще Методика развития гибкости у детей 8-9 лет, занимающихся греко-римской борьбой
Методика развития гибкости у детей 8-9 лет, занимающихся греко-римской борьбой Сокращение и нераспространение ядерного оружия. (Тема 8)
Сокращение и нераспространение ядерного оружия. (Тема 8) Современный театр Африки
Современный театр Африки Электропривод механизма
Электропривод механизма Последовательно-соединенные цепи. Реальная индуктивная катушка и конденсатор в цепи синусоидального тока. (Лекция 4)
Последовательно-соединенные цепи. Реальная индуктивная катушка и конденсатор в цепи синусоидального тока. (Лекция 4) Стадионы Чемпионата Мира по футболу 2018 года
Стадионы Чемпионата Мира по футболу 2018 года Бысровозводимые дома и их разновидности
Бысровозводимые дома и их разновидности Ислам мәдениеті
Ислам мәдениеті Викторина. Знаешь-ли ты этикет
Викторина. Знаешь-ли ты этикет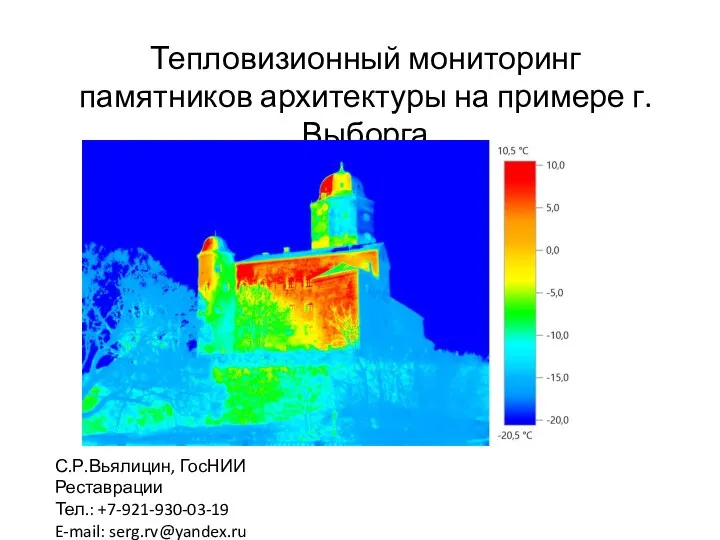 Тепловизионный мониторинг памятников архитектуры на примере г.Выборга
Тепловизионный мониторинг памятников архитектуры на примере г.Выборга Список литературы по ГОСТ
Список литературы по ГОСТ Презентация на тему "Первая помощь при обморожении" - скачать презентации по Медицине
Презентация на тему "Первая помощь при обморожении" - скачать презентации по Медицине