Содержание
- 2. Свойства среднего выборочного Пусть X – выборка объема n значений случайной величины, имеющей матожидание a, дисперсию
- 3. Свойства среднего выборочного 2.
- 4. Свойства среднего выборочного 3. 4.
- 5. Свойства начальных моментов
- 6. Свойства выборочной дисперсии
- 7. Распределение χ2 Распределением χ2 с k степенями свободы называется распределение случайной величины χ2(k), равной сумме квадратов
- 8. Плотность распределения χ2 при k=7
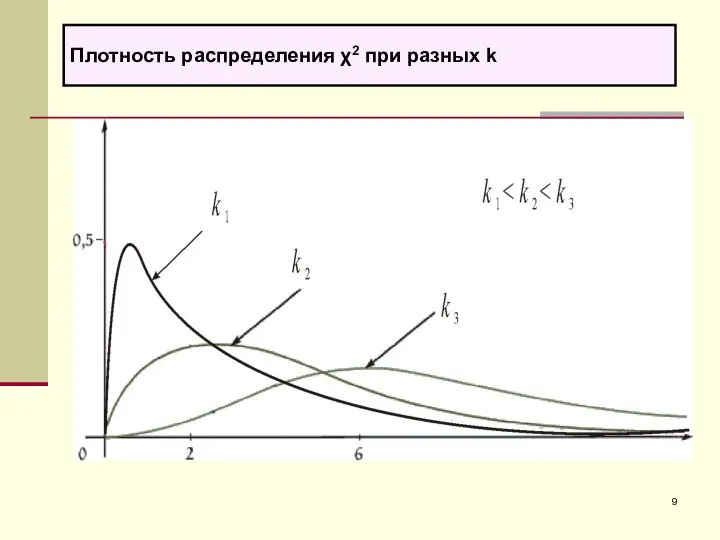
- 9. Плотность распределения χ2 при разных k
- 10. Плотность распределения χ2(k)
- 11. Замечание Если χ2(k1) и χ2(k2) независимые случайные величины, имеющие распределение χ2 с k1 и k2 степенями
- 12. Распределение Стьюдента Распределением Стьюдента с k степенями свободы называется распределение случайной величины Т(k), равной где U
- 13. Замечание Для приближенного выражения квантилей χ2p(k1) распределения χ2(k1) через квантили uр нормального распределения N(0,1) используют следующие
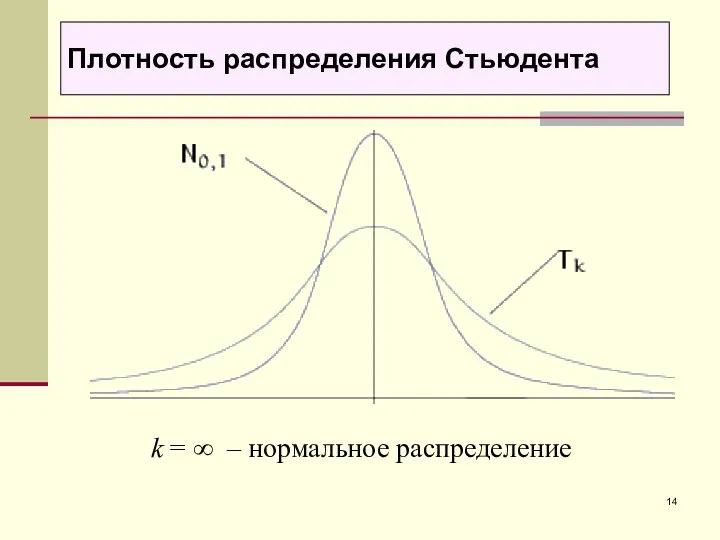
- 14. k = ∞ – нормальное распределение Плотность распределения Стьюдента
- 15. Распределение Стьюдента с k степенями свободы имеет плотность Плотность распределения Стьюдента
- 16. Плотность распределения Стьюдента симметрична относительно оси ординат, следовательно, для квантилей tp(k) имеет место соотношение tp(k)= –
- 17. Распределение Фишера Распределением Фишера с k1 и k2 степенями свободы называется распределение случайной величины F(k1, k2),
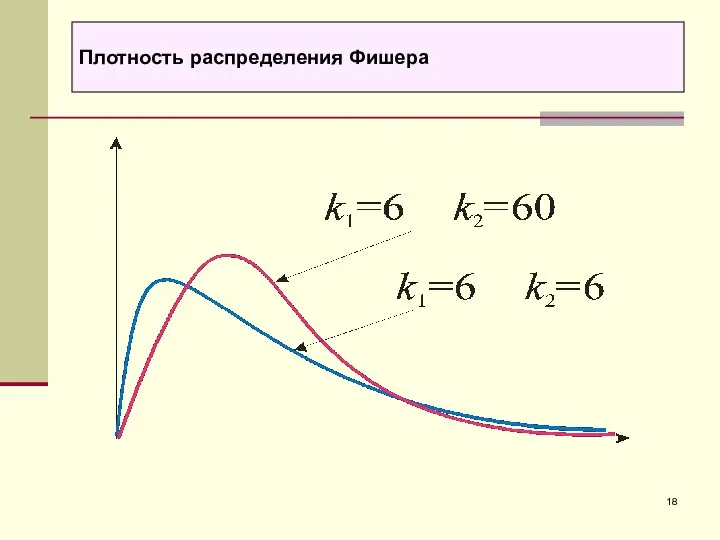
- 18. Плотность распределения Фишера
- 19. Распределение Фишера с k1 и k2 степенями свободы имеет плотность распределения Плотность распределения Фишера
- 20. Матожидание распределения Фишера
- 21. Квантили распределения Фишера порядка p и 1 –p связаны соотношением Замечание
- 22. Между случайными величинами, имеющими нормальное распределение, распределение χ2, распределение Стьюдента и распределением Фишера имеют место следующие
- 23. Теорема Фишера Пусть (X1, X2,..., Xn) – выборка из N(a, σ). Тогда:
- 25. Скачать презентацию



















 Машины переменного тока. Синхронные машины. Реакция якоря. (Лекция 5)
Машины переменного тока. Синхронные машины. Реакция якоря. (Лекция 5) Правапіс е, ё – я ў простых словах
Правапіс е, ё – я ў простых словах Конституциялық құқықтары мен міндеттері
Конституциялық құқықтары мен міндеттері Uniforme scolaire. "Pour" et "Contre"
Uniforme scolaire. "Pour" et "Contre" Христиан дінің негізгі ағымдары
Христиан дінің негізгі ағымдары Презентация на тему "Психолого-педагогическая диагностика классного руководителя Педагогика" - скачать презентации по Педаг
Презентация на тему "Психолого-педагогическая диагностика классного руководителя Педагогика" - скачать презентации по Педаг Значение и компоненты леса
Значение и компоненты леса  Введение в программирование (язык C, лекция 1)
Введение в программирование (язык C, лекция 1)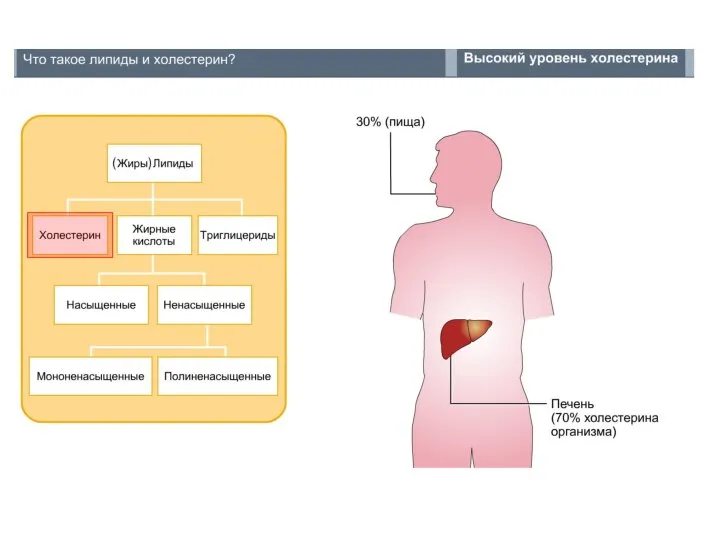 Холестерин
Холестерин скелет головы
скелет головы Русский язык 3 класс
Русский язык 3 класс Базисная терапия бронхиальной астмы
Базисная терапия бронхиальной астмы Питание и коррекция массы тела спортсменов
Питание и коррекция массы тела спортсменов Тема 4 Классические теории международной торговли
Тема 4 Классические теории международной торговли Спринклерлі және дренажды қондырғылар
Спринклерлі және дренажды қондырғылар Табличные распознаватели. Алгоритм Эрли. Алгоритм Кока—Янгера—Касами (Лекция 8)
Табличные распознаватели. Алгоритм Эрли. Алгоритм Кока—Янгера—Касами (Лекция 8) RAID - массивы
RAID - массивы Русский язык Влияние ударения на значение слов, которые одинаково пишутся. Составила: Морозова Татьяна Савельевна, учитель начал
Русский язык Влияние ударения на значение слов, которые одинаково пишутся. Составила: Морозова Татьяна Савельевна, учитель начал Доказательство корректности фрагментов программ с массивами
Доказательство корректности фрагментов программ с массивами Примеры стандартных сетей Ethernet
Примеры стандартных сетей Ethernet Бизнес-идея «FireDef». Огнезащитная штукатурка
Бизнес-идея «FireDef». Огнезащитная штукатурка СПИД
СПИД  Rachunek dla Mamy
Rachunek dla Mamy Культуры клеток
Культуры клеток  Ландшафтные закономерности структуры и динамики лесов
Ландшафтные закономерности структуры и динамики лесов Математическая игра. Олимпиада 2014
Математическая игра. Олимпиада 2014 Мережні архітектури. Планування, побудова і модернізація локальних мереж
Мережні архітектури. Планування, побудова і модернізація локальних мереж  Колье «Танец стерхов» с использованием техники стимпанк
Колье «Танец стерхов» с использованием техники стимпанк