Теория игр_10.05.2013.pptx

Содержание

Слайд 2

ТЕОРИЯ ИГР Аналогично может поступить и игрок A, неожиданно применив против

ТЕОРИЯ ИГР

Аналогично может поступить и игрок A, неожиданно применив против

игрока B стратегию, соответствующую максимальному элементу столбца .
Доказано [Вентцель Е.С. Исследование операций: Задачи, принципы, методология.
Учебное пособие- М.: Дрофа, 2004. ], что при многократно повторяемой игре без седловой точки игроку A, для обеспечения среднего выигрыша, большего, чем α , следует чередовать свои стратегии .
Игроку B для улучшения результата также целесообразно чередовать свои стратегии
Для многократно повторяемых игр без седловой точки вводится следующее определение.
• В играх, которые повторяются многократно, каждая из стратегий
называется чистой стратегией.
• Стратегия игрока A, обозначаемая
и состоящая в том, чтобы применять чистые стратегии , чередуя их по случайному закону с частотами , называется смешанной
стратегией. Частоты удовлетворяют соотношению
Слайд 3

ТЕОРИЯ ИГР • Чистые и смешанные стратегии игрока B определяются аналогично.

ТЕОРИЯ ИГР
• Чистые и смешанные стратегии игрока B определяются аналогично.


• Смешанные стратегии, избранные игроками, называются оптимальными, если одностороннее отклонение любым игроком от своей оптимальной стратегии может изменить средний выигрыш только в сторону, невыгодную для этого игрока.
• Совокупность, состоящая из оптимальной стратегии одного игрока
и оптимальной стратегии другого игрока, называется решением игры.
Средний выигрыш V при применении обоими игроками оптимальных стратегий называется ценой игры.
• Стратегии, входящие с ненулевыми частотами в оптимальную стратегию игрока, называются полезными.
Слайд 4

ТЕОРИЯ ИГР Нейманом была доказана основная теорема теории игр, утверждающая, что

ТЕОРИЯ ИГР

Нейманом была доказана основная теорема теории игр, утверждающая, что

каждая игра имеет, по крайней мере, одно решение, возможно, в области смешанных стратегий.
Поскольку чистые стратегии являются частными случаями смешанных стратегий, то из основной теоремы теории игр можно получить
Следствие1. Любая игра имеет цену.
Следствие2. Цена игры удовлетворяет неравенству
Следствие3. Средний выигрыш остается равным цене игры, если один
из игроков придерживается своей оптимальной стратегии, а другой игрок применяет свои полезные стратегии с любыми частотами.
Слайд 5

ТЕОРИЯ ИГР Аналитический метод решения игры типа 2 x 2 Рассмотрим

ТЕОРИЯ ИГР

Аналитический метод решения игры типа 2 x 2
Рассмотрим

игру без седловой точки типа 2 x 2 с платежной матрицей
и найдем оптимальную стратегию
игрока A.
Согласно следствию 3 из основной теоремы теории игр эта стратегия обеспечивает игроку A выигрыш, равный цене игры V, даже если игрок B не выходит за пределы своих полезных стратегий.
В данной игре обе чистые стратегии игрока B являются полезными, поскольку в противном случае игра имела бы решение в области чистых стратегий, т.е. была бы игрой с седловой точкой.
Слайд 6

ТЕОРИЯ ИГР Отсюда вытекает, что неизвестные удовлетворяют следующей системе из трех

ТЕОРИЯ ИГР

Отсюда вытекает, что неизвестные удовлетворяют следующей
системе из трех линейных

уравнений
решение которой имеет вид
Аналогичным образом можно найти оптимальную стратегию
игрока B. В этом случае неизвестные удовлетворяют системе урав-нений
Слайд 7

ТЕОРИЯ ИГР решение которой имеет вид Теперь наша задача применить полученные

ТЕОРИЯ ИГР
решение которой имеет вид
Теперь наша задача применить полученные формулы

к игровым задачам, возникающим с проектированием программного обеспечения.
Слайд 8

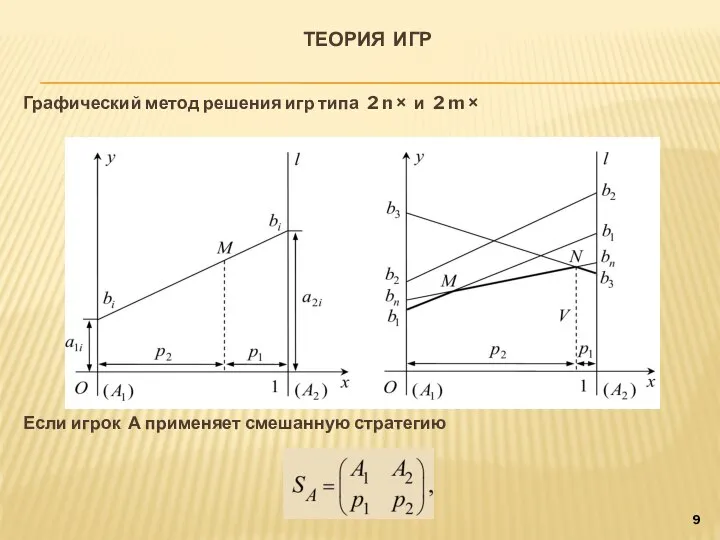
ТЕОРИЯ ИГР Графический метод решения игр типа 2 n × и

ТЕОРИЯ ИГР

Графический метод решения игр типа 2 n × и

2 m ×
Рассмотрим игру типа 2 n × с платежной матрицей
и проведем через точку (1; 0) координатной плоскости Oxy прямую l, перпендикулярную оси абсцисс.
После этого для каждой из стратегий проведем прямую
соединяющую точку на оси Оу с точкой на прямой l. Ось Оу отвечает за стратегию , а прямая l − за стратегию
Слайд 9

ТЕОРИЯ ИГР Графический метод решения игр типа 2 n × и

ТЕОРИЯ ИГР

Графический метод решения игр типа 2 n × и

2 m ×
Если игрок А применяет смешанную стратегию
Слайд 10

ТЕОРИЯ ИГР то его выигрыш в случае, если противник применяет чистую

ТЕОРИЯ ИГР

то его выигрыш в случае, если противник применяет чистую

стратегию
равен
и этому выигрышу соответствует точка М на прямой с абсциссой
Ломаная , отмеченная на чертеже жирной линией, позволяет определить минимальный выигрыш игрока А при любом поведении игрока В.
Точка N, в которой эта ломаная достигает максимума, определяет решение
и цену игры.
Ордината точки N равна цене игры V, а ее абсцисса частоте применения стратегии в оптимальной смешанной стратегии игрока А.
Далее непосредственно по чертежу можно найти пару «полезных» стратегий
игрока В, пересекающихся в точке N (если в точке N пересекается более
двух стратегий, то выбираются любые две из них).
Пусть это будут стратегии
Слайд 11

ТЕОРИЯ ИГР Графический метод решения игр типа 2 n × и

ТЕОРИЯ ИГР

Графический метод решения игр типа 2 n × и

2 m ×
Выигрыш игрока А, если он придерживается оптимальной стратегии, не зависит от того, в каких пропорциях игрок В применяет эти стратегии, поэтому неизвестные определяются из системы уравнений
Частоты в оптимальной стратегии
игрока В определяются из соотношения
Слайд 12

ТЕОРИЯ ИГР Графический метод решения игр типа 2 n × и

ТЕОРИЯ ИГР

Графический метод решения игр типа 2 n × и

2 m ×
Пример . Пусть игра задана матрицей
Найти оптимальные стратегии игроков и определить цену игры.
Решение.
Воспользовавшись тем, что игрок B располагает двумя чистыми стратегия-ми, построим прямые , соответствующие выигрышам игрока А при чистых стратегиях и ломаную линию , огибающую график сверху.
Эта ломаная достигает минимума в точке , которая является
пересечением прямых
Следовательно, , и оптимальной стратегией игрока В является стратегия
Слайд 13

ТЕОРИЯ ИГР Графический метод решения игр типа 2 n × и

ТЕОРИЯ ИГР

Графический метод решения игр типа 2 n × и

2 m ×
Цена игры V = 7,2.
Полезными стратегиями игрока А являются стратегии .
Найдем их частоты
Слайд 14

ТЕОРИЯ ИГР Прямоугольные игры ( без седловых точек): смешанные стратегии Пример.

ТЕОРИЯ ИГР

Прямоугольные игры ( без седловых точек): смешанные стратегии
Пример. Рассмотрим

игру с платежной матрицей, показанной в таблице 1. Платежная матрица не имеет седловой точки, т. к. в этой игре ни один из участников игры не может выбрать один план в качестве своей оптимальной стратегии.
Следовательно, каждый игрок должен найти некоторую «смешан­ную стратегию» для максимизации своего выигрыша или минимизации своего проигрыша.
Таблица 1
Допустим, например, что А решает играть половину времени по плану Р, а половину по плану Q. Если В при этом будет все время играть по плану S, то ожидаемый выигрыш для А будет
а если В будет все время играть по плану Т, то ожидаемый выигрыш игрока А будет
Слайд 15

ТЕОРИЯ ИГР Прямоугольные игры ( без седловых точек): смешанные стратегии Допустим

ТЕОРИЯ ИГР

Прямоугольные игры ( без седловых точек): смешанные стратегии
Допустим далее,

что В также применяет смешанную стратегию и в половине случаев выбирает план S, а в половине Т, причем каждый выбор определяет случайно. В этом случае ожидаемый выигрыш игрока А будет
Подобным образом можем подсчитать, каков ожидаемый выигрыш А при других смешанных стратегиях. Например, если А играет в четверти случаев план Р, a Q — в трех четвертях, в то время как В играет одну треть раз S, а две трети Т, то ожидаемый выигрыш А будет
Возникает вопрос: какова оптимальная смешанная стратегия для игро­ков? Из приведенных примеров видим, что выигрыш А меняется от 1,5 долларов до 4 долларов. Хотим узнать, не может ли игрок А обес­печить себе некоторый минимум выигрыша и каков он?
Подобным образом, может ли В застраховаться от проигрыша больше некоторого максималь­ного?
На эти вопросы можно ответить положительно. Математическая теория игр дает доказательство того, что всегда существуют оптимальные стра­тегии и способы их нахождения.
Слайд 16

ТЕОРИЯ ИГР Прямоугольные игры ( без седловых точек): смешанные стратегии Рассмотрим

ТЕОРИЯ ИГР

Прямоугольные игры ( без седловых точек): смешанные стратегии
Рассмотрим теперь,

как могут быть найдены оптимальные стратегии этой игры и каковы ожидаемые значения выигрыша и проигрыша для игроков.
Пусть А играет Р с частотой х, a Q с частотой 1 — х. Тогда, если В будет играть все время S, выигрыш А будет
Если В будет все время играть Т, выигрыш А будет
Математически можно показать, что если А выберет х так, что
то для него это будет оптимальной стратегией. Итак,
В результате получаем
Слайд 17

ТЕОРИЯ ИГР Прямоугольные игры ( без седловых точек): смешанные стратегии Таким

ТЕОРИЯ ИГР

Прямоугольные игры ( без седловых точек): смешанные стратегии
Таким образом,

независимо от частот, с которыми В играет S или Т, А всегда выигрывает 3 доллара. (Если, например, В играет S с частотой и Т с частотой
то ожидаемый выигрыш для А будет
и так же при любом выборе частот для В.) Следовательно, выбором частот 1/3 и 2/3
А получает обеспеченный выигрыш в 3 доллара.
Тот же самый метод можно применить к игроку В. Обозначим частоту выбора плана S буквой y, тогда частота выбора Т будет 1 - y . Для оптимальной стратегии имеем:
Заметим, что для игры с нулевой суммой.
Полным решением данной игры будет: (1) А следует играть Р и Q соответственно с
частотами 1/3 и 2/3; (2) В следует играть S и T с частотами 2/5 и 3/5; (3) цена игры — 3 доллара.
Слайд 18

ТЕОРИЯ ИГР Основные теоремы для прямоугольных игр. Платежи для прямоуголь­ных игр

ТЕОРИЯ ИГР

Основные теоремы для прямоугольных игр.
Платежи для прямоуголь­ных игр всегда

могут быть заданы в виде матрицы
m x n где игрок А имеет m возможных планов, В имеет п возможных планов и платежная матрица есть матрица (см. табл. 2).
Таблица 2
Математически можно показать, что (1) каждой прямоугольной игре соответствует определенное значение цены g; это значение единственно; (2) существует оптимальная стратегия игрока А, т. е., существуют частоты такие, что
и если игрок А
играет, применяя план I с частотой х1, план II с частотой х2 …., план m c частотой Хm , то он может обеспечить себе средний выигрыш не менее g, где g — цена игры; (3) также и для игрока В существует оптимальная стра­тегия
такая, что, если он применяет планы I, II, . . . , п с частотами y1,y2,…yn он обеспечивает себе проигрыш не больше g
Слайд 19

ТЕОРИЯ ИГР Основные теоремы для прямоугольных игр Для прямоугольной игры, матрица

ТЕОРИЯ ИГР

Основные теоремы для прямоугольных игр
Для прямоугольной игры, матрица которой

имеет седловую точку ( i0 , j0), имеем следующее решение
Общее решение прямоугольных игр. Можно показать, что неизвестные и g могут быть найдены из следующих соотношений:
Соотношение (3) в действительности представляет собой п неравенств, по одному неравенству для каждого j. Соотношение (4) представляет собой n неравенств. Таким образом, имеем m+n+1 неизвестных с m+n+2 соотношениями (с дополнительными ограничениями так как отрицательные частоты не имеют смысла).
Слайд 20

ТЕОРИЯ ИГР Основные теоремы для прямоугольных игр Теоремы предыдущей части гарантируют

ТЕОРИЯ ИГР

Основные теоремы для прямоугольных игр
Теоремы предыдущей части гарантируют существование

решения, удовлетворяющего этим соотношениям.
Они гарантируют также единственность g. Однако для игра может иметь несколько или даже бесконечное множество решений.
Пример. Для игры, представленной в таблице 1, неизвестными будут
и g. Соотношения следующие
(5)
(6)
(7)
(8)
(9)
(10)
Такие задачи могут быть решены при помощи «обычной алгебры», графиче­ским способом, применением матричной алгебры или итеративным мето­дом.
Слайд 21

ТЕОРИЯ ИГР Алгебраические решения Алгебраический метод — способ прямого нахождения неизвестных

ТЕОРИЯ ИГР

Алгебраические решения
Алгебраический метод — способ прямого нахождения неизвестных

из соотношений (1), (2), (3) и (4).
Решение осно­вано на указанном ранее факте: каждая прямоугольная игра имеет цену, а именно цену g, которая существует и единственна.
Необходимо найти одну такую цену g, которая удовлетворяет нашим соотношениям.
Для этого строим процедуру поиска цены g, опираясь на то, что она единственна.
Пер­вый шаг — предположить, что соотношения (3) и (4) суть равенства.
В этом случае получается следующая система уравнений:
Слайд 22

ТЕОРИЯ ИГР Алгебраические решения У нас имеется пять неизвестных и шесть

ТЕОРИЯ ИГР

Алгебраические решения
У нас имеется пять неизвестных и шесть уравнений.


Поэтому решим только пять уравнений и проверим, удовлетворяет ли найденное решение шестому.
Проверим также, удовлетворяют ли найденные значения неиз­вестных соотношениям
Если неизвестные удовлетворяют всем этим условиям, то они составляют полное решение.
Слайд 23

ТЕОРИЯ ИГР Алгебраические решения Уравнения (11) и (12) приводят к равенствам

ТЕОРИЯ ИГР

Алгебраические решения
Уравнения (11) и (12) приводят к равенствам
Следовательно,

(13), (14) и (15) переходят в следующие уравнения:
Складывая уравнения (17) и (18), находим т.е. х1=1/3 так что из уравнений (17), (18) и (11) получаем:
Подставляя эти значения в уравнение (16), получаем откуда
Поскольку имеем полное решение, а именно:
- Предыдущая
Теория игр
Следующая -
Исследования в области искуственного интеллекта

Похожие презентации

с детства дружбой дорожить... - презентация для начальной школы
Наступает Время Выбора: умей представить себя ( 9 класс) Если человек не знает, к какой пристани он держит путь, для него ни один вет
ОЦЕНКА УРОВНЯ КАЧЕСТВА ПРОДУКЦИИ ОЦЕНКА УРОВНЯ КАЧЕСТВА ПРОДУКЦИИ
История геохимии.
Міжнародні організації
Вычитание натуральных чисел - презентация по Алгебре
Где логика? Культурное наследие России
Власть. Власть как институт. Формы власти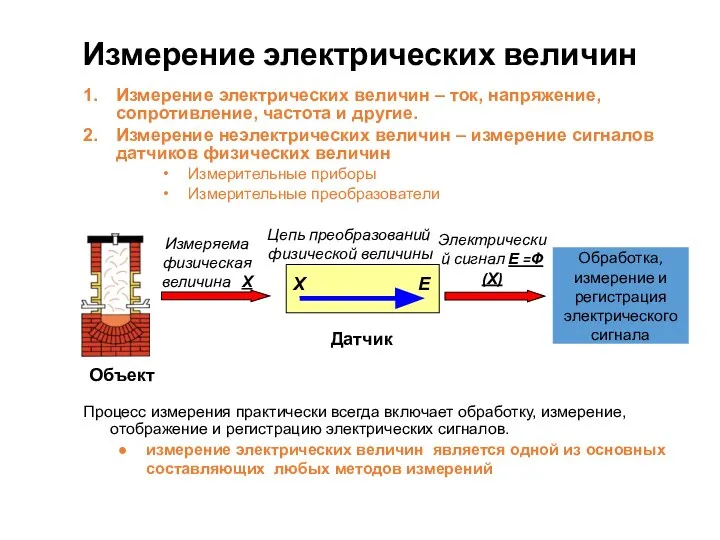
Измерение сопротивленений и RLC + цифр мосты
P9X79 Series Confidential
Фармацевтическая химия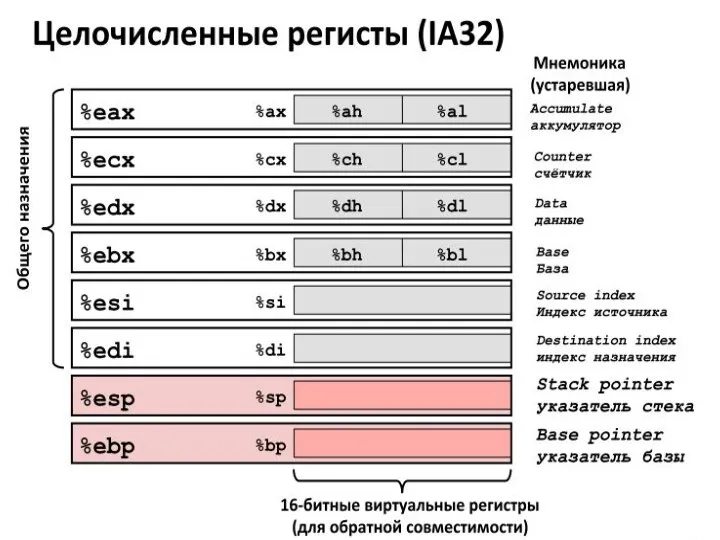
Сравнение языков ассемблера Intel and AT&T
Презентация на тему Моделирование как средство саморазвития учащихся в процессе учебной деятельности на уроках биологии
SOLID
Теория великих личностей
Условная трансляция Макрокоманды
Шаблонизация функций и классов
Влияние Интернета на русский язык
Речевое общение
DIXI CENTER. Разработка многофункциональных B2B2C систем
Академия здоровья. Катаракта, глаукома, близорукость и дальнозоркость
Основные физические свойства и характеристика нефти и нефтепродуктов
Тема урока; «Организационно-правовые формы предпринимательства» Цель урока: Познакомиться с основными признаками и орган
«Путешествие по страницам школьной жизни» Составитель: Иванова Марина Васильевна, учитель начальн
СЕБЕСТОИМОСТЬ ПРОДУКЦИИ
Изобретение Пина
Особенности присяжных заседателей Подготовила студентка 2-го курса Юридического факультета Турлаева лилиана
устный счет. решение задач 3 класс Долгополова нн - презентация для начальной школы
Вы можете прислать нам Вашу презентацию и мы опубликуем ее на сайте.
Обратная связь
Для правообладателей
Email: Нажмите что бы посмотреть