Сложное сопротивление
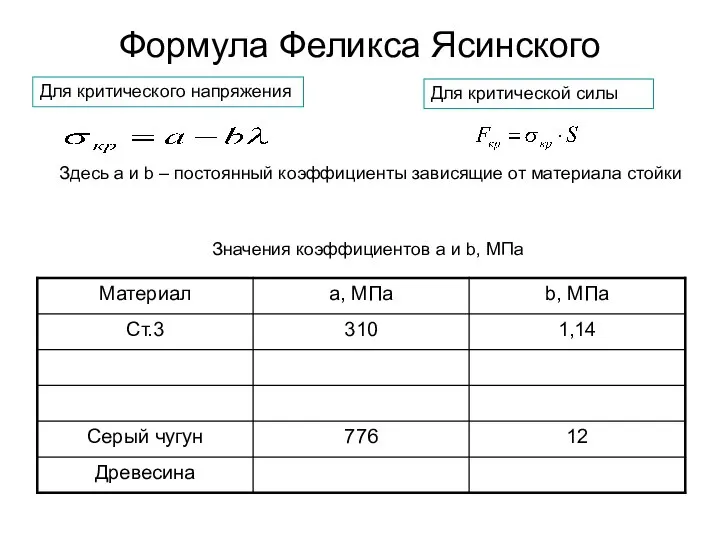
Сложный и косой изгиб
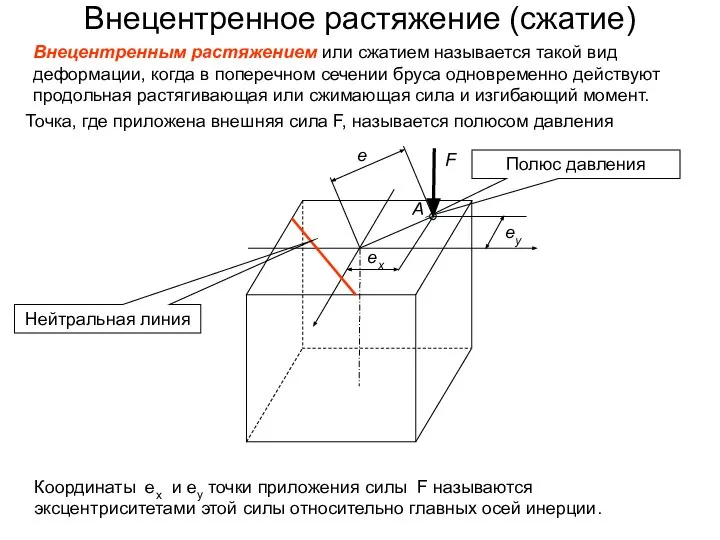
Под сложным сопротивлением подразумевают деформации бруса возникающие
в результате комбинации, в различных сочетаниях, простых видов деформаций: растяжения (сжатия), среза, кручения и изгиба.
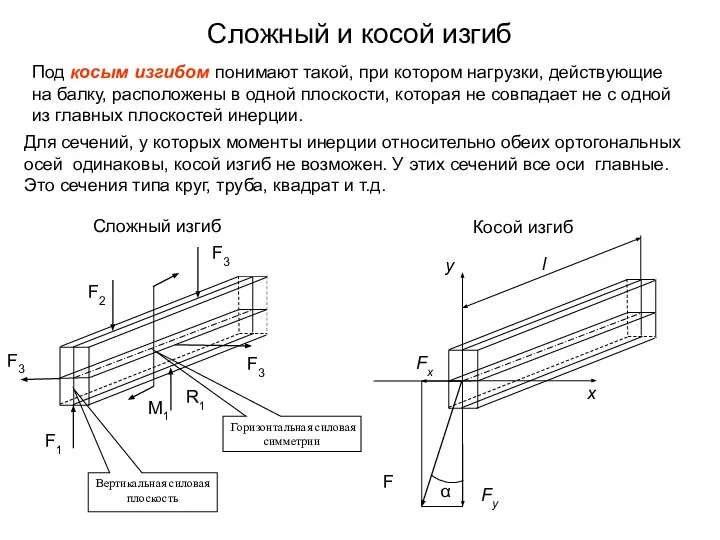
Сложным называется изгиб, вызванный силами или моментами, расположенными в двух и более плоскостях, проходящих через ось балки. Эти плоскости могут, как совпадать, так и не совпадать с главными плоскостями инерции
В том и другом случаях, наиболее удобным решением является приведение к двум плоским изгибам.
Для этого необходимо:
спроектировать все действующие силы на две главные плоскости;
рассмотреть изгиб в каждой из двух главных плоскостей отдельно;
пользуясь принципом независимости действия сил найти суммарные напряжения или деформации.
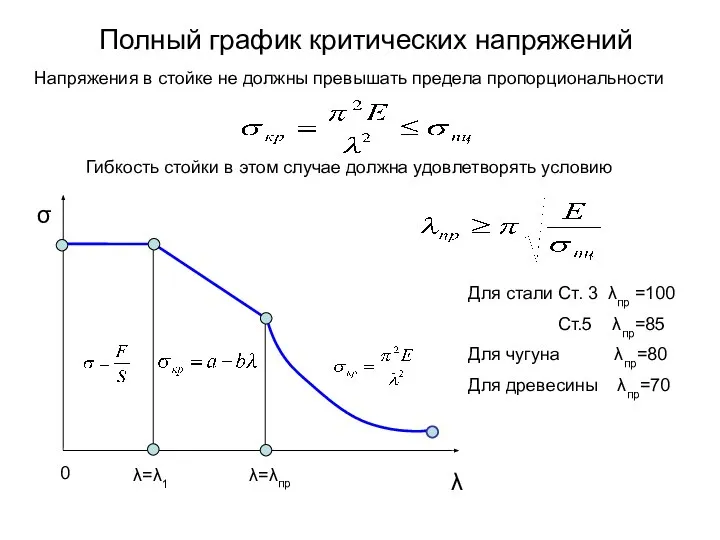
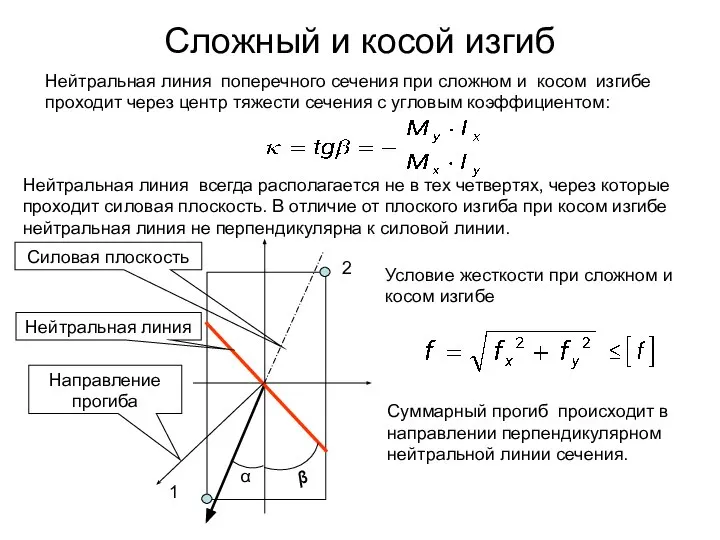
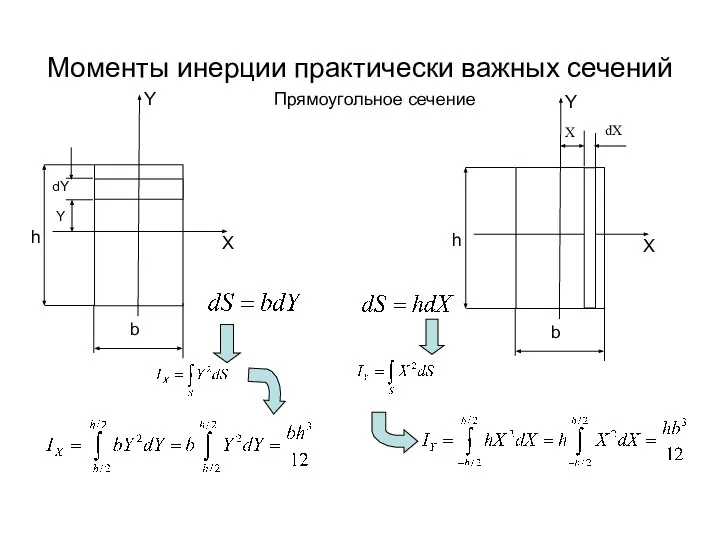
В большинстве случаев в опасной точке поперечного сечения бруса касательные напряжения, либо равны нулю, либо весьма малы по сравнению с нормальными напряжениями, поэтому расчеты на прочность при сложном и косом изгибе ведут с учетом только нормальных напряжений.







 9-1_Компьютерные сети
9-1_Компьютерные сети Методы формирования диаграмм направленности антенн
Методы формирования диаграмм направленности антенн Презентация "Студенческий театр МГУ – наш МОСТ в будущее" - скачать презентации по МХК
Презентация "Студенческий театр МГУ – наш МОСТ в будущее" - скачать презентации по МХК Основы SQL. Описание отношений, доменов, ограничений целостности, представлений данных.
Основы SQL. Описание отношений, доменов, ограничений целостности, представлений данных.  Третий ФОТОФЛЕШМОБ, осенний
Третий ФОТОФЛЕШМОБ, осенний ЯП-алфавит Типы данных выражения операции
ЯП-алфавит Типы данных выражения операции  Признание жилого помещения непригодным для проживания. Аварийное жилое помещение
Признание жилого помещения непригодным для проживания. Аварийное жилое помещение Методическая разработка внеклассного мероприятия с мультемедийным сопровождением, посвященное «Дню смеха» КОНКУРС «Фестиваль
Методическая разработка внеклассного мероприятия с мультемедийным сопровождением, посвященное «Дню смеха» КОНКУРС «Фестиваль Водоэмульсионые краски
Водоэмульсионые краски Гиперактивные дети Презентация Евдокимовой Л.А._
Гиперактивные дети Презентация Евдокимовой Л.А._ Презентация Юридическая клиника при МГУ
Презентация Юридическая клиника при МГУ Пористые заполнители для легких бетонов
Пористые заполнители для легких бетонов Тест по правилам
Тест по правилам Презентация "Управление финансами" - скачать презентации по Экономике
Презентация "Управление финансами" - скачать презентации по Экономике Кәсіпкерліктің ұйымдық-құқықтық нысандары. (Такырып 2)
Кәсіпкерліктің ұйымдық-құқықтық нысандары. (Такырып 2) Внутреннее и внешнее устройство храма и правила поведения в храме
Внутреннее и внешнее устройство храма и правила поведения в храме Якутский народ
Якутский народ Автомобильные диагностические сканеры
Автомобильные диагностические сканеры Структура Киотской Конвенции Презентацию подготовили студенты первого курса ФТД-111 Рекин Сергей, Бобырь Алексей
Структура Киотской Конвенции Презентацию подготовили студенты первого курса ФТД-111 Рекин Сергей, Бобырь Алексей Юзабилити-тестирование в DIRECTUM, или как удивить разработчика
Юзабилити-тестирование в DIRECTUM, или как удивить разработчика Холодильные приборы
Холодильные приборы История спорта
История спорта «Компетентностный подход – это как приведение: все о нем говорят, но мало кто видел». Б. Д. Эльконин
«Компетентностный подход – это как приведение: все о нем говорят, но мало кто видел». Б. Д. Эльконин Twitter : Діалог - валюта бізнесу
Twitter : Діалог - валюта бізнесу Республика Башкортостан
Республика Башкортостан Производные (пользовательские) типы данных
Производные (пользовательские) типы данных Тема проповеди: Секрет 10 конвертов, или Как правильно планировать семейный бюджет
Тема проповеди: Секрет 10 конвертов, или Как правильно планировать семейный бюджет Хронический некалькулёзный холецистит
Хронический некалькулёзный холецистит