ВПМ. Математичне програмування та дослідження операцій. Основні аналітичні властивості задач ЛП. Канонічна форма. (Лекція 2)
Содержание
- 2. Тема 4: Основні аналітичні властивості задач ЛП. Канонічна форма План Загальна постановка задачі ЛП. Форми запису
- 3. Загальна постановка задачі лінійного програмування
- 4. Форми запису задач лінійного програмування За допомогою знака суми Σ. 2. Векторно-матрична форма. 3. Векторна форма.
- 5. Форми запису задач лінійного програмування За допомогою знака суми Σ.
- 6. Форми запису задач лінійного програмування Векторно-матрична форма.
- 7. Форми запису задач лінійного програмування Векторна форма.
- 8. Основні аналітичні властивості розв’язків задач лінійного програмування
- 9. Основні аналітичні властивості розв’язків задач лінійного програмування
- 10. Основні аналітичні властивості розв’язків задач лінійного програмування
- 11. Канонічна форма загальної задачі лінійного програмування
- 12. Правила переходу від загальної задачі лінійного програмування до канонічної Цільову функцію необхідно максимізувати. В системі обмежень
- 13. Правила переходу від загальної задачі лінійного програмування до канонічної Залишкова змінна. Нерівності типу “≤” зазвичай можна
- 14. Правила переходу від загальної задачі лінійного програмування до канонічної
- 15. Приклад зведення задачі ЛП до канонічної форми
- 16. Приклад зведення задачі ЛП до канонічної форми Канонічна форма задачі (4)-(6):
- 17. Основні властивості розв’язків задач лінійного програмування Теорема 1. Множина всіх планів задачі лінійного програмування опукла. Теорема
- 18. Основні властивості розв’язків задач лінійного програмування
- 19. Основні властивості розв’язків задач лінійного програмування
- 20. Тема 5: Лінійне програмування. Симплекс-метод План Симплекс-метод розв'язання задач ЛП. Алгоритм симплекс-методу розв'язання задач ЛП. Правила
- 21. Симплекс-метод розв'язання задач лінійного програмування Симплекс-метод – це поетапна обчислювальна процедура, в основу якої покладено принцип
- 22. Алгоритм симплекс-методу розв'язання задач ЛП Визначення початкового опорного плану задачі ЛП. Побудова симплексної таблиці. Перевірка опорного
- 23. Алгоритм симплекс-методу розв'язання задач ЛП На етапі визначення початкового опорного плану задачі ЛП, після її зведення
- 24. Алгоритм симплекс-методу розв'язання задач ЛП Визначені одиничні лінійно незалежні вектори утворюють базис, і змінні задачі, що
- 25. Алгоритм симплекс-методу розв'язання задач ЛП
- 26. Алгоритм симплекс-методу розв'язання задач ЛП
- 27. Алгоритм симплекс-методу розв'язання задач ЛП
- 28. Алгоритм симплекс-методу розв'язання задач ЛП
- 29. Правила перебудови симплекс-таблиці за методом Жорданa-Гаусса 1. Розв’язувальний (напрямний) рядок необхідно поділити на розв’язувальний елемент і
- 30. Правило прямокутника перебудови симплекс-таблиці
- 31. Варіанти розв'язку задачі ЛП симплекс-методом
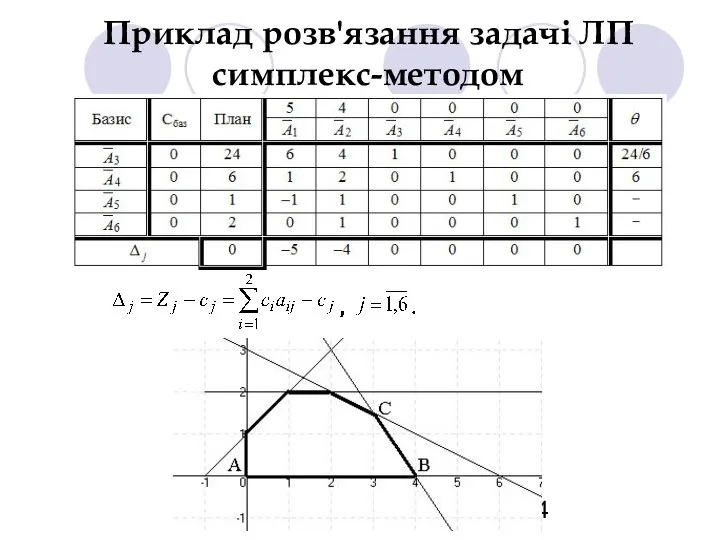
- 32. Приклад розв'язання задачі ЛП симплекс-методом
- 33. Приклад розв'язання задачі ЛП симплекс-методом
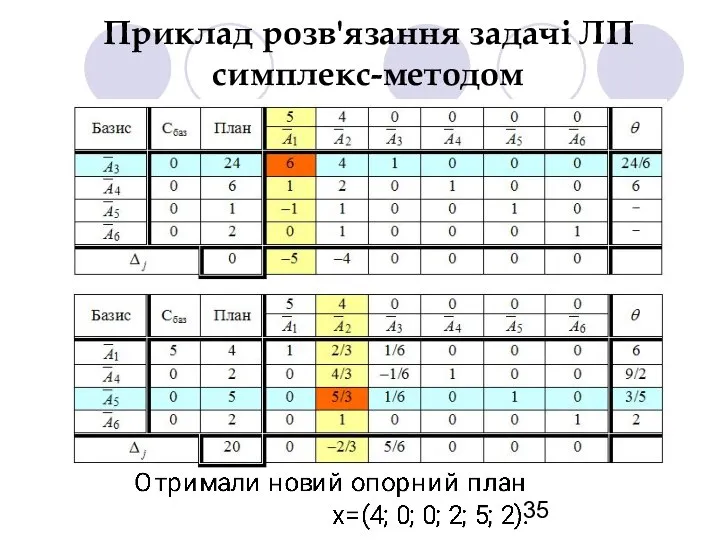
- 34. Приклад розв'язання задачі ЛП симплекс-методом
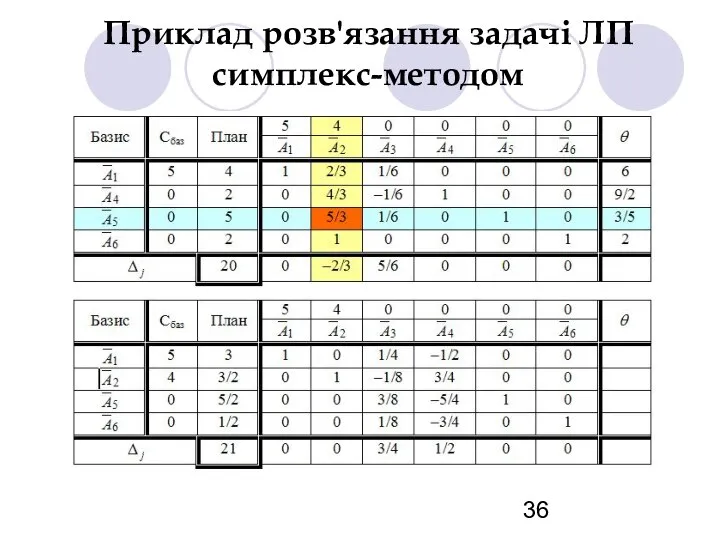
- 35. Приклад розв'язання задачі ЛП симплекс-методом
- 36. Приклад розв'язання задачі ЛП симплекс-методом
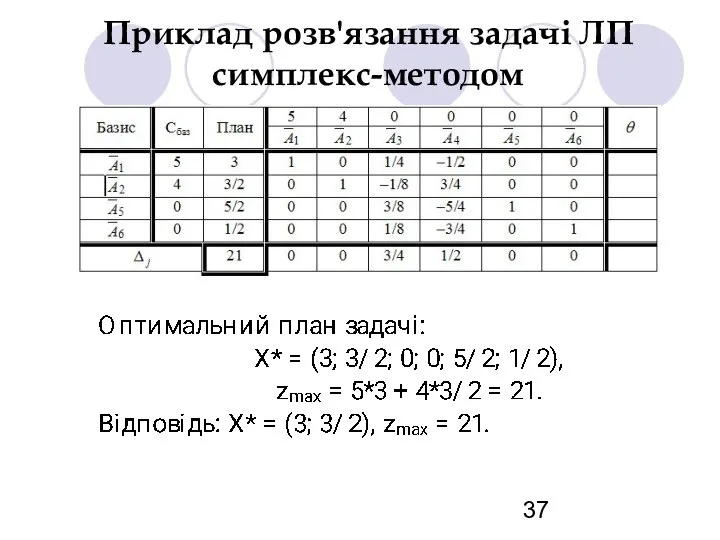
- 37. Приклад розв'язання задачі ЛП симплекс-методом
- 38. Тема 6: Двоїстість у задачах лінійного програмування План Правила побудови двоїстої задачі лінійного програмування. Приклад побудови
- 39. Постановка задачі лінійного програмування (пряма задача) Кожній задачі ЛП відповідає двоїста, що формується за допомогою певних
- 40. Економічний зміст прямої задачі
- 41. Постановка задачі лінійного програмування (двоїста задача)
- 42. Економічний зміст двоїстої задачі
- 43. Постановка пари двоїстих задач у матрично-векторній формі
- 44. Правила побудови двоїстої задачі лінійного програмування 1. Кожному обмеженню прямої задачі відповідає змінна двоїстої задачі. Кількість
- 45. Правила побудови двоїстої задачі лінійного програмування 4. Коефіцієнтами при змінних у цільовій функції двоїстої задачі є
- 46. Правила побудови двоїстої задачі лінійного програмування 7. Якщо змінній двоїстої задачі відповідає обмеження прямої задачі у
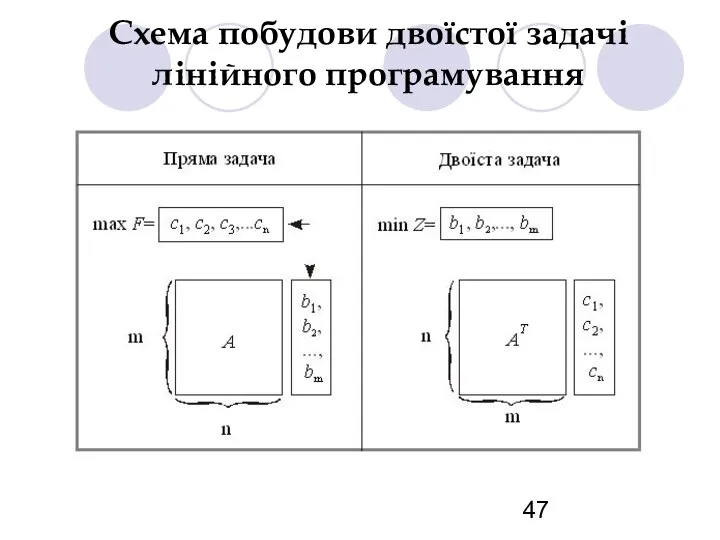
- 47. Схема побудови двоїстої задачі лінійного програмування
- 48. Приклад побудови двоїстої задачі лінійного програмування
- 49. Приклад побудови двоїстої задачі лінійного програмування
- 50. Основні теореми двоїстості
- 51. Основні теореми двоїстості (І теорема двоїстості)
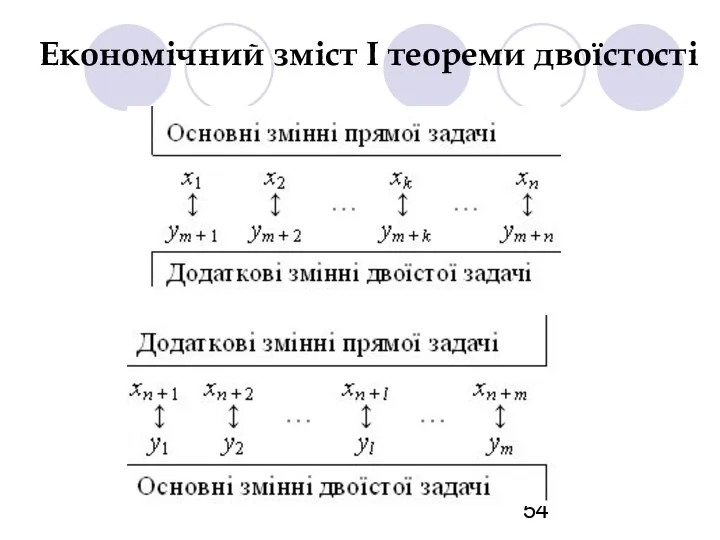
- 52. Економічний зміст І теореми двоїстості
- 53. Економічний зміст І теореми двоїстості
- 54. Економічний зміст І теореми двоїстості
- 55. Основні теореми двоїстості (наслідок з І теореми двоїстості)
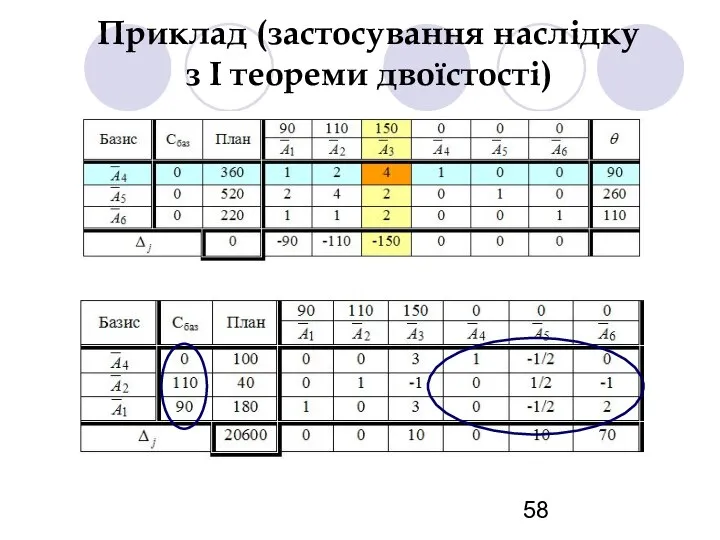
- 56. Приклад (застосування наслідку з І теореми двоїстості) Ціна одиниці продукції видів А, В і С дорівнює
- 57. Приклад (застосування наслідку з І теореми двоїстості)
- 58. Приклад (застосування наслідку з І теореми двоїстості)
- 59. Приклад (застосування наслідку з І теореми двоїстості)
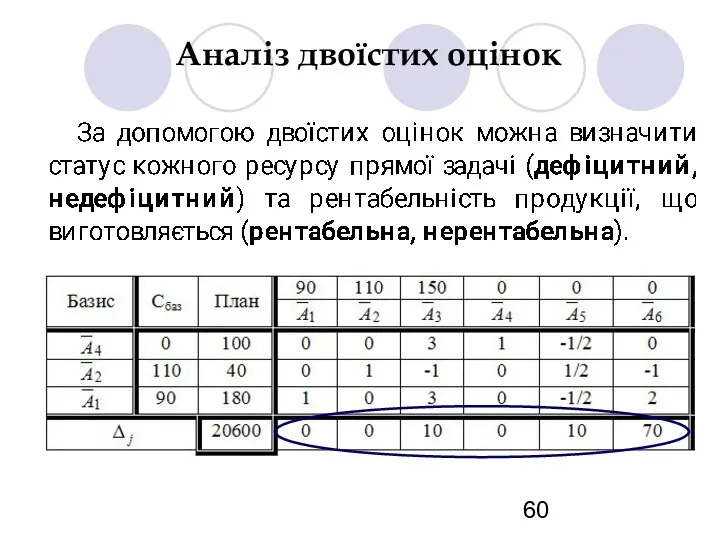
- 60. Аналіз двоїстих оцінок
- 61. Основні теореми двоїстості (ІІ теорема двоїстості)
- 62. Економічний зміст ІІ теореми двоїстості
- 63. Економічний зміст ІІ теореми двоїстості
- 64. Наслідок ІІ теореми двоїстості
- 65. Приклад (застосування наслідку з ІІ теореми двоїстості)
- 66. Основні теореми двоїстості (ІІІ теорема двоїстості)
- 67. Економічний зміст ІІІ теореми двоїстості
- 68. Аналіз задачі на чутливість
- 69. Аналіз задачі на чутливість. Алгоритм 1. Формулюємо математичну модель задачі лінійного програмування та двоїсту до неї.
- 71. Скачать презентацию




























































 Тема 6
Тема 6  Разработка техпроцесса восстановления зубчатого колеса ткацкого станка
Разработка техпроцесса восстановления зубчатого колеса ткацкого станка Постреляционные, объектные модели данных
Постреляционные, объектные модели данных Конгресс Соединенных Штатов Америки
Конгресс Соединенных Штатов Америки Экология
Экология  Электротехника и электроника. Основные определения
Электротехника и электроника. Основные определения Іменник
Іменник  Физиология эндокринной системы
Физиология эндокринной системы Осанка. Дефекты осанки. Упражнения для формирования правильной осанки
Осанка. Дефекты осанки. Упражнения для формирования правильной осанки ПСОРИАТИЧЕСКИЙ АРТРИТ Врач-дерматовенеролог Махмуд Асиф
ПСОРИАТИЧЕСКИЙ АРТРИТ Врач-дерматовенеролог Махмуд Асиф Tema_4
Tema_4 Җәя кую очраклары
Җәя кую очраклары Консерватизм как политическая идеология
Консерватизм как политическая идеология Мир развлечений
Мир развлечений Средние величины и показатели вариации
Средние величины и показатели вариации Презентация "Сбереженная капля море спасет" - скачать презентации по Экономике
Презентация "Сбереженная капля море спасет" - скачать презентации по Экономике Профессиограмма ЮРИСТА
Профессиограмма ЮРИСТА Особенности распространения возбуждения в ЦНС
Особенности распространения возбуждения в ЦНС  Александр Трифонович Твардовский. Русский советский писатель и поэт, журналист, военный корреспондент
Александр Трифонович Твардовский. Русский советский писатель и поэт, журналист, военный корреспондент Развитие науки и образования в России в начале 18 века
Развитие науки и образования в России в начале 18 века 3D-сканеры и 3D-принтеры
3D-сканеры и 3D-принтеры Демократия. Местное самоуправление в РФ
Демократия. Местное самоуправление в РФ Столицы стран мира
Столицы стран мира Проект организации и планирования выполнения тахеометрической съемки для последующего строительства водоограждающей дамбы
Проект организации и планирования выполнения тахеометрической съемки для последующего строительства водоограждающей дамбы Улс төрийн нам Улс төрийн нам
Улс төрийн нам Улс төрийн нам Физиотерапия Область клинической медицины, изучающая лечебные свойства физических факторов и разрабатывающая методы их п
Физиотерапия Область клинической медицины, изучающая лечебные свойства физических факторов и разрабатывающая методы их п НОЦИЦЕПЦИЯ Рецепция боли
НОЦИЦЕПЦИЯ Рецепция боли  Анализ рядов динамики
Анализ рядов динамики