Содержание
- 2. Максвелловский закон распределения по скоростям и все вытекающие следствия справедливы только для газа в равновесной системе.
- 3. Формула Максвелла для относительных скоростей Для решения многих задач удобно использовать формулу Максвелла, где скорость выражена
- 4. 4. Барометрическая формула Рассмотрим ещё один вероятный закон очень важно. Атмосферное давление на какой-либо высоте h
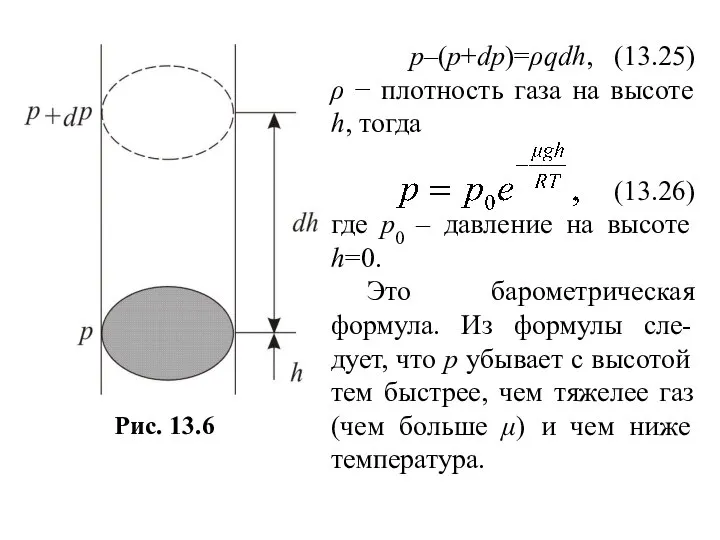
- 5. p–(p+dp)=ρqdh, (13.25) ρ − плотность газа на высоте h, тогда (13.26) где р0 – давление на
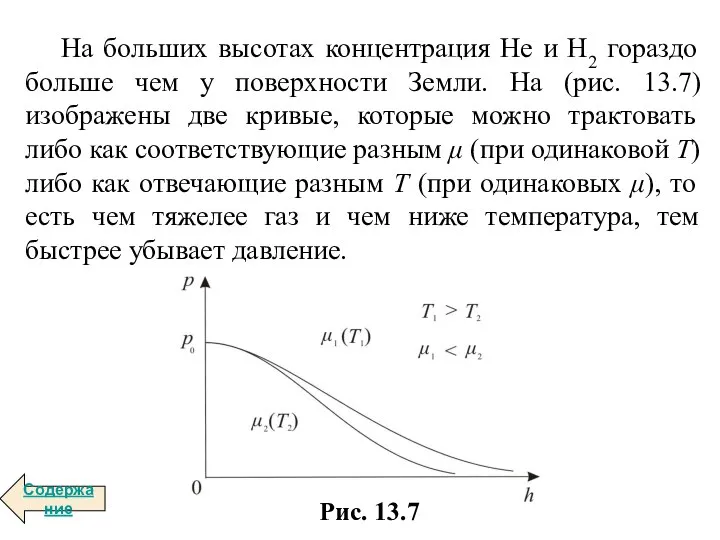
- 6. На больших высотах концентрация Не и Н2 гораздо больше чем у поверхности Земли. На (рис. 13.7)
- 7. 5. Распределение Больцмана Нам известна формула р=nkT – это основное уравнение МКТ (p0=nkT), заменим p и
- 8. С уменьшением температуры число молекул на высотах, отличных от нуля убывает. При Т=0 тепловое движение прекращается,
- 10. Больцман доказал, что соотношение (13.29) справедливо не только в потенциальном поле сил гравитации, но и в
- 11. 6. Закон распределения Максвелла-Больцмана Вначале лекции мы с вами получили выражение для распределения молекул по скоростям
- 12. (13.31) где dnWк – число молекул имеющих кинетическую энергию поступательного движения, заключённую в интервале от Wк
- 13. Итак, закон Максвелла даёт распределение частиц по значениям кинетической энергии, а закон Больцмана – даёт распределение
- 14. Обозначим W – полная энергия равна Wп+Wк (13.34) Это и есть закон распределения Максвелла-Больцмана, где n0
- 15. В последнем выражении, потенциальная и кинетическая энергии, а следовательно и полная энергия W могут принимать непрерывный
- 16. В (13.36) N – полное число частиц в рассматриваемой системе. Тогда окончательное выражение распределения Больцмана для
- 17. 7. Распределение Бозе–Эйнштейна, Ферми–Дирака Если у нас имеется термодинамическая система состоящая из N частиц, энергии которых
- 18. 1. Распределение Бозе – Эйнштейна: (13.38) 2. Распределение Ферми – Дирака: (13.39) Первая формула описывает квантовые
- 20. Скачать презентацию















 Виды кровельного покрытия
Виды кровельного покрытия Основы XML-технологий
Основы XML-технологий Землеустройство при совершенствовании территориальной организации сельских поселений на примере Михайловского района
Землеустройство при совершенствовании территориальной организации сельских поселений на примере Михайловского района Доклад по подведению итогов работы. Изменение технологии сокращенного УРГ станции Астрахань
Доклад по подведению итогов работы. Изменение технологии сокращенного УРГ станции Астрахань Современные строительные материалы для отделки фасадов
Современные строительные материалы для отделки фасадов CRM On Demand Владимир Карагиоз
CRM On Demand Владимир Карагиоз  Квантовая гипотеза и формула де Бриля
Квантовая гипотеза и формула де Бриля  Народные зимние праздники (интеллектуальная игра для 5-6 классов)
Народные зимние праздники (интеллектуальная игра для 5-6 классов) Рынок труда и заработной платы
Рынок труда и заработной платы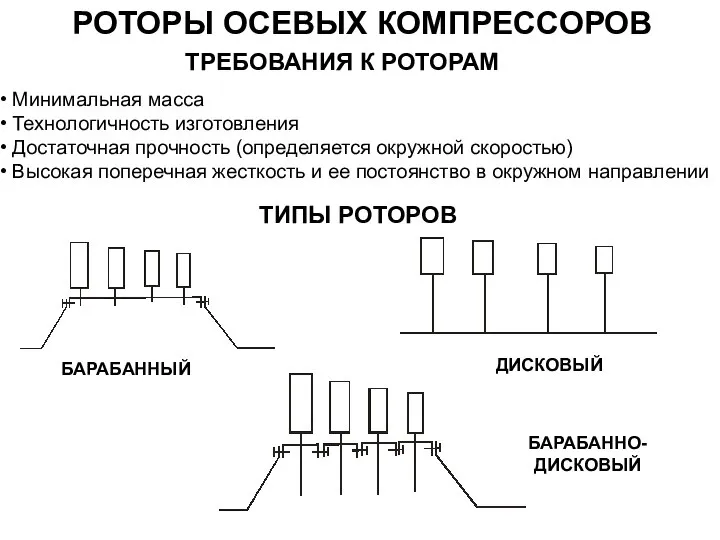 Роторы осевых компрессоров. Требования к роторам
Роторы осевых компрессоров. Требования к роторам Объекты гражданских прав
Объекты гражданских прав  Профориентационное занятие по курсу Г.В.Резапкиной Презентация подготовлена педагогом-психологом ГОУ ЦО № 771, г.Москвы ДЕТ
Профориентационное занятие по курсу Г.В.Резапкиной Презентация подготовлена педагогом-психологом ГОУ ЦО № 771, г.Москвы ДЕТ Презентация на тему Первичная обработка овощей
Презентация на тему Первичная обработка овощей  Презентация на тему: “Война и право” Презентацию подготовил: ученик 10класса Дударев Р. Учитель: Левадная И.М
Презентация на тему: “Война и право” Презентацию подготовил: ученик 10класса Дударев Р. Учитель: Левадная И.М  Измерение микрометрическим инструментом
Измерение микрометрическим инструментом Если вы никак не можете себя заставить работать
Если вы никак не можете себя заставить работать Соединения галогенов
Соединения галогенов Красный крест
Красный крест  Олег Монгол
Олег Монгол Презентация на тему "Школьная жизнь" - скачать презентации по Педагогике
Презентация на тему "Школьная жизнь" - скачать презентации по Педагогике Литографии Евгения Ивановича Чарушина
Литографии Евгения Ивановича Чарушина Мастер - класс « Рисование контурами»
Мастер - класс « Рисование контурами»  Жилищный найм
Жилищный найм Лекция № 9 на тему:
Лекция № 9 на тему:  История возникновения Алгебры. Выполнила : Артамонова Мария.
История возникновения Алгебры. Выполнила : Артамонова Мария. Современные концепции построения тренировочных макроциклов
Современные концепции построения тренировочных макроциклов Системы классификации информации
Системы классификации информации звездный час - презентация для начальной школы_
звездный час - презентация для начальной школы_