Содержание
- 2. Фиктивная переменная (ФП) – это переменная, которая принимает два различных значения. Эти различные значения могут быть
- 3. ФП используются для ввода в модель регрессии качественных и категориальных факторов.
- 4. ФП для качественного фактора, принимающего два значения. Модель без взаимодействия.
- 5. На фактор Y, кроме количественных факторов X2, X3, …, Xk, воздействует качественный фактор, который принимает два
- 6. Чтобы учесть влияние этого фактора, в модель вводят фиктивный фактор D. для объектов, на которых качественный
- 7. Или можно наоборот: для …не А для … А
- 8. Модель тогда имеет вид: Y = β1+ β2*X2 + … + βk*Xk + δ*D + u
- 9. Y = β1+ β2*X2 + … + βk*Xk + δ*D + u Интерпретация коэффициента δ: при
- 10. Y = β1+ β2*X2 + … + βk*Xk + δ*D + u Проверяя по t-тесту значимость
- 11. ПРИМЕР 1. Y – среднемесячное потребление семьи, в рублях. X – среднемесячный доход семьи, в рублях.
- 12. Вводим ФП D. Пусть D=1 для семей из сельской местности и D=0 для городских семей. Модель:
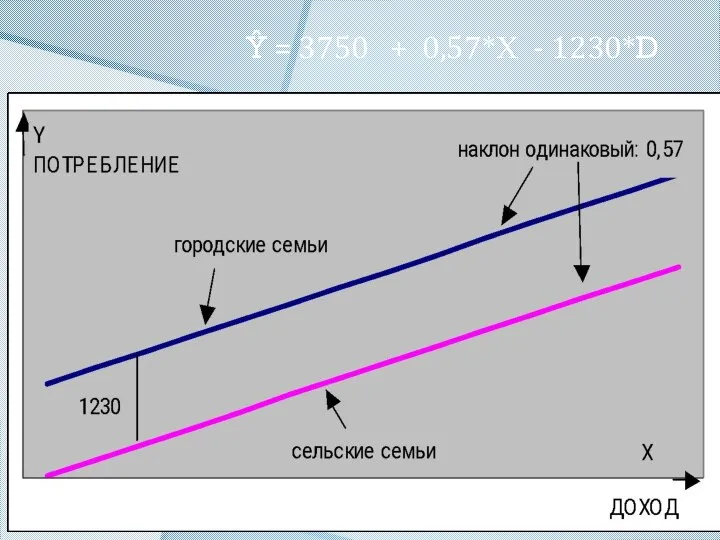
- 13. Ŷ = 3750 + 0,57*Х - 1230*D (1119) (0.22) (349) Проверяем гипотезу: H0: δ = 0
- 14. Сельские семьи тратят на потребление в среднем на 1230 рублей меньше, чем городские семьи, имеющие такой
- 15. Замечание: в теоретической модели предполагается, что на изменение дохода городские и сельские семьи реагируют одинаково. При
- 16. Ŷ = 3750 + 0,57*Х - 1230*D Можно получить уравнения отдельно для сельских и городских семей.
- 17. Ŷ = 3750 + 0,57*Х - 1230*D
- 18. II. ФП для качественного фактора, принимающего более 2-х значений. Модель без взаимодействия.
- 19. Качественный фактор принимает p значений (имеет p категорий), и p > 2.
- 20. Можно было бы ввести одну ФП, принимающую p различных значений. Но в этом случае трудно интерпретировать
- 21. Вводят p ФП, D1, D2, … , Dp, каждая из которых принимает два значения: 0 и
- 22. Одна из ФП объявляется эталонной и в модель не включается. Т. е. в модель включаются не
- 23. Если, например, эталонной выбрали ФП D1, то модель имеет вид: Y = β1+ β2*X2 + …
- 24. III. ФП для нескольких качественных факторов. Модель без взаимодействия.
- 25. На Y влияют несколько качественных факторов. Тогда в модель вводят соответствующее количество фиктивных переменных.
- 26. ПРИМЕР 5. Y – з/п работника Х – стаж работника З\п зависит также от уровня образования
- 27. Для уровня образования, как и выше, вводят 4-е ФП D1, D2, D3, D4. Пусть, например, эталонной
- 28. Модель: Y = β1+ β2*X + δ1*D1 + δ2*D2 + δ4*D4 + π*П + u.
- 29. IV. Модель со взаимодействием. ФП для коэффициентов наклона.
- 30. Для простоты будем рассматривать качественный фактор с 2-я категориями (значениями).
- 31. В модели без взаимодействия Y = β1+ β2*X + δ*D + u ФП D влияет только
- 32. Т. е. считается, что качественный фактор: (а) влияет на значение Y для разных категорий объектов, у
- 33. В модели со взаимодействием предположение (б) снимается. Допускается, что Y может по-разному реагировать на изменения Х
- 34. Модель со взаимодействием: Y = β1 + β2* X + δ*D + γ*D*X + u. Ее
- 35. V. Модель со взаимодействием. Взаимодействие между ФП
- 36. ПРИМЕР 8. Y – з/п сотрудника в рублях, Х – стаж сотрудника, в годах. На з/п
- 37. Вводим ФП П – «пол»: П = 0 для женщин, П = 1 для мужчин. Вводим
- 38. Модель: Y = α + β*X + δ*П + γ*E + λ*П*Е + u. Перепишем эту
- 39. Y = α + β*X + (δ + λ*E)*П + γ*Е + u. Т. е. при
- 40. Модель: Y = α + β*X + δ*П + γ*E + λ*П*Е + u. Эту модель
- 41. Y = α + β*X + δ*П + (γ + λ*П)*Е + u. Т.е. при одинаковом
- 42. Y = α + β*X + δ*П + γ*E + λ*П*Е + u. Примечание. Значимость коэффициента
- 43. Критерий Чоу В практике нередки случаи, когда имеются две выборки пар значений зависимой и объясняющих переменных
- 44. При достаточных объемах выборок можно было, например, построить интервальные оценки параметров регрессии по каждой из выборок
- 45. В критерии {тесте) Г. Чоу эти трудности в существенной степени преодолеваются. Алгоритм теста Чоу: 1.По каждой
- 48. Скачать презентацию






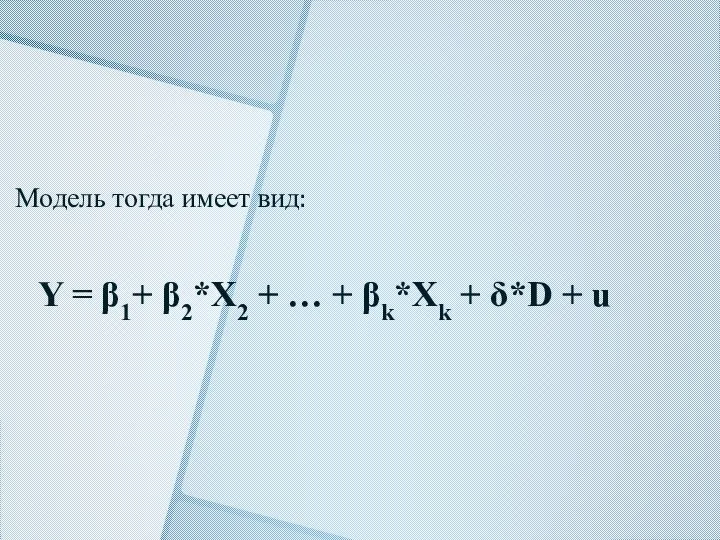





































 Теория игр
Теория игр Себестоимость продукции и прибыль предприятия
Себестоимость продукции и прибыль предприятия Хозяйство России
Хозяйство России Национальный союз производителей говядины. Российский рынок КРС и мяса: состояние и прогнозы
Национальный союз производителей говядины. Российский рынок КРС и мяса: состояние и прогнозы Виды затрат и их экономическое значение
Виды затрат и их экономическое значение СНГ: проблемы и перспективы дальнейшего развития
СНГ: проблемы и перспективы дальнейшего развития Україна - Швеція
Україна - Швеція Меркосур. Эффекты от латиноамериканского ТС
Меркосур. Эффекты от латиноамериканского ТС Региональные союзы
Региональные союзы Экономическое регулирование деятельности автотуризма
Экономическое регулирование деятельности автотуризма Распределение рисков и стратегия доставки
Распределение рисков и стратегия доставки Экономика. Вопросы кодификатора
Экономика. Вопросы кодификатора Основные понятия и особенности макроэкономического анализа
Основные понятия и особенности макроэкономического анализа Актуальные проблемы экономики таможенного дела. Лекция № 2
Актуальные проблемы экономики таможенного дела. Лекция № 2 Инфляция и семейная экономика
Инфляция и семейная экономика Транснациональные компании
Транснациональные компании Международное предпринимательство (задачи, часть 2)
Международное предпринимательство (задачи, часть 2) Регулирование рыночной экономики
Регулирование рыночной экономики Презентация Типология Политических режимов
Презентация Типология Политических режимов Технология продажи
Технология продажи Об основных направлениях повышения эффективности бюджетных расходов в субъектах Российской Федерации
Об основных направлениях повышения эффективности бюджетных расходов в субъектах Российской Федерации Экономическая теория. Теория денег. (Тема 6)
Экономическая теория. Теория денег. (Тема 6) Зачем создаются фирмы. Виды фирм
Зачем создаются фирмы. Виды фирм Викторина по энергосбережению
Викторина по энергосбережению Научно-техническая революция (НТР)
Научно-техническая революция (НТР) Сутність, завдання та рівні товарної політики підприємства
Сутність, завдання та рівні товарної політики підприємства Рынок труда в сфере юриспруденции
Рынок труда в сфере юриспруденции Стратегия развития Новосибирского ГАУ
Стратегия развития Новосибирского ГАУ