Содержание
- 2. In particular, you will Determine why S-curves are necessary Review the ideal S-curve. Consider constant acceleration
- 3. Why S-curves? Reviewing the trapezoidal trajectory profile in speed v, we examine points 1, 2, 3,
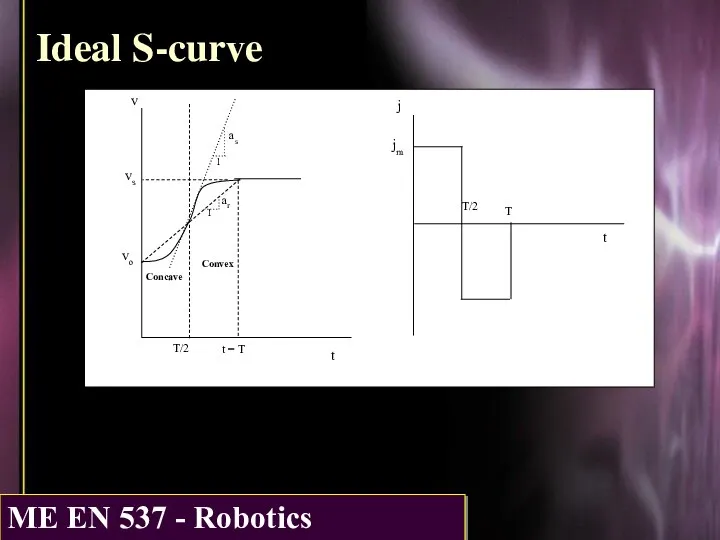
- 4. Ideal S-curve t t = T vo vs v 1 as ar 1 Concave Convex t
- 5. Ideal S-curve equations The form assumed for the S-curve velocity profile is v(t) = co +
- 6. Concave period The concave conditions are v(0) = vo a(0) = 0 a(T/2) = as j(0)
- 7. Concave period Applying the initial and final conditions, we get the equations for s (position), v,
- 8. Ideal S-curve observations If we let Δv = vs - vo and define ar = Δv/T
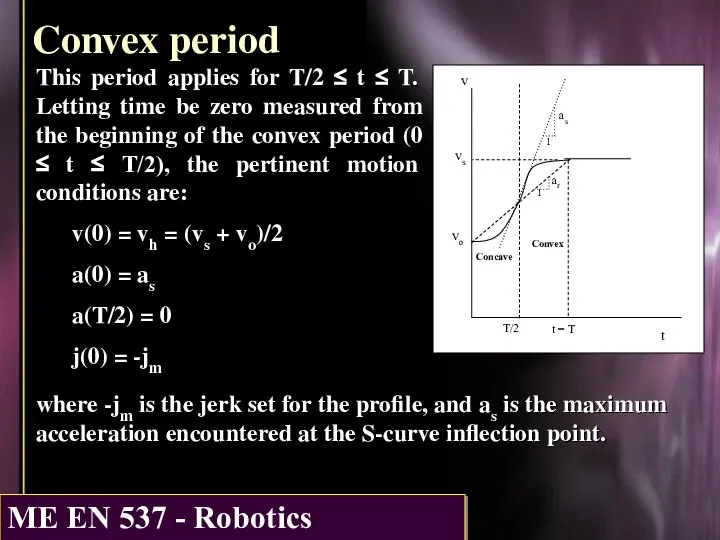
- 9. Convex period This period applies for T/2 ≤ t ≤ T. Letting time be zero measured
- 10. Convex period Applying the initial and final conditions, we get the equations for s (position), v,
- 11. Distance traversed Adding in the distance at the halfway point gives the total distance traversed in
- 12. Max jerk transitions An ideal S-curve cannot transition smoothly between any speed change using a specified
- 13. Max jerk transitions Given a jerk jm, a starting speed vo, and the ending speed vs,
- 14. Speed transitions If v1 > v2 (overlap), we can determine an intermediate transition point using speed
- 15. Speed transitions
- 16. Speed transitions The pertinent equations are: vo + ao Tt + jm Tt 2/2 = vs-
- 17. S-curve with linear period If v1
- 18. S-curve with linear period Motion conditions: Phase 1 - Concave Phase 2 – Linear Phase 3
- 19. S-curve with linear period Phase 1 – Concave motion conditions: s(t) = vo t + jm
- 20. S-curve with linear period Phase 2 – Linear motion conditions: s(t) = v1 t + as
- 21. S-curve with linear period Phase 3 – Convex motion conditions: s(t) = v2 t + as
- 22. S-curve context How is the S-curve applied in the real world? Robots and machine tools are
- 24. Скачать презентацию



















 Реактивное движение
Реактивное движение Принцип действия радиотелефонной связи. Радиовещание и телевидение
Принцип действия радиотелефонной связи. Радиовещание и телевидение  Презентация на тему: Тайна черной дыры!
Презентация на тему: Тайна черной дыры! Варианты самостоятельной работы
Варианты самостоятельной работы Динамика материальной точки. Лекция 3
Динамика материальной точки. Лекция 3 Презентация по физике "«Механическое движение тела»" - скачать
Презентация по физике "«Механическое движение тела»" - скачать  Пьезопреобразователи. Методы расчета. (Раздел 3)
Пьезопреобразователи. Методы расчета. (Раздел 3) История развития материаловедения
История развития материаловедения Ток күші. Амперметр. Электр кернеуі. Вольтметр
Ток күші. Амперметр. Электр кернеуі. Вольтметр Дифракция электромагнитной волны
Дифракция электромагнитной волны Даими магнитларның магнит кыры. дайм Жирнең магнит кыры
Даими магнитларның магнит кыры. дайм Жирнең магнит кыры Механизмы переноса тепла: теплопроводность, конвекция, излучение
Механизмы переноса тепла: теплопроводность, конвекция, излучение Реология. Течение и свойства жидкостей
Реология. Течение и свойства жидкостей Основы специальной теории относительности
Основы специальной теории относительности Прозрачный люминесцентный солнечный концентратор
Прозрачный люминесцентный солнечный концентратор Закон Кулона
Закон Кулона Использование энергии
Использование энергии Одномерные изоэнтропные движения газа
Одномерные изоэнтропные движения газа Объяснение электрических явлений
Объяснение электрических явлений Рівномірний рух по колу
Рівномірний рух по колу Фотоэффект. Теория фотоэффекта
Фотоэффект. Теория фотоэффекта Введение в теорию конечных элементов
Введение в теорию конечных элементов Звуковые волны
Звуковые волны Вечный двигатель на капиллярном притяжение
Вечный двигатель на капиллярном притяжение Методы изучения кинетики электродных процессов
Методы изучения кинетики электродных процессов Техническое облуживание АКПП с гидравлическим приводом
Техническое облуживание АКПП с гидравлическим приводом Проверка домашнего задания тест
Проверка домашнего задания тест Плотность . Решение задач. Урок физики в 7 классе. Учитель Кононова Е.Ю.
Плотность . Решение задач. Урок физики в 7 классе. Учитель Кононова Е.Ю.