Содержание
- 2. Гравитационные волны (жидкость неограниченной глубины) В современной физике волны – краеугольный камень в изучении линейных (а
- 3. Гравитационные волны – волны на поверхности воды (рис. 1), для существования которых фундаментальную роль играет сила
- 4. Исходные допущения: Жидкость неограниченно большой глубины −∞ Отклонения поверхности ζ настолько малы, что им сопутствуют малые
- 5. Производимая волной разность давлений в точках границы z=ζ должна отсутствовать независимо от вида возмущений (граница с
- 6. В итоге имеем решение вида: Вывод дисперсионного соотношения По условиям возбуждения величины известны. Волновое число k
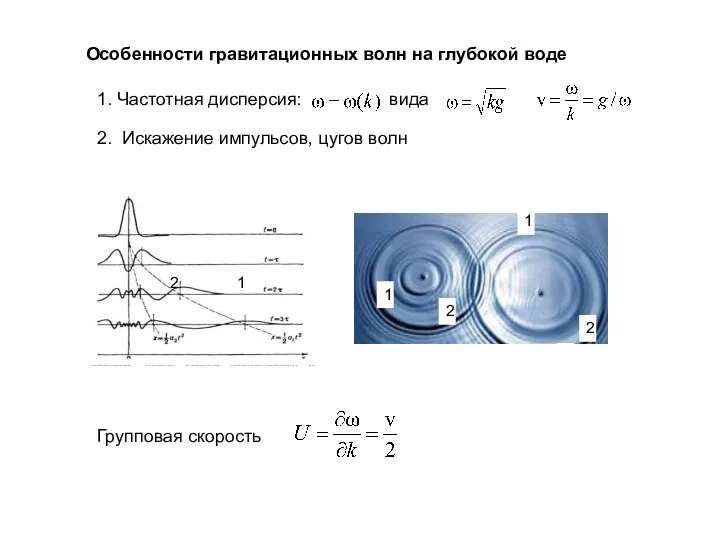
- 7. Особенности гравитационных волн на глубокой воде 1. Частотная дисперсия: вида 2. Искажение импульсов, цугов волн 1
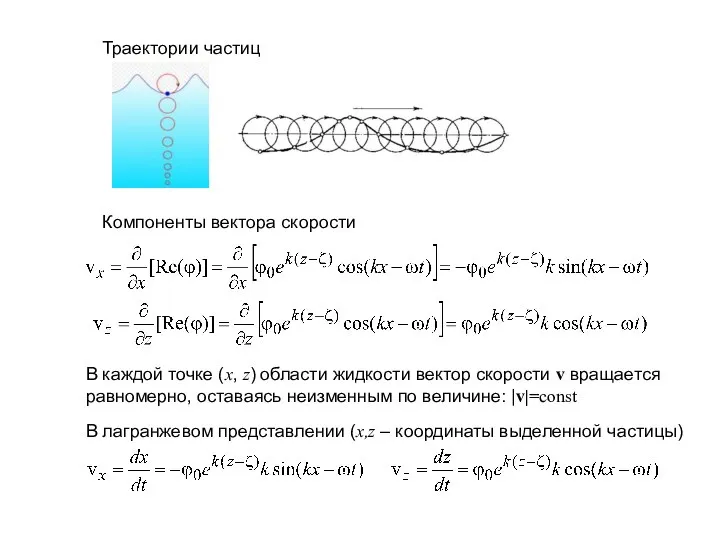
- 8. Траектории частиц Компоненты вектора скорости В каждой точке (x, z) области жидкости вектор скорости v вращается
- 9. Уравнения движения частицы жидкости в параметрической форме. Показывают, что частицы жидкости в гравитационной волне описывают вокруг
- 10. Адиабатическая связь p(ρ) − следствие обычно быстрого протекания акустических процессов, когда теплопередача между участками среды практически
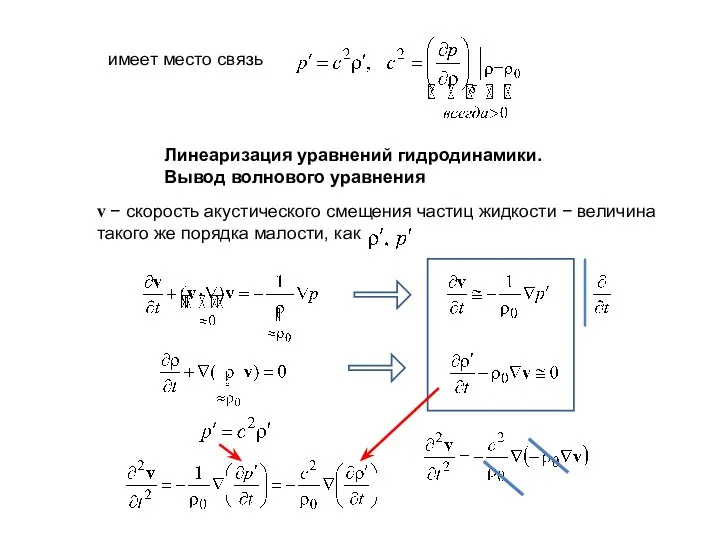
- 11. имеет место связь Линеаризация уравнений гидродинамики. Вывод волнового уравнения v − скорость акустического смещения частиц жидкости
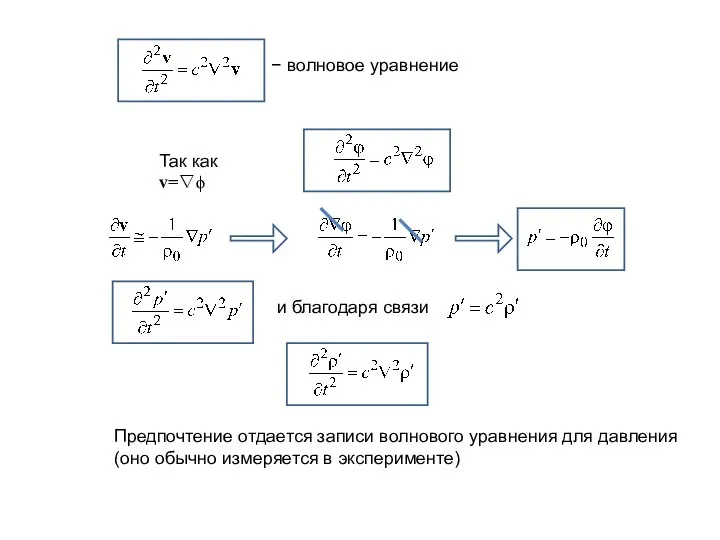
- 12. − волновое уравнение Так как v=∇ϕ и благодаря связи Предпочтение отдается записи волнового уравнения для давления
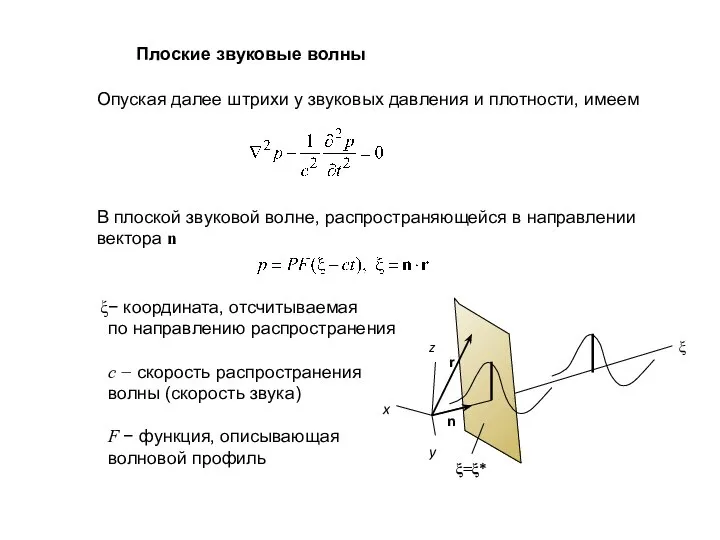
- 13. Плоские звуковые волны Опуская далее штрихи у звуковых давления и плотности, имеем В плоской звуковой волне,
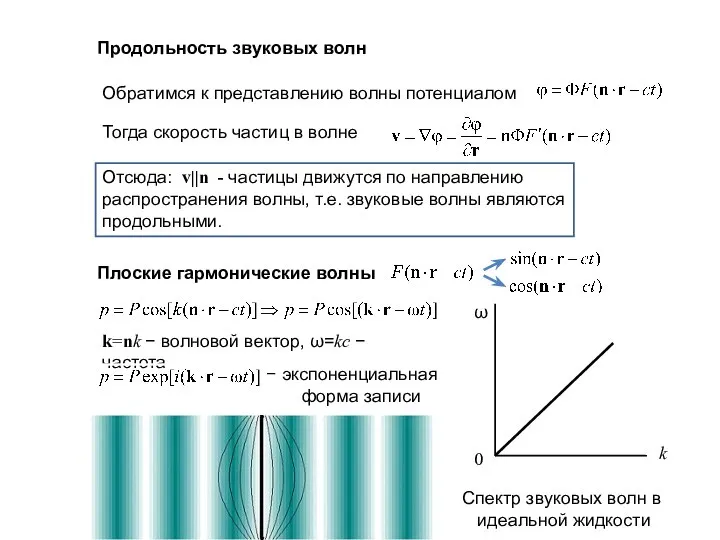
- 14. Продольность звуковых волн Обратимся к представлению волны потенциалом Тогда скорость частиц в волне Отсюда: v||n -
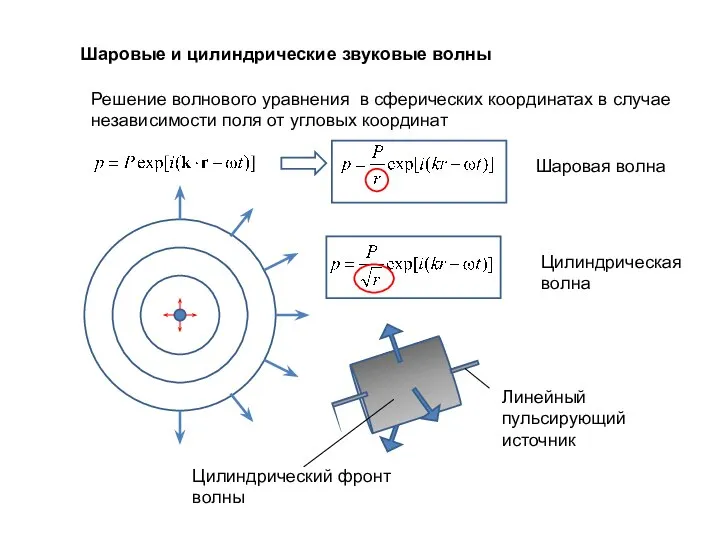
- 15. Шаровые и цилиндрические звуковые волны Решение волнового уравнения в сферических координатах в случае независимости поля от
- 17. Скачать презентацию







 Равновесие при радиоактивном распаде. (Лекция 2)
Равновесие при радиоактивном распаде. (Лекция 2) Сейсмическая стратиграфия
Сейсмическая стратиграфия Биофизика мембран Транспорт веществ. (Лекция 6)
Биофизика мембран Транспорт веществ. (Лекция 6) «Путешествие в страну любознательных физиков»
«Путешествие в страну любознательных физиков» Физические характеристики вибрации
Физические характеристики вибрации Сложение гармонических колебаний. Волновые процессы. Сложение взаимно перпендикулярных колебаний
Сложение гармонических колебаний. Волновые процессы. Сложение взаимно перпендикулярных колебаний Оптика. ( Источники, отражение и преломление света) Подготовил: Ученик МОУ лицея № 18 Кондратов Алексей
Оптика. ( Источники, отражение и преломление света) Подготовил: Ученик МОУ лицея № 18 Кондратов Алексей  Диэлектриктегі физикалық процесс. Диэлектрлік шығындар
Диэлектриктегі физикалық процесс. Диэлектрлік шығындар ЦАП Цифро-аналоговый преобразователь
ЦАП Цифро-аналоговый преобразователь Внутренняя энергия
Внутренняя энергия  Установка дополнительного уплотнения разъема на аккумуляторную батарею. Инструкция
Установка дополнительного уплотнения разъема на аккумуляторную батарею. Инструкция Резонанс
Резонанс Характеристики датчиков
Характеристики датчиков Характеристика и технология производства основных катализаторов нефтепереработки
Характеристика и технология производства основных катализаторов нефтепереработки Великие ученые прошлого
Великие ученые прошлого  Нелинейно - оптические эффекты в волоконных световодах (лекция 8)
Нелинейно - оптические эффекты в волоконных световодах (лекция 8) Абсолютно твёрдое тело
Абсолютно твёрдое тело Презентация ТРЕТИЙ ЗАКОН НЬЮТОНА Законы движения
Презентация ТРЕТИЙ ЗАКОН НЬЮТОНА Законы движения Понятие движение
Понятие движение Обработка экспериментальных данных. Часть 1
Обработка экспериментальных данных. Часть 1 Механизм старения масел
Механизм старения масел Принцип работы бесщеточного двигателя постоянного тока. Простейшие схемы двигателей. (Лекция 2)
Принцип работы бесщеточного двигателя постоянного тока. Простейшие схемы двигателей. (Лекция 2) Определение расчетного коэффициента сцепления локомотива
Определение расчетного коэффициента сцепления локомотива Планетарная (ядерная) модель атома Атом – микрочастица, состоящая из положительно заряженного ядра и окружающих его электронов
Планетарная (ядерная) модель атома Атом – микрочастица, состоящая из положительно заряженного ядра и окружающих его электронов Измельчение в воздушном потоке
Измельчение в воздушном потоке Техническое описание и анализ конструкции маслонасосов
Техническое описание и анализ конструкции маслонасосов Отражение света
Отражение света Инфракрасное, ультрафиолетовое и рентгеновское излучения
Инфракрасное, ультрафиолетовое и рентгеновское излучения