Содержание
- 2. I.Механика. Кинематика зависит от положения точки на траектории, характеризуемой расстоянием s от точки, принятой за начальную
- 3. I.Механика. Кинематика и для нормального ускорения , где - единичный вектор нормали. Окончательно получим . Первое
- 4. I.Механика. Кинематика За время одного оборота (период обращения T) и . Величину обратную Т называют частотой
- 5. I.Механика. Кинематика Обратное соотношение имеет вид Если направление оси вращения в пространстве не изменяется, то знаки
- 6. I.Механика. Кинематика Движение тела, брошенного под углом к горизонту Пусть тело брошено с поверхности земли со
- 7. I.Механика. Кинематика По оси у В высшей точке траектории скорость обращается в ноль, откуда время подъема
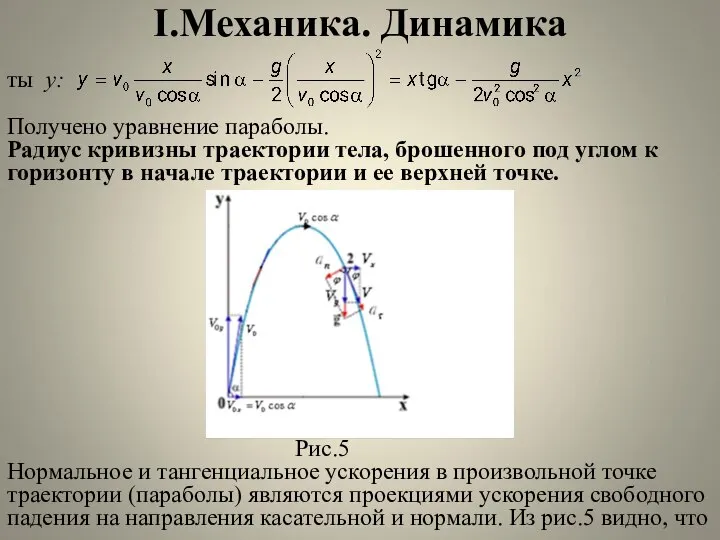
- 8. I.Механика. Динамика ты y: Получено уравнение параболы. Радиус кривизны траектории тела, брошенного под углом к горизонту
- 9. I.Механика. Кинемаика , где угол определяется из соотношения проекций cкорости R – радиус кривизны траектории. Наибольший
- 10. I.Механика. Кинематика Примеры решения задач Задача 1. Радиус-вектор материальной точки изменяется по закону см. Найдите модуль
- 11. I.Механика. Кинематика Задача 3. Ускорение материальной точки изменяется со временем по закону ax = 15t1/2 (м/с2).
- 12. I.Механика. Кинематика , где начальная скорость, g- ускорение свободного падения. Рис.6 Горизонтальная дальность полета равна ,
- 13. I.Механика. Кинематика Задача 5. Сколько оборотов совершит вращающееся тело за время от t1 = 3 c
- 15. Скачать презентацию











 Презентация по физике Опыт Иоффе
Презентация по физике Опыт Иоффе  Прогнозирование разовых замен деталей
Прогнозирование разовых замен деталей Источники света. Распространение света
Источники света. Распространение света Тепловые свойства и тепловой режим почв
Тепловые свойства и тепловой режим почв Теория решения изобретательских задач. Законы кинематики
Теория решения изобретательских задач. Законы кинематики Застосування магнітних матеріалів
Застосування магнітних матеріалів Адсорбация ПАВ на границе раствор - газ
Адсорбация ПАВ на границе раствор - газ Электроемкость. Конденсатор
Электроемкость. Конденсатор Моделирование работы газового хроматографа. Создание алгоритма для работы виртуальной модели прибора
Моделирование работы газового хроматографа. Создание алгоритма для работы виртуальной модели прибора Защитное зануление
Защитное зануление Наукові досягнення 20 ст
Наукові досягнення 20 ст Презентация по физике Теплопроводность
Презентация по физике Теплопроводность  Начальные этапы развития лучевого поражения
Начальные этапы развития лучевого поражения Физика минералов и их аналогов
Физика минералов и их аналогов Нерозгалужене коло з активним опором та індуктивністю
Нерозгалужене коло з активним опором та індуктивністю Динамика материальной точки
Динамика материальной точки Свойства воды
Свойства воды №37 01.02.2022
№37 01.02.2022 Кипение воды. Опыты
Кипение воды. Опыты Импульс тела. Закон сохранения импульса
Импульс тела. Закон сохранения импульса Внеклассное мероприятие по физике: Звездный час
Внеклассное мероприятие по физике: Звездный час Основы термодинамики
Основы термодинамики Динамические системы
Динамические системы Одноканальная аппаратура тонального телеграфирования. Тактико-технические данные и общее устройство аппаратуры. (Тема 8.1)
Одноканальная аппаратура тонального телеграфирования. Тактико-технические данные и общее устройство аппаратуры. (Тема 8.1) История создания швейной машины, их виды
История создания швейной машины, их виды Автор презентации – учитель МКОУ СОШ №11 г. Палласовки Волгоградской области Букешева Гулзара Нурболатовна
Автор презентации – учитель МКОУ СОШ №11 г. Палласовки Волгоградской области Букешева Гулзара Нурболатовна Радиациялық сәулелену
Радиациялық сәулелену Звёзды
Звёзды