Содержание
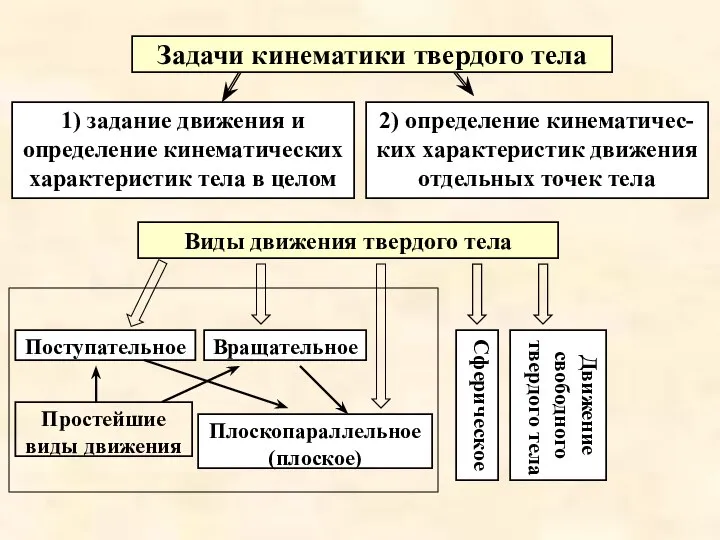
- 2. Задачи кинематики твердого тела 2) определение кинематичес-ких характеристик движения отдельных точек тела Вращательное Движение свободного твердого
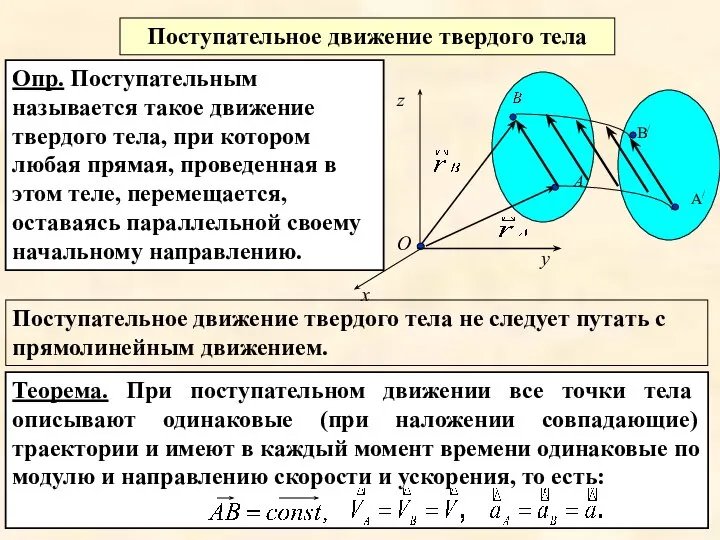
- 3. Теорема. При поступательном движении все точки тела описывают одинаковые (при наложении совпадающие) траектории и имеют в
- 4. При поступательном движении общую для всех точек тела скорость - ускорением поступательного движения тела. называют скоростью
- 5. Опр. Угол ϕ между полуплоскостями I и II, определяющий положение вращающегося тела, называется углом поворота. Угол
- 6. Угловую скорость можно изобразить в виде вектора и который направлен вдоль оси вращения тела в ту
- 7. Вывод. Угловое ускорение определяется по формуле (2) Угловое ускорение. Опр. Величина, характеризующая быстроту изменения угловой скорости
- 8. Если вращение ускоренное, то векторы Угловое ускорение можно изобразить в виде вектора направлены в одну сторону
- 9. Частные случаи вращения тела Равномерное вращение Опр. Вращение тела называется равномерным, если угловая скорость тела остается
- 10. Опр. Если величины ω и ε имеют одинаковые знаки, вращение будет равноускоренным, а если разные –
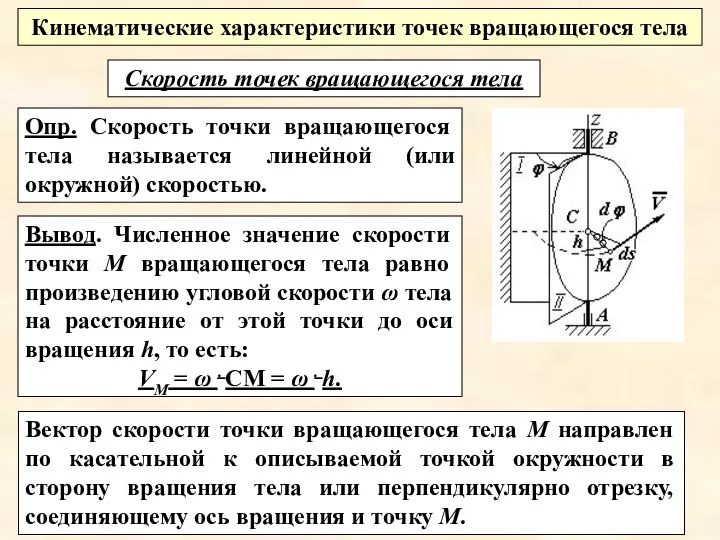
- 11. Вывод. Численное значение скорости точки М вращающегося тела равно произведению угловой скорости ω тела на расстояние
- 12. Вектор направлен по главной нормали, которая в случае вращательного движения будет направлена по радиусу окружности. Модуль
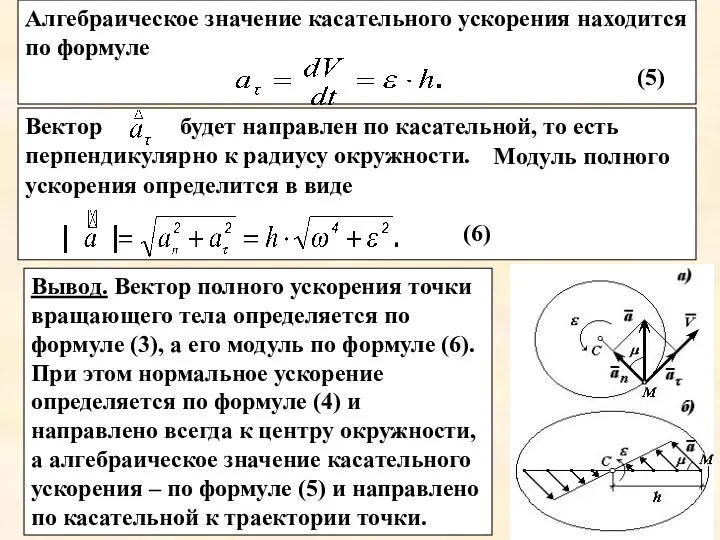
- 13. Вектор будет направлен по касательной, то есть перпендикулярно к радиусу окружности. Алгебраическое значение касательного ускорения находится
- 14. Вывод б). Вектор ускорения любой точки вращающегося тела равен геометрической сумме векторов составляющих ускорений Представление векторов
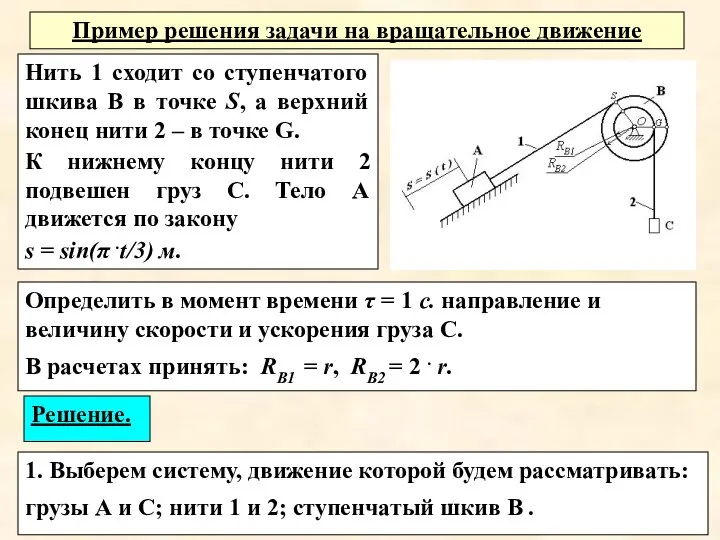
- 15. Определить в момент времени τ = 1 с. направление и величину скорости и ускорения груза С.
- 16. 2. Определим вид движения, в котором находится каждое тело системы: грузы А и С, нити 1
- 17. 4. Определим скорость и ускорение точки S шкива В. Так как нить 1 находится в поступательном
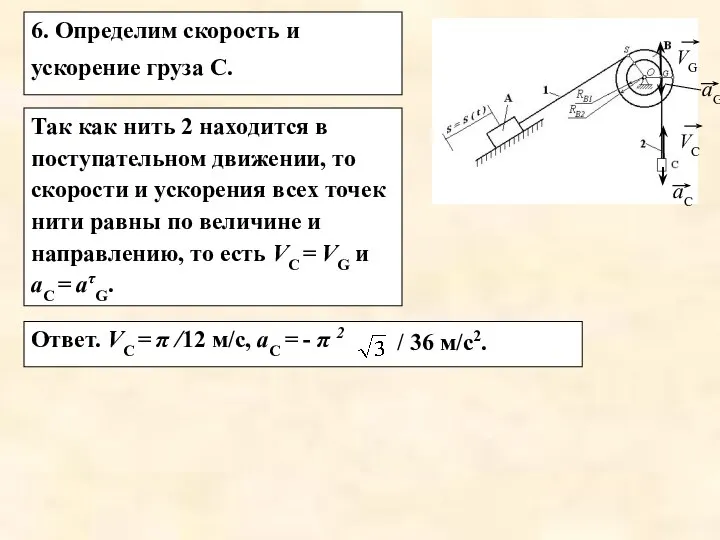
- 18. 6. Определим скорость и ускорение груза С. Так как нить 2 находится в поступательном движении, то
- 19. ЗАДАНИЕ № ДЕ 1- 7 Два шкива соединены ременной передачей. Точка А одного из шкивов имеет
- 21. Скачать презентацию












 Электроскоп. Опыты Франклина
Электроскоп. Опыты Франклина Двигатель внутреннего сгорания
Двигатель внутреннего сгорания Фотоэффект. Дискретное представление света
Фотоэффект. Дискретное представление света Три состояния вещества
Три состояния вещества Группа коленвала. Кривошипно-шатунный механизм
Группа коленвала. Кривошипно-шатунный механизм Модели атомов Опыт Резерфорда
Модели атомов Опыт Резерфорда Авторы: М.Ю. Фризен, учитель физики В.В. Широких, учитель литературы
Авторы: М.Ю. Фризен, учитель физики В.В. Широких, учитель литературы Архимед методологиясы және механикасы
Архимед методологиясы және механикасы Тема урока: Квартирная электропроводка 8 класс Раздел «ЭЛЕКТРОТЕХНИЧЕСКИЕ РАБОТЫ »
Тема урока: Квартирная электропроводка 8 класс Раздел «ЭЛЕКТРОТЕХНИЧЕСКИЕ РАБОТЫ » Характер философского знания и задачи философии
Характер философского знания и задачи философии Солнечная батарея
Солнечная батарея Криволинейное движение. Движение тела по окружности
Криволинейное движение. Движение тела по окружности Эйнштейн 1879-1955 «Хочу выяснить, каким фундаментальным законам следовал Бог, создавая Вселенную. Ничто иное меня не интересует.»
Эйнштейн 1879-1955 «Хочу выяснить, каким фундаментальным законам следовал Бог, создавая Вселенную. Ничто иное меня не интересует.» Теплотехника. Теплопроводность
Теплотехника. Теплопроводность Законы сохранения и изменения момента импульса в механике
Законы сохранения и изменения момента импульса в механике ІІ закон термодинаміки
ІІ закон термодинаміки  Коливання. Механічні коливання
Коливання. Механічні коливання 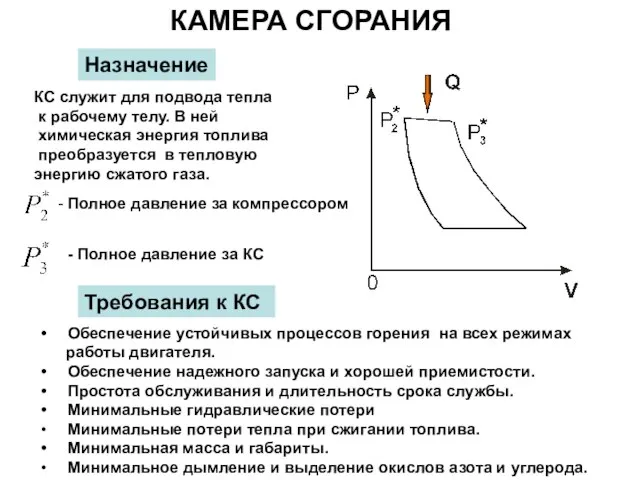 Камера сгорания. Назначение
Камера сгорания. Назначение Електричний струм у металах
Електричний струм у металах Презентация по физике Плазма Электрический ток в плазме
Презентация по физике Плазма Электрический ток в плазме  Сила трения. Трение покоя
Сила трения. Трение покоя Основные законы физики
Основные законы физики Современные проблемы физики наноструктурных материалов. Методы аттестации структуры наноматериалов
Современные проблемы физики наноструктурных материалов. Методы аттестации структуры наноматериалов История изобретения турбин
История изобретения турбин Вращающиеся тросовые космические системы
Вращающиеся тросовые космические системы Магнит. Магнит өріс бағыты
Магнит. Магнит өріс бағыты Презентация по физике "Зрительные иллюзии" - скачать бесплатно
Презентация по физике "Зрительные иллюзии" - скачать бесплатно Презентация по физике "Геометрическая оптика." - скачать
Презентация по физике "Геометрическая оптика." - скачать