Содержание
- 2. ВВЕДЕНИЕ Теория электромагнитного поля как раздел курса «Физические основы квантовой электроники». Основное внимание - электромагнитным волнам
- 3. Уравнения Максвелла в сплошной среде
- 4. Уравнения Максвелла, интегральная форма S – двумерная поверхность, замкнутая для теоремы Гаусса и открытая для законов
- 5. Справочные формулы В декартовых координатах В цилиндрических координатах
- 6. Справочные формулы В сферических координатах
- 7. Материальные уравнения Соотношения между D, B, E и H В вакууме D = E, B =
- 8. Упражнения (векторный анализ)
- 9. Упражнения Вывести из уравнений Максвелла закон Кулона для точечного заряда в вакууме. Проверить выполнение всех уравнений
- 10. Уравнение непрерывности Закон сохранения электрического заряда
- 11. «Площади» э.-м. поля Рассматриваем ограниченные в пространстве и времени пакеты поля (с конечной энергией) Интегрируем по
- 12. Уравнения Максвелла в вакууме (СГС) D = E, B = H, ρ = 0, j =
- 13. Квантовые ограничения в слабых полях Уравнения Максвелла отвечают континуальному (а не дискретному) описанию. Поэтому для их
- 14. Квантовые ограничения в сильных полях В уравнениях Максвелла не учитываются вероятность рождения электрон-позитронных пар и эффекты
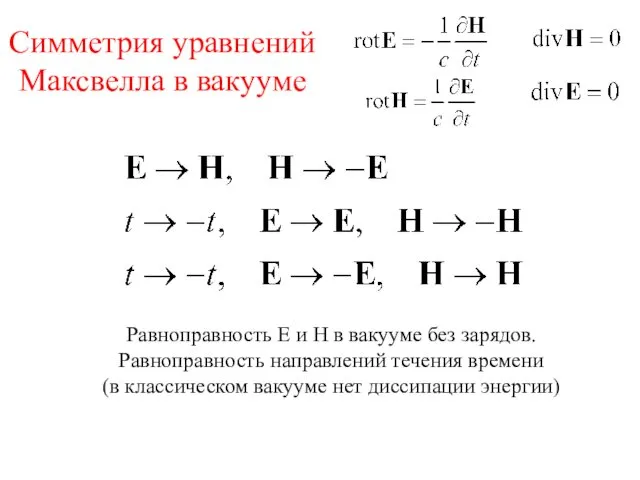
- 15. Симметрия уравнений Максвелла в вакууме Равноправность Е и Н в вакууме без зарядов. Равноправность направлений течения
- 16. Векторная структура уравнений Максвелла ρ – скаляр (плотность эл. заряда) E, D, j – полярные трехмерные
- 17. Волновое уравнение Немагнитные среды Не все решения волнового уравнения служат решениями уравнений Максвелла, поскольку эти решения
- 18. Динамика э.-м. поля При заданных материальных соотношениях возможна постановка задачи Коши – по начальным данным определяется
- 19. Динамика э.-м. поля в вакууме Уравнения Максвелла содержат производные по времени первого порядка. Поэтому задания напряженностей
- 20. Начальные условия (вакуум) не произвольны. Они должны подчиняться условиям Если это так, то и в последующие
- 21. Динамика поля (задача Коши)* Поскольку уравнения Максвелла – первого порядка по времени, то начальные условия позволяют
- 22. Динамика поля*
- 23. Динамика поля*
- 24. Задания
- 25. Эволюционная переменная, пример уравнения Гельмгольца Однородная среда (вакуум), монохроматическое излучение с частотой ω Фиксированная (линейная) поляризация.
- 26. Задача Коши для уравнения Гельмгольца Рассмотрим пучок монохроматического излучения с преимущественным направлением вдоль оси z Зададим
- 27. Задача Коши для уравнения Гельмгольца Предел При нулевых (в пределе) начальных данных есть решение, стремящееся при
- 28. Ковариантная формулировка уравнений Максвелла в вакууме. Тензоры электромагнитного поля Напряженности электрического и магнитного полей не абсолютны
- 29. Ковариантная формулировка …* Вводим 4-мерное пространство-время с координатами xk, k = 0, 1, 2, 3 Другая
- 30. 4-векторы Ковариантный 4-вектор (нижние индексы) Контравариантный 4-вектор (верхние индексы) Напряженности электрического и магнитного полей не составляют
- 31. 4-тензоры ковариантный (нижние индексы) контравариантный (верхние индексы)
- 32. Тензор электромагнитного поля Антисимметрия
- 33. Преобразование Лоренца напряженностей э.-м. поля (спец. случай)
- 34. Ковариантная форма уравнений Максвелла
- 35. Инварианты
- 36. Тензор энергии-импульса э.-м. поля Симметрия по индексам ? Символ Кронекера при i = k и 0
- 37. Задания Найти напряженности электрического и магнитного полей точечного заряда, движущегося с постоянной скоростью. Проверить инвариантность величин
- 38. Уравнение распространения фронта электромагнитной волны Ранее мы решали задачу Коши, то есть по начальным данным (при
- 39. Законы сохранения для э.-м. поля в вакууме Уч. пособие, стр. 17-20
- 40. Потенциалы поля и волновое уравнение Уч. пособие, стр. 20-22
- 42. Скачать презентацию






































 История развития физики. Физика и техника
История развития физики. Физика и техника Метод минимизации энергии. Основы классической молекулярной динамики
Метод минимизации энергии. Основы классической молекулярной динамики Плавление тел
Плавление тел  Покорение вершины знаний
Покорение вершины знаний Аттестационная работа. Физический практикум в 11 классе с использованием лабораторного оборудования
Аттестационная работа. Физический практикум в 11 классе с использованием лабораторного оборудования Ганс Гейгер и Генрих Мюллер. Счетчик Гейгера
Ганс Гейгер и Генрих Мюллер. Счетчик Гейгера Тепловое движение(игра)
Тепловое движение(игра) Феноменологическая термодинамика Энтропия и ее статистический смысл. Критическая изотерма. Эффект Джоуля-Томсона. (Лекция 12)
Феноменологическая термодинамика Энтропия и ее статистический смысл. Критическая изотерма. Эффект Джоуля-Томсона. (Лекция 12) Свойства атмосферы и земной поверхности, влияющие на распространение радиоволн
Свойства атмосферы и земной поверхности, влияющие на распространение радиоволн Перемещение тела при равноускоренном движении
Перемещение тела при равноускоренном движении Давление насыщенных паров
Давление насыщенных паров Радиоактивность. Альфа-, бета-, гамма- распад атомного ядра
Радиоактивность. Альфа-, бета-, гамма- распад атомного ядра Физика. Вводная лекция
Физика. Вводная лекция Вычисление электрических полей и потенциалов с помощью теоремы Остроградского-Гаусса
Вычисление электрических полей и потенциалов с помощью теоремы Остроградского-Гаусса Работа газа и пара при расширении. Двигатель внутреннего сгорания
Работа газа и пара при расширении. Двигатель внутреннего сгорания Комплексные методы анализа ГХ-МС и ВЭЖХ-МС
Комплексные методы анализа ГХ-МС и ВЭЖХ-МС Технологические требования к конструкции сварных и паяных соединений
Технологические требования к конструкции сварных и паяных соединений Теплотехника. Подобие процессов конвективного теплообмена. (Лекция 13)
Теплотехника. Подобие процессов конвективного теплообмена. (Лекция 13) Презентация по физике "Законы Ньютона. Инерциальные системы отсчёта" - скачать
Презентация по физике "Законы Ньютона. Инерциальные системы отсчёта" - скачать  Оптические иллюзии
Оптические иллюзии Презентация по физике Дифракция света
Презентация по физике Дифракция света  Импульс, закон сохранения импульса
Импульс, закон сохранения импульса Неравномерное движение. Мгновенная скорость
Неравномерное движение. Мгновенная скорость Ядролық гамма-резонанс
Ядролық гамма-резонанс Оптика. Геометрическая оптика
Оптика. Геометрическая оптика Денелердің өзара әрекеттесуі. Дененің массасы «Заттың тығыздығы»
Денелердің өзара әрекеттесуі. Дененің массасы «Заттың тығыздығы» Тепловые двигатели
Тепловые двигатели Колебания кристаллической решетки
Колебания кристаллической решетки