Содержание
- 2. Модель атома. В центре атома неподвижный точечный заряд (ядро), создающий вокруг себя стационарное электростатическое поле. В
- 3. В результате возмущения электрон перескакивает на возбужденный уровень. Возбужденное состояние электрона неустойчиво. Через некоторое время электрон
- 4. Одномерное уравнение Шредингера для водородоподобного атома. Квантование энергии Выберем систему координат, начало которой совмещено с центром
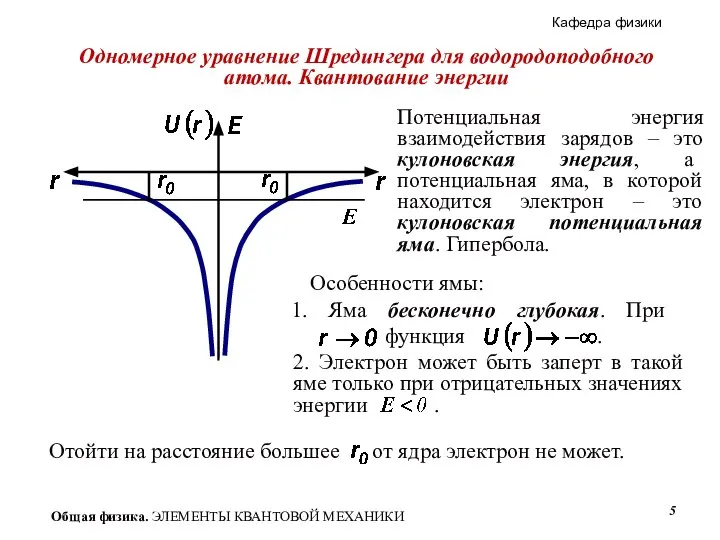
- 5. Одномерное уравнение Шредингера для водородоподобного атома. Квантование энергии Особенности ямы: Потенциальная энергия взаимодействия зарядов – это
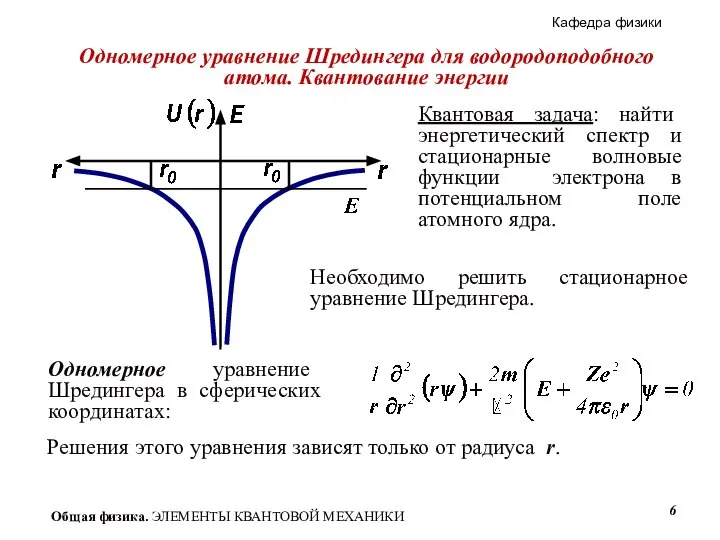
- 6. Квантовая задача: найти энергетический спектр и стационарные волновые функции электрона в потенциальном поле атомного ядра. Необходимо
- 7. Из теории дифференциальных уравнений: решения, удовлетворяющие условиям однозначности, конечности и непрерывности волновой функции, получаются только при
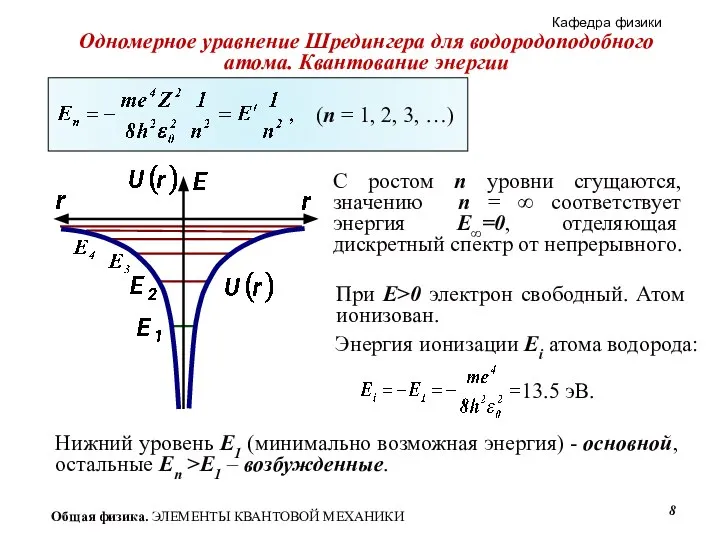
- 8. С ростом n уровни сгущаются, значению n = ∞ соответствует энергия E∞=0, отделяющая дискретный спектр от
- 9. Общая физика. АТОМ ВОДОРОДА В КВАНТОВОЙ ФИЗИКЕ Общее решение уравнения Шредингера для водородоподобного атома. Квантовые числа.
- 10. Общая физика. АТОМ ВОДОРОДА В КВАНТОВОЙ ФИЗИКЕ Общее решение уравнения Шредингера для водородоподобного атома. Квантовые числа.
- 11. Общая физика. АТОМ ВОДОРОДА В КВАНТОВОЙ ФИЗИКЕ Общее решение уравнения Шредингера для водородоподобного атома. Квантовые числа.
- 12. Общая физика. АТОМ ВОДОРОДА В КВАНТОВОЙ ФИЗИКЕ Общее решение уравнения Шредингера для водородоподобного атома. Квантовые числа.
- 13. Общая физика. АТОМ ВОДОРОДА В КВАНТОВОЙ ФИЗИКЕ Общее решение уравнения Шредингера для водородоподобного атома. Квантовые числа.
- 14. Общая физика. АТОМ ВОДОРОДА В КВАНТОВОЙ ФИЗИКЕ Общее решение уравнения Шредингера для водородоподобного атома. Квантовые числа.
- 15. Общая физика. АТОМ ВОДОРОДА В КВАНТОВОЙ ФИЗИКЕ Классификация стационарных состояний электрона в водородоподобном атоме. Следовательно, можно
- 17. Скачать презентацию











 Механические волны. Звук. (Лекция 2)
Механические волны. Звук. (Лекция 2) Настройка трансмиссии
Настройка трансмиссии Электротехника және электроника. Трансформаторлар
Электротехника және электроника. Трансформаторлар Імітаційна модель виміру параметрів сигналів частотної маніпуляції
Імітаційна модель виміру параметрів сигналів частотної маніпуляції ФИЗИКА 7 класс «Сложение двух сил, направленных по одной прямой Равнодействующая сил»
ФИЗИКА 7 класс «Сложение двух сил, направленных по одной прямой Равнодействующая сил» Биологическое действие искусственных электромагнитных излучений
Биологическое действие искусственных электромагнитных излучений Гидравлика. Относительный покой жидкости
Гидравлика. Относительный покой жидкости Процессы формирования водородной плазмы в зоне резания
Процессы формирования водородной плазмы в зоне резания Электромагнитные Электромагнитные волны Выполнил: Рис Филипп
Электромагнитные Электромагнитные волны Выполнил: Рис Филипп Электр зарядының сақталу заңы
Электр зарядының сақталу заңы Газовые законы. Идеальный газ и уравнение его состояния. Модель идеального газа
Газовые законы. Идеальный газ и уравнение его состояния. Модель идеального газа Судоремонтные предприятия
Судоремонтные предприятия Элементы специальной теории относительности. Релятивистская динамика
Элементы специальной теории относительности. Релятивистская динамика Линейные цепи постоянного тока
Линейные цепи постоянного тока Radar ambiguity function
Radar ambiguity function Презентация по физике Резонансная частота
Презентация по физике Резонансная частота  Плоская произвольная система сил
Плоская произвольная система сил Физический эксперимент в основной школе
Физический эксперимент в основной школе  Встановлення приводів і техніка безпеки при їх обслуговуванні
Встановлення приводів і техніка безпеки при їх обслуговуванні Термоэлектрические материалы. Предмет, задачи и области применения термоэлектриков
Термоэлектрические материалы. Предмет, задачи и области применения термоэлектриков Изобретение радио А.С. Поповым 1
Изобретение радио А.С. Поповым 1 Звуковые волны
Звуковые волны Закон преломления света. Решение задач на закон преломления света
Закон преломления света. Решение задач на закон преломления света Прибор для измерения давления - манометр
Прибор для измерения давления - манометр Отрицательное влияние тепловых машин на окружающую среду связано с действием различных факторов. Отрицательное влияние теп
Отрицательное влияние тепловых машин на окружающую среду связано с действием различных факторов. Отрицательное влияние теп Построение плана ускорений кривошипно-ползунных механизмов. (Лекция 4)
Построение плана ускорений кривошипно-ползунных механизмов. (Лекция 4) Устройство микроскопа
Устройство микроскопа Место реакции Белоусова-Жаботинского в науке
Место реакции Белоусова-Жаботинского в науке