Содержание
- 2. Квантовая статистика Рассмотрим систему из двух тождественных частиц. Координаты одной ξ1, другой ξ2 ⇒ Функция ψ(ξ1,ξ2),
- 3. Частицы с полуцелым спином (электроны, нуклоны) описываются антисимметричными ψ – функциями, находятся в квантовых состояниях поодиночке
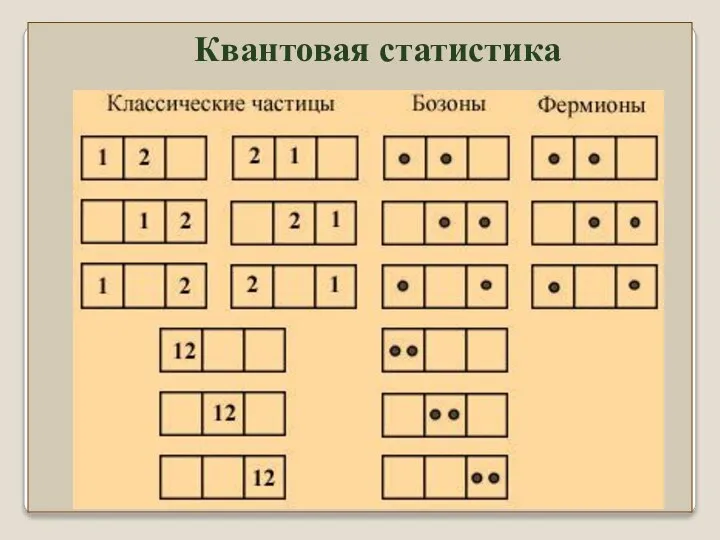
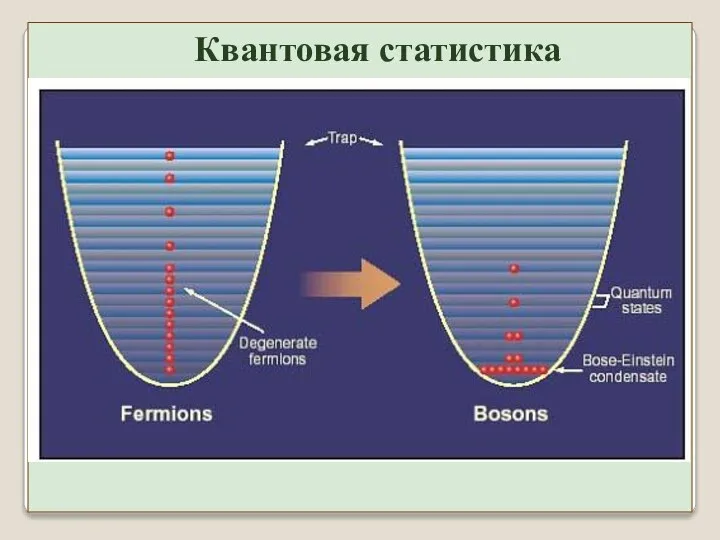
- 4. Фермионы и бозоны при размещении по ячейкам ведут себя по-разному. Фермионы согласно принципу Паули. Для бозонов
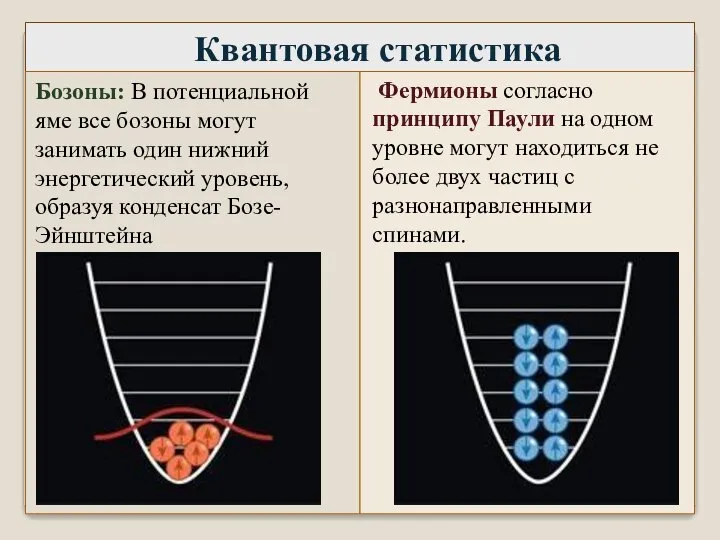
- 5. Квантовая статистика Бозоны: В потенциальной яме все бозоны могут занимать один нижний энергетический уровень, образуя конденсат
- 6. Одной из основных задач статистической физики является нахождение закона распределения частиц по разным квантовым состояниям. Рассматривается
- 7. Фазовое пространство Фазовое пространство – шестимерное пространство с взаимно-перпендикулярными осями: x, y, z, px, py, pz
- 8. Квантовая статистика
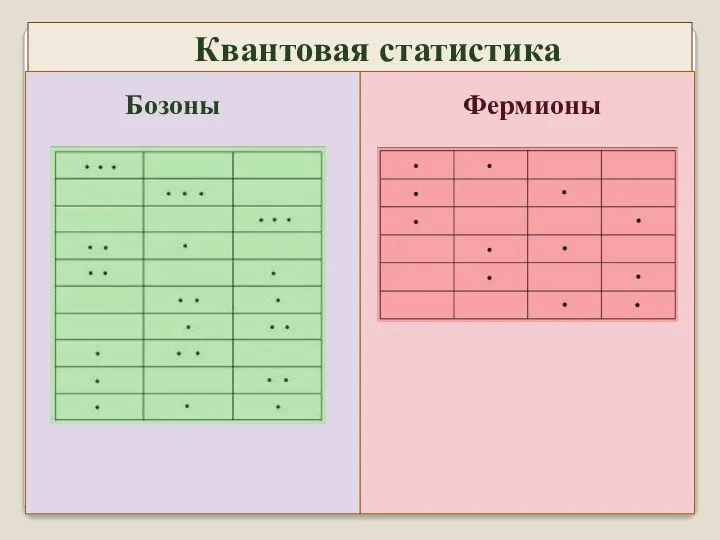
- 9. Бозоны Фермионы Квантовая статистика
- 10. Для фермионов считаем все возможные перестановки ячеек (пустых и занятых) ⇒ Z!, перестановки местами частиц N!
- 11. Энергия частицы ε зависит от координат и импульса ε = f(x, y, z, px, py, pz).
- 12. Статистический вес системы равен произведению Надо найти наиболее вероятное распределение частиц по ячейкам, т.е. найти максимум
- 13. После сложных математических преобразований (формула Стирлинга, множители Лагранжа) получаются формулы: Для фермионов: Для бозонов: Квантовая статистика
- 14. Распределение Ферми- Дирака Распределение Бозе – Эйнштейна. Отличаются только знаком в знаменателе. Квантовая статистика
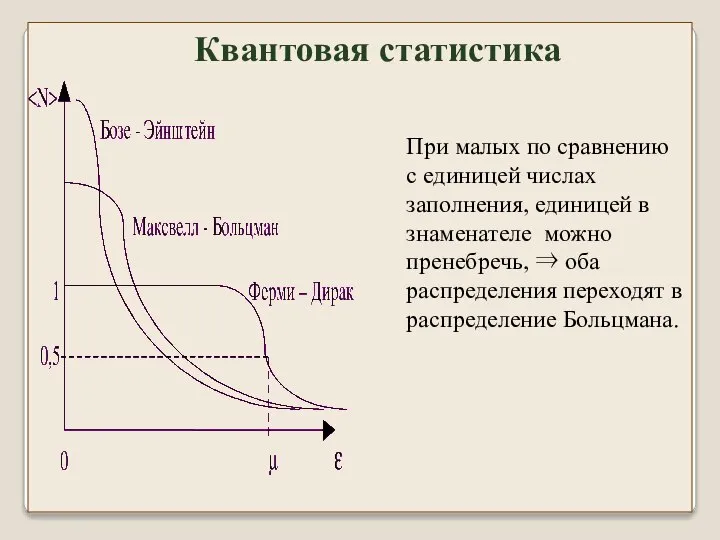
- 15. Квантовая статистика При малых по сравнению с единицей числах заполнения, единицей в знаменателе можно пренебречь, ⇒
- 16. Параметр распределения μ называется химическим потенциалом. Является функцией температуры, определяется, как и энергия частицы, с точностью
- 17. Квантовая статистика
- 18. Фотонный газ и формула Планка При обычных (не лазерных) интенсивностях световые волны не возмущают друг друга.
- 19. Число ячеек Zi в этом слое определяется как 2∙ΔVμ / h3, т.к. в каждой ячейке два
- 20. Учитывая ⇒ и ΔEi = Zi· ·ħωi ⇒ Фотонный газ и формула Планка Совпадает с формулой
- 21. Фононный газ и формула Дебая Аналогично, колебания кристаллической решетки можно представить как фононный газ.
- 22. Хотя фононы – квазичастицы, они подчиняются той же статистике и к ним применяется распределение Бозе –
- 23. Плотность энергии Для упругих волн в кристалле: Фононный газ и формула Дебая
- 24. Распределение Ферми-Дирака
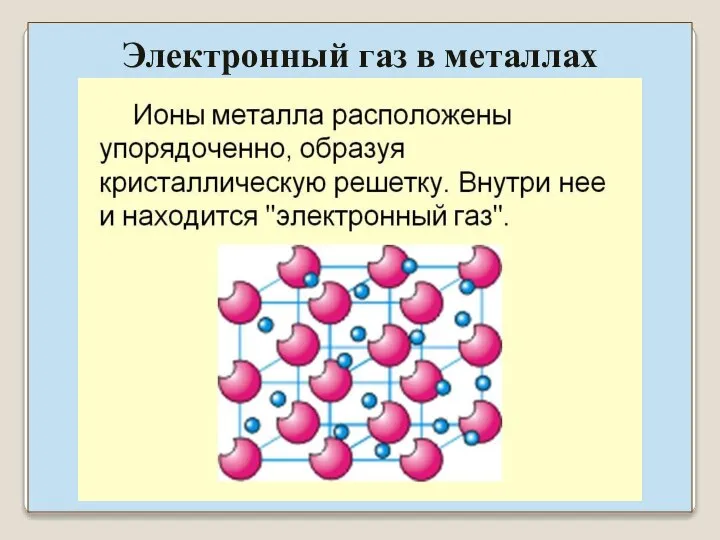
- 25. Электронный газ в металлах
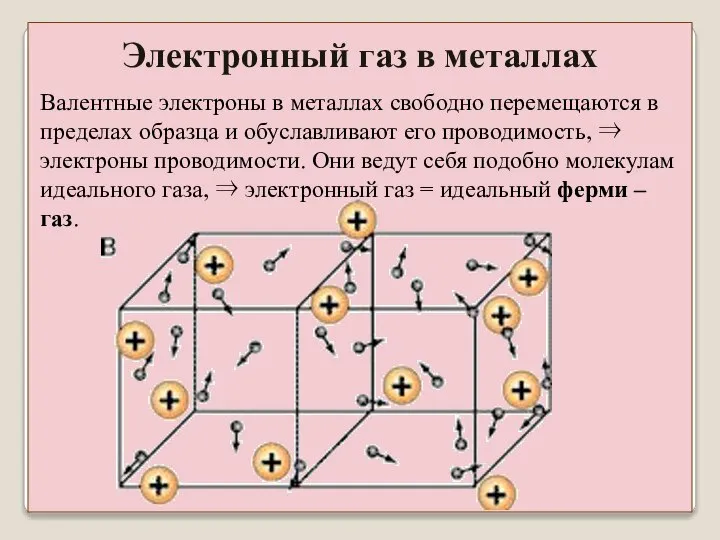
- 26. Валентные электроны в металлах свободно перемещаются в пределах образца и обуславливают его проводимость, ⇒ электроны проводимости.
- 27. Электроны распределяются по энергетическим уровням в соответствии с функцией Ферми – Дирака. Электроны обладают одной и
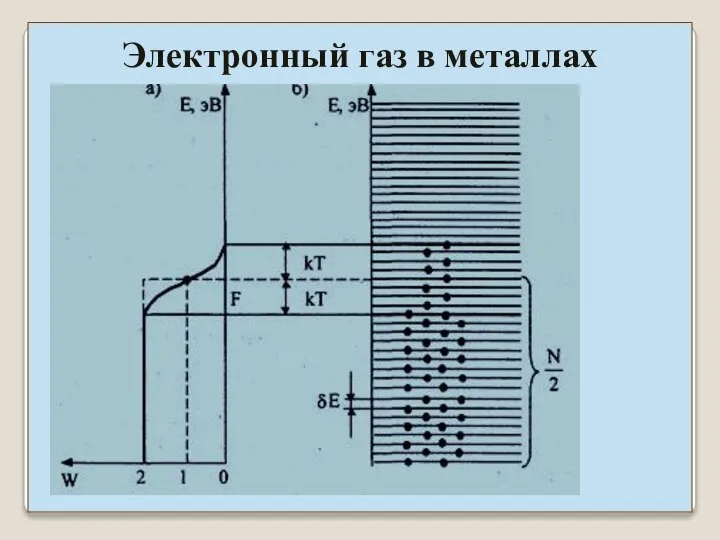
- 28. При абсолютном нуле электроны располагаются попарно на самых низких уровнях: = 2 если εi = 0
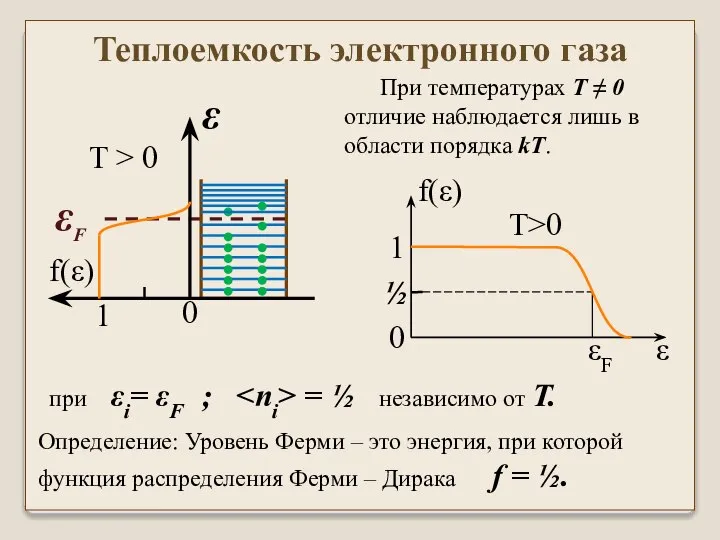
- 29. При температурах T ≠ 0 отличие наблюдается лишь в области порядка kT. Определение: Уровень Ферми –
- 30. Электронный газ в металлах
- 31. Для свободных электронов U = 0 ⇒ В случае свободных электронов изоэнергетическая поверхность εi= εF в
- 32. Т.к. каждой ячейке соответствуют два состояния с разными спинами, ⇒ где число состояний Электронный газ в
- 33. при T = 0 заполнены N нижних состояний N = nV, где n – концентрация свободных
- 34. Средняя энергия электронов при абсолютном нуле: ⇒ = 3 эВ, соответствует 2.5∙104 К Уровень ферми слабо
- 35. Электронный газ в металлах
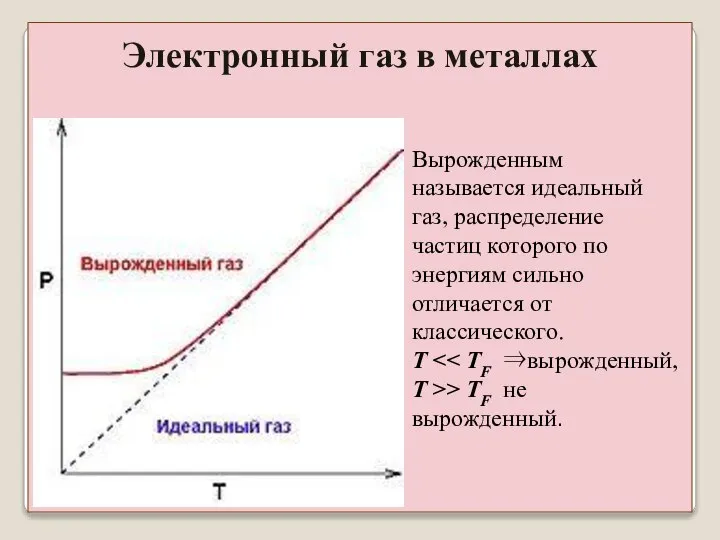
- 36. Вырожденным называется идеальный газ, распределение частиц которого по энергиям сильно отличается от классического. T T >>
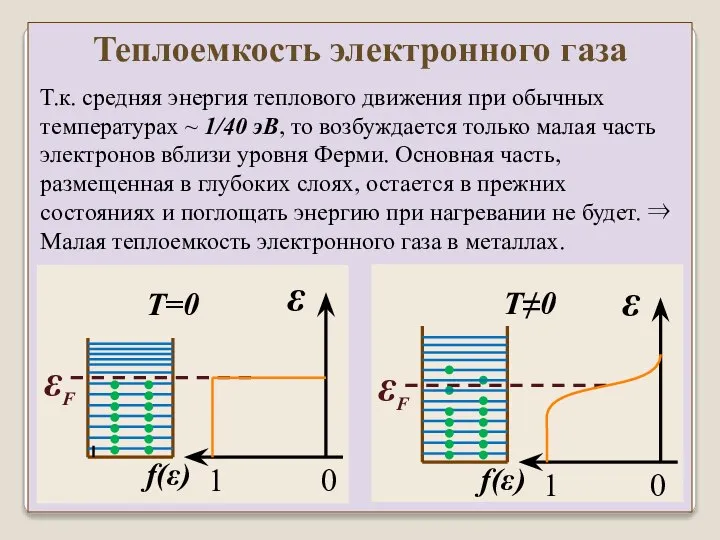
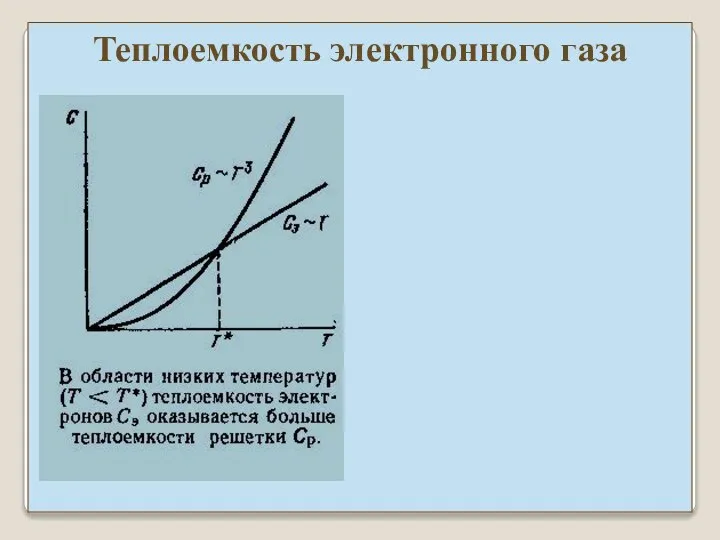
- 37. Теплоемкость электронного газа Т.к. средняя энергия теплового движения при обычных температурах ~ 1/40 эВ, то возбуждается
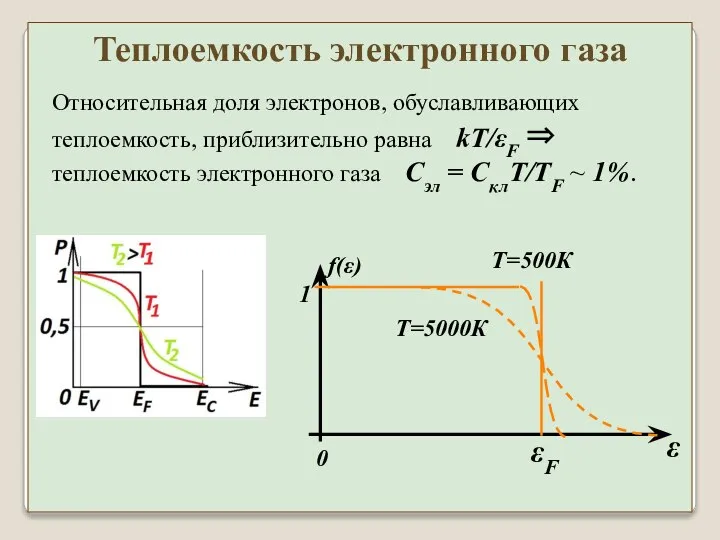
- 38. Относительная доля электронов, обуславливающих теплоемкость, приблизительно равна kT/εF ⇒ теплоемкость электронного газа Cэл = CклT/TF ~
- 39. Теплоемкость электронного газа
- 41. Скачать презентацию

























 Первый закон термодинамики. Необратимость процессов в природе
Первый закон термодинамики. Необратимость процессов в природе Подготовил ученик 11 класса МОУ «Сош п.Сланцевый Рудник» Матросов Дима
Подготовил ученик 11 класса МОУ «Сош п.Сланцевый Рудник» Матросов Дима Експериментальна перевірка властивостей електромагнітних хвиль
Експериментальна перевірка властивостей електромагнітних хвиль Изучение микроструктуры процессов релаксации в плазме
Изучение микроструктуры процессов релаксации в плазме Эксперимент по физике высоких энергий
Эксперимент по физике высоких энергий Презентация Архимедова сила
Презентация Архимедова сила  Разработка комплексной автоматизации мобильного узла подачи газа
Разработка комплексной автоматизации мобильного узла подачи газа Презентация по физике Теплопроводность
Презентация по физике Теплопроводность  Как устроен атом
Как устроен атом Квантовые постулаты Бора Нильса
Квантовые постулаты Бора Нильса Электрические источники света
Электрические источники света Бета-распад
Бета-распад Отрицательное влияние тепловых машин на окружающую среду связано с действием различных факторов. Отрицательное влияние теп
Отрицательное влияние тепловых машин на окружающую среду связано с действием различных факторов. Отрицательное влияние теп Техническое обслуживание и текущий ремонт ходовой части
Техническое обслуживание и текущий ремонт ходовой части Люминесцентные лампы
Люминесцентные лампы Волны Эллиотта
Волны Эллиотта Электрическая прочность диэлектриков
Электрическая прочность диэлектриков Затухающие и вынужденные колебания (лекция 6)
Затухающие и вынужденные колебания (лекция 6) Зубчатая передача электровоза ВЛ11
Зубчатая передача электровоза ВЛ11 Биотехнология и генетическая инженерия
Биотехнология и генетическая инженерия  Охлаждение, нагревание тел конечных размеров. Нагрев параллелепипеда
Охлаждение, нагревание тел конечных размеров. Нагрев параллелепипеда Исследование зависимости силы тока в проводнике от напряжения на его концах. Лабораторная работа
Исследование зависимости силы тока в проводнике от напряжения на его концах. Лабораторная работа Учитель физики МОУ «СОШ с. Агафоновка Питерского района Саратовской области» Дзюрич Елена Алексеевна
Учитель физики МОУ «СОШ с. Агафоновка Питерского района Саратовской области» Дзюрич Елена Алексеевна  Теплота сгорания топлива
Теплота сгорания топлива ВПР. Трен и флэт. ХМА и ХТ. Лекция 5
ВПР. Трен и флэт. ХМА и ХТ. Лекция 5 Интерференция света
Интерференция света Развитие средств связи
Развитие средств связи Сила трения
Сила трения