Содержание
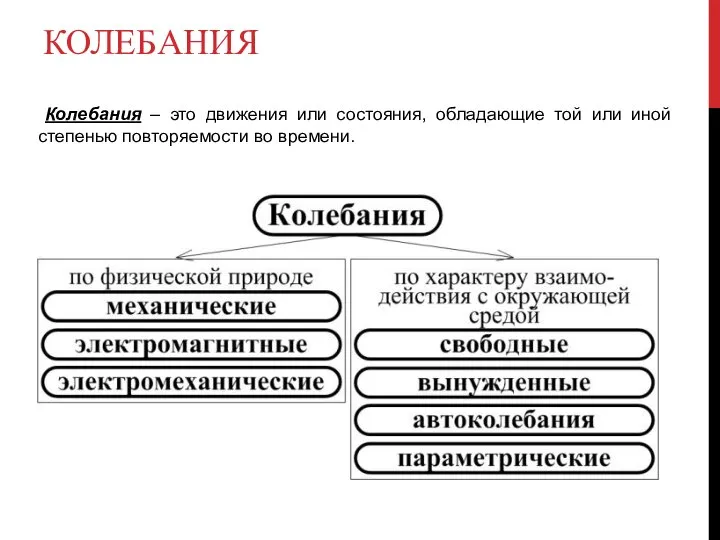
- 2. КОЛЕБАНИЯ Колебания – это движения или состояния, обладающие той или иной степенью повторяемости во времени.
- 3. КОЛЕБАНИЯ Следует отметить, что среди всевозможных периодических наибольшее значение имеют гармонические колебания. Это связано с тем,
- 4. КОЛЕБАНИЯ Свободные колебания Свободные колебания – это колебания, совершающиеся при отсутствии внешнего воздействия за счёт первоначально
- 5. КОЛЕБАНИЯ Отсюда следует уравнение Решением уравнения будет , где Здесь x – смещение тела от положения
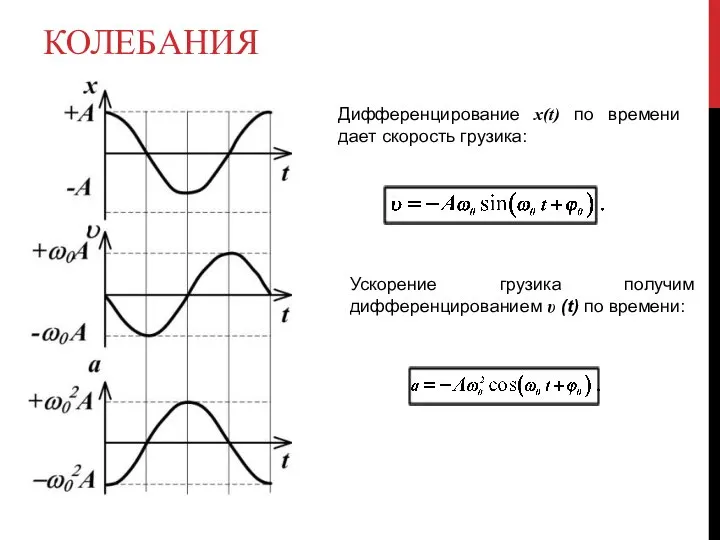
- 6. КОЛЕБАНИЯ Дифференцирование x(t) по времени дает скорость грузика: Ускорение грузика получим дифференцированием υ (t) по времени:
- 7. КОЛЕБАНИЯ Гармонические колебания могут совершаться не только в связи с упругой силой, но и благодаря другим
- 8. КОЛЕБАНИЯ
- 9. КОЛЕБАНИЯ Затухающие колебания Когда гармонические свободные колебания совершаются в реальной среде, на колебательную систему действуют силы
- 10. КОЛЕБАНИЯ
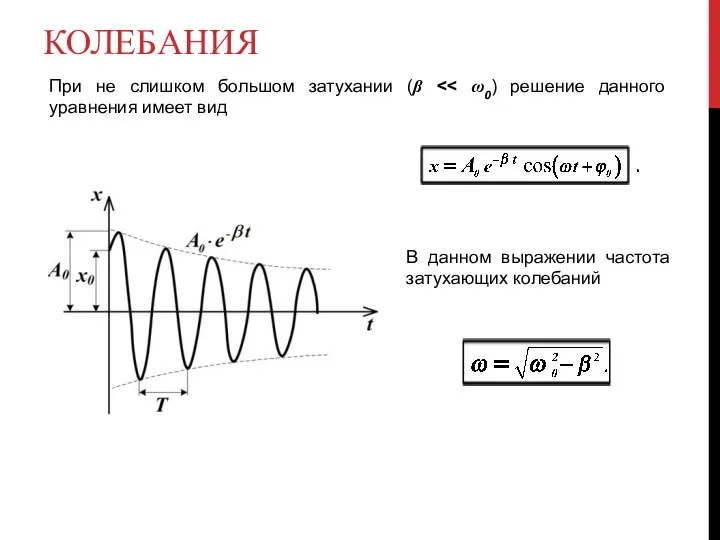
- 11. КОЛЕБАНИЯ При не слишком большом затухании (β В данном выражении частота затухающих колебаний
- 12. КОЛЕБАНИЯ Коэффициент затухания – это величина, характеризующая скорость затухания колебаний и обратная времени, в течении которого
- 13. КОЛЕБАНИЯ Вынужденные колебания Вынужденные колебания – это колебания, которые совершаются колебательной системой, подвергающейся воздействию внешней периодической
- 14. КОЛЕБАНИЯ Решение данного уравнения
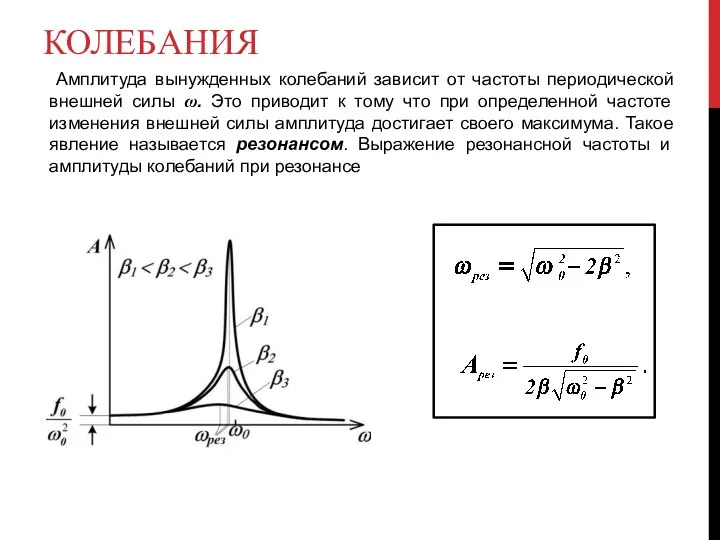
- 15. КОЛЕБАНИЯ Амплитуда вынужденных колебаний зависит от частоты периодической внешней силы ω. Это приводит к тому что
- 16. КОЛЕБАНИЯ
- 17. КОЛЕБАНИЯ Маятники Пружинный маятник – это колебательная система, состоящая из пружины с коэффициентом жесткости k, соединенной
- 18. КОЛЕБАНИЯ Математический маятник – это тело небольших размеров, подвешенное на тонкой нерастяжимой нити, и совершающее колебания
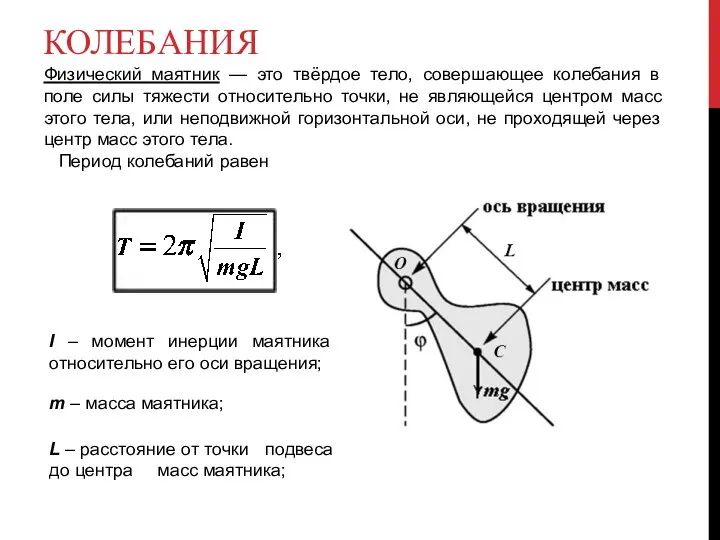
- 19. КОЛЕБАНИЯ Физический маятник — это твёрдое тело, совершающее колебания в поле силы тяжести относительно точки, не
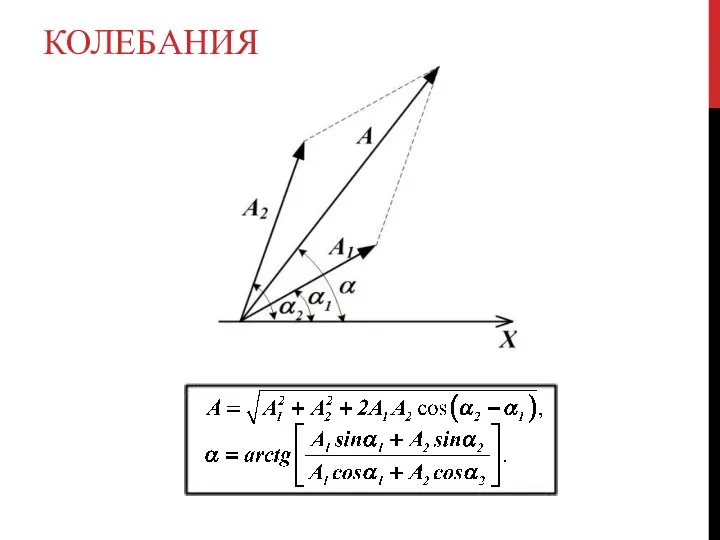
- 20. КОЛЕБАНИЯ Векторная диаграмма. Сложение колебаний одного направления Гармоническое колебание может быть представлено в виде вектора, отложенного
- 21. КОЛЕБАНИЯ
- 23. ВОЛНЫ Волна – это процесс распространения колебаний в среде. Если внешняя сила, приложенная к элементарному объему
- 24. ВОЛНЫ
- 25. ВОЛНЫ Уравнение бегущей волны Пусть источник гармонических колебаний находится в т. О, лежащей на оси X.
- 26. ВОЛНЫ Данное выражение, записанное в виде называется уравнением бегущей волны (плоской). В данном выражении ξ (x
- 27. ВОЛНЫ Волновое уравнение Напомним, что уравнение гармонического колебания является решением дифференциального уравнения колебаний (свободных, затухающих, вынужденных).
- 28. ВОЛНЫ Скорость распространения упругих волн Скорость распространения продольных волн определяется выражением , где E – модуль
- 29. ВОЛНЫ Модуль сдвига равен отношению касательного напряжения к величине угла сдвига G = τ / γ
- 30. ВОЛНЫ Энергия упругой волны Распространение волны в упругой среде сопровождается передачей энергии. При этом не происходит
- 31. ВОЛНЫ Вспомним, что потенциальная энергия растянутой пружины определяется как (kx2)/2. Учитывая аналогию между коэффициентом жесткости пружины
- 33. Скачать презентацию






















 Сила тяжести, вес тела
Сила тяжести, вес тела Масса өтудің модифицирленген теңдеуі
Масса өтудің модифицирленген теңдеуі Презентация по физике "радиоактивность" - скачать
Презентация по физике "радиоактивность" - скачать  Линейные антенные решетки
Линейные антенные решетки Вопросы к экзамену по высшей геодезии
Вопросы к экзамену по высшей геодезии Проводники. Конденсаторы. Электроемкость
Проводники. Конденсаторы. Электроемкость Охлаждение. Смесительные теплообменники
Охлаждение. Смесительные теплообменники Электронные компоненты
Электронные компоненты Общие сведения о передачах
Общие сведения о передачах Режущий аппарат жатки зерноуборочного комбайна
Режущий аппарат жатки зерноуборочного комбайна Разделы физики, механики
Разделы физики, механики Магнитное поле в вакууме
Магнитное поле в вакууме Магнитные свойства вещества
Магнитные свойства вещества Көрсеткіштік және логарифмдік теңдеулерді шешу әдістері
Көрсеткіштік және логарифмдік теңдеулерді шешу әдістері Вимушене запалювання горючих систем (лекція 7)
Вимушене запалювання горючих систем (лекція 7) Урок по физике в 9 классе Подготовил учитель физики МОУ лицея №5 Терехова Наталья Николаевна 2008г.
Урок по физике в 9 классе Подготовил учитель физики МОУ лицея №5 Терехова Наталья Николаевна 2008г. Магнетизм. ЭМ колебания и волны
Магнетизм. ЭМ колебания и волны Скорость прямолинейного равноускоренного движения. График скорости
Скорость прямолинейного равноускоренного движения. График скорости Греет ли шуба? Автор: Черкасов Андрей, ученик 5 класса МАОУ «Лицей» г.Тобольска. Научный руководитель: Маликова Лали Джамбу
Греет ли шуба? Автор: Черкасов Андрей, ученик 5 класса МАОУ «Лицей» г.Тобольска. Научный руководитель: Маликова Лали Джамбу "Работа и мощность электрического тока
"Работа и мощность электрического тока Оператор автоматических и полуавтоматических линий, станков и установок
Оператор автоматических и полуавтоматических линий, станков и установок Аттестационная работа. Физика вокруг нас
Аттестационная работа. Физика вокруг нас Расчет силовой установки речного судна
Расчет силовой установки речного судна Изменение агрегатных состояний вещества (8 класс)
Изменение агрегатных состояний вещества (8 класс) Моделирование электрофизических свойств gaas методом монте-карло
Моделирование электрофизических свойств gaas методом монте-карло Синусоидалы ток тізбектері. Синусоидалы ток және оны сипаттайтын параметрлер
Синусоидалы ток тізбектері. Синусоидалы ток және оны сипаттайтын параметрлер Термомеханические испытания. Экспериментальная механика
Термомеханические испытания. Экспериментальная механика Изучение деления ядра атома урана по фотографиям треков
Изучение деления ядра атома урана по фотографиям треков