Содержание
- 2. Количеством движения материальной точки называется векторная величина, равная произведению массы точки на ее скорость Элементарным импульсом
- 3. Импульс силы за некоторый промежуток времени равен определенному интегралу от элементарного импульса, взятого по этому промежутку
- 4. § 1. Теорема об изменении количества движения точки (в дифференциальной форме) Производная по времени от количества
- 5. Теорема об изменении количества движения точки (в интегральной форме) Изменение количества движения точки за некоторый промежуток
- 6. Если задача пространственная (1-я задача динамики) Зная, как изменяется скорость точки, определить импульс действующих сил (2-я
- 7. § 2. Теорема моментов Моментом количества движения точки относительно некоторого центра О называется векторная величина, равная
- 8. Продифференцируем момент количества движения по времени или Теорема моментов относительно центра Производная по времени от момента
- 9. Основное уравнение динамики умножим слева векторно на радиус-вектор или
- 10. Спроектируем обе части равенства на ось Z, получим Теорема моментов относительно оси Производная по времени от
- 11. Если то Момент количества движения точки относительно некоторого центра есть величина постоянная, если момент действующей на
- 12. Пример. Рассмотрим движение материальной точки под действием центральной силы из (¤) =>
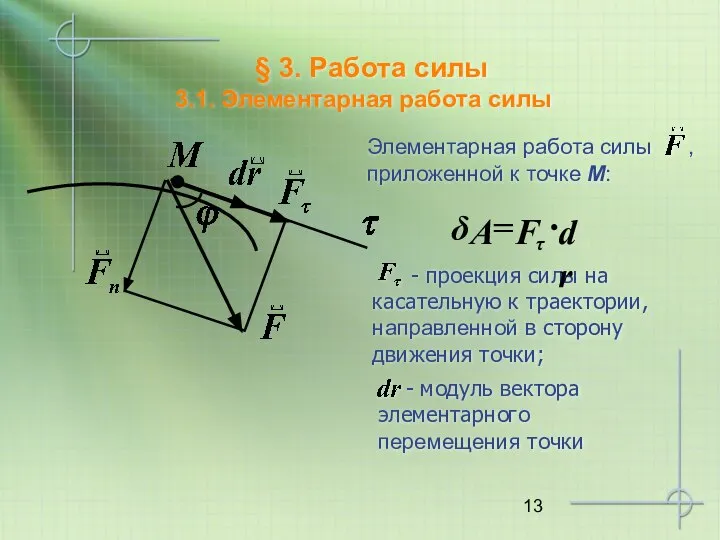
- 13. § 3. Работа силы 3.1. Элементарная работа силы
- 14. δA > 0, если Fτ > 0 Поскольку Fτ = m·aτ = m dV/dt , то
- 15. тогда ( * ) – аналитическое выражение элементарной работы Размерность: [A] = [H·м] = [Дж]
- 16. 3.2. Работа силы на конечном перемещении Работа силы на конечном перемещении есть предел суммы элементарных работ
- 17. 3.3. Примеры вычисления работы силы а) Работа постоянной силы на конечном перемещении (1)
- 18. Пример
- 19. б) Работа силы тяжести Воспользуемся (1) и вычислим работу силы тяжести на перемещении AB: или
- 20. в) Работа линейной силы упругости
- 21. § 4. Теорема об изменении кинетической энергии материальной точки , тогда Дифференциал кинетической энергии материальной точки
- 22. Кинетической энергией материальной точки называется скалярная величина, равная половине произведения массы точки на квадрат ее скорости
- 23. Интегрируем (5): Изменение кинетической энергии материальной точки на некотором ее перемещении равно сумме работ сил, действующих
- 24. § 5 Несвободное движение точки (Принцип Даламбера) Уравнения движения или условия равновесия можно получить, положив в
- 25. Жа́н Леро́н Д’Аламбе́р (фр. Jean Le Rond d'Alembert; 16 ноября 1717 — 29 октября 1783) французский
- 26. 5.1. Принцип Даламбера - векторную величину, равную по модулю ma и направленную в противоположную сторону ускорения,
- 27. - уравнение принципа Даламбера Если движущуюся точку в некоторый момент времени остановить, приложив к ней силу
- 28. Можно применять и для системы материальных точек, только необходимо помнить, что никакие реальные силы инерции на
- 29. 5.2. Относительное движение точки Основной закон динамики, общие теоремы и уравнение принципа Даламбера выполняются только в
- 30. Все уравнения и теоремы механики для относительного движения точки составляются так же, как уравнения абсолютного движения,
- 32. Скачать презентацию












![тогда ( * ) – аналитическое выражение элементарной работы Размерность: [A] = [H·м] = [Дж]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1478135/slide-14.jpg)















 Тема урока: «Давление газа»
Тема урока: «Давление газа» Формула Ляме
Формула Ляме Моделирование обтекания вертолёта при взлёте и посадке
Моделирование обтекания вертолёта при взлёте и посадке Автоматические регуляторы
Автоматические регуляторы НАНОТИХНОЛОГИИ В НАШЕЙ ЖИЗНИ Выполнил: Ученик 11В класса ГОУ БИЮЛИ Омаханов Мурад Наставник: к.ф.-м.н. Андреева Наталья Владими
НАНОТИХНОЛОГИИ В НАШЕЙ ЖИЗНИ Выполнил: Ученик 11В класса ГОУ БИЮЛИ Омаханов Мурад Наставник: к.ф.-м.н. Андреева Наталья Владими Электротехника и электроника. Однофазные электрические цепи синусоидального тока. (Лекция 2)
Электротехника и электроника. Однофазные электрические цепи синусоидального тока. (Лекция 2) Взаємодія тіл. Сила
Взаємодія тіл. Сила Колесо с резиновыми спицами
Колесо с резиновыми спицами Резонанс в линейных электрических цепях
Резонанс в линейных электрических цепях Решение задач. (Лекция 4)
Решение задач. (Лекция 4) Электролиз. История создания. Применение
Электролиз. История создания. Применение Презентация по физике "Ультрафіолетові випромінювання" - скачать бесплатно
Презентация по физике "Ультрафіолетові випромінювання" - скачать бесплатно Основні способи отримання низьких та наднизьких температур
Основні способи отримання низьких та наднизьких температур Экономия электроэнергии
Экономия электроэнергии Статика. Равновесие тел
Статика. Равновесие тел Технологические процессы и производства. Преобразование энергии на ТЭС
Технологические процессы и производства. Преобразование энергии на ТЭС Необходимость и методы уравновешивания двс. (лекция 11)
Необходимость и методы уравновешивания двс. (лекция 11) Презентация по физике "Закон Шарля" - скачать
Презентация по физике "Закон Шарля" - скачать  Электромагнитное поле 9 класс Учитель физики МОУ «СОШ с. Рефлектор» Леснова Н.П.
Электромагнитное поле 9 класс Учитель физики МОУ «СОШ с. Рефлектор» Леснова Н.П. Турбина, первичный двигатель с вращательным движением рабочего органа
Турбина, первичный двигатель с вращательным движением рабочего органа Астероиды. Основная информация
Астероиды. Основная информация Задача № 1 на расчет плотности тела
Задача № 1 на расчет плотности тела Приспособления к швейной машине
Приспособления к швейной машине Линза и глаз
Линза и глаз Электродинамика 2013. Тест 2
Электродинамика 2013. Тест 2 Лекция 3. Электромагнитная индукция
Лекция 3. Электромагнитная индукция Исследовательская работа на тему: «Влияние магнитных полей на живые организмы». Работа по физике Учениц 9 «Б» класса Лицея им.
Исследовательская работа на тему: «Влияние магнитных полей на живые организмы». Работа по физике Учениц 9 «Б» класса Лицея им.  Конструкция беспилотного летательного аппарата
Конструкция беспилотного летательного аппарата