Содержание
- 2. Независимость угловой скорости и углового ускорения плоской фигуры от выбора полюса – Выберем два произвольных прямолинейных
- 3. Мгновенный центр скоростей (МЦС) – При движении плоской фигуры в каждый момент времени существует точка, жестко
- 4. Примеры использования МЦС для определения скоростей точек плоской фигуры – Поскольку при движении плоской фигуры в
- 5. Примеры использования МЦС для определения скоростей точек плоской фигуры 5 Дано: vA, vB, vA║vB, положения точек
- 6. Мгновенный центр ускорений (МЦУ) – При движении плоской фигуры в каждый момент времени существует точка, жестко
- 8. Скачать презентацию
Независимость угловой скорости и углового ускорения плоской фигуры от выбора полюса
Независимость угловой скорости и углового ускорения плоской фигуры от выбора полюса
Углы наклона отрезков к горизонтальной оси различны и связаны между собой соотношением:
Продифференцируем это соотношение:
Отсюда следует, что угловые скорости двух отрезков равны:
После повторного дифференцирования следует,
что угловые ускорения двух отрезков также равны:
Таким образом, угловая скорость и угловое ускорение
плоской фигуры не зависят от выбора полюса и их можно представить в виде векторов, перпендикулярных плоскости фигуры:
Теорема о сложении скоростей – Скорость любой точки плоской фигуры равна геометрической сумме скоростей полюса и вращательной скорости этой точки вокруг полюса.
Радиусы-векторы точек A и B связаны между собой соотношением:
Продифференцируем это соотношение:
Второе слагаемое есть вращательная
скорость точки B вокруг полюса A:
Таким образом, скорость точки B равна геометрической сумме скорости полюса A и вращательной скорости точки B вокруг полюса :
Следствие 1 – Проекции скоростей точек плоской фигуры на ось,
проходящую через эти точки равны .
x1
Спроецируем векторное соотношение на ось x1:
Следствие 2 – Концы векторов скоростей точек плоской фигуры, лежащих на одной прямой, также
лежат на одной прямой и делят эту прямую на отрезки пропорциональные расстояниям между точками.
Концы векторов вращательных скоростей точек B и A лежат на одной прямой и делят ее на отрезки
пропорциональные расстояниям между точками:
Концы векторов скоростей полюса A лежат, изображенных
в точках B и C также лежат на одной прямой.
11
Мгновенный центр скоростей (МЦС) – При движении плоской фигуры в каждый
Мгновенный центр скоростей (МЦС) – При движении плоской фигуры в каждый
Пусть известна скорость одной из точек фигуры и угловая скорость вокруг этой точки:
Запишем векторное соотношение для скорости некоторой точки P согласно теоремы о сложении скоростей:
Зададим значение скорости этой точки P равной нулю:
Тогда получаем:
Это позволяет найти положение МЦС (точки P), а именно: МЦС должен находиться на перпендикуляре к скорости точки A, отложенном в сторону угловой скорости, на расстоянии:
Т.е. вращательная скорость искомой точки должна быть равна по модулю скорости точки A, параллельна этой скорости и направлена в противоположную сторону.
Если положение МЦС найдено, скорость любой точки плоской фигуры может быть легко определена посредством выбора полюса в МСЦ . В этом случае векторное выражение теоремы о сложении скоростей вырождается в известную зависимость скорости от расстояния до центра вращения:
Другими словами, можно утверждать, что в любой момент времени тело
не совершает никакого другого движения,
кроме как вращательного движения вокруг МЦС.
12
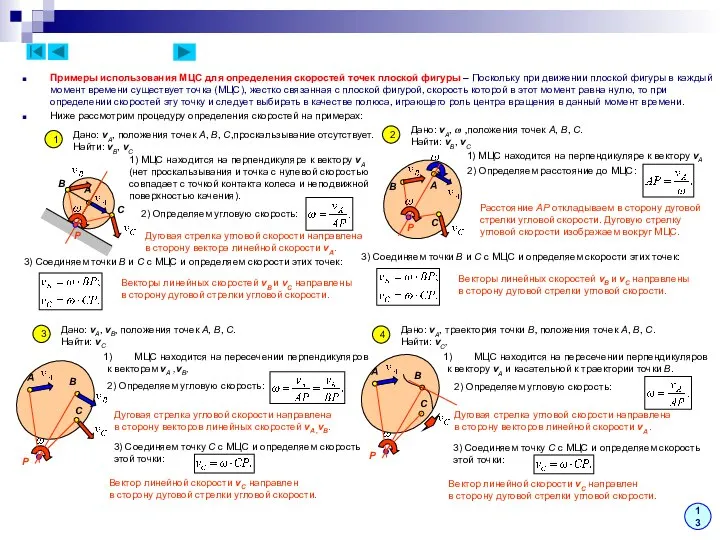
Примеры использования МЦС для определения скоростей точек плоской фигуры – Поскольку
Примеры использования МЦС для определения скоростей точек плоской фигуры – Поскольку
Ниже рассмотрим процедуру определения скоростей на примерах:
1
Дано: vA, положения точек A, B, C,проскальзывание отсутствует.
Найти: vB, vC
1) МЦС находится на перпендикуляре к вектору vA
(нет проскальзывания и точка с нулевой скоростью
совпадает с точкой контакта колеса и неподвижной
поверхностью качения).
2) Определяем угловую скорость:
3) Соединяем точки B и C с МЦС и определяем скорости этих точек:
Дуговая стрелка угловой скорости направлена
в сторону вектора линейной скорости vA.
Векторы линейных скоростей vB и vC направлены
в сторону дуговой стрелки угловой скорости.
2
Дано: vA, ω ,положения точек A, B, C.
Найти: vB, vC
1) МЦС находится на перпендикуляре к вектору vA
2) Определяем расстояние до МЦС:
3) Соединяем точки B и C с МЦС и определяем скорости этих точек:
Расстояние AP откладываем в сторону дуговой
стрелки угловой скорости. Дуговую стрелку
угловой скорости изображаем вокруг МЦС.
Векторы линейных скоростей vB и vC направлены
в сторону дуговой стрелки угловой скорости.
3
Дано: vA, vB, положения точек A, B, C.
Найти: vC
МЦС находится на пересечении перпендикуляров
к векторам vA ,vB,
2) Определяем угловую скорость:
Вектор линейной скорости vC направлен
в сторону дуговой стрелки угловой скорости.
Дуговая стрелка угловой скорости направлена
в сторону векторов линейных скоростей vA ,vB.
3) Соединяем точку C с МЦС и определяем скорость
этой точки:
4
Дано: vA, траектория точки B, положения точек A, B, C.
Найти: vC,
МЦС находится на пересечении перпендикуляров
к вектору vA и касательной к траектории точки B.
2) Определяем угловую скорость:
Вектор линейной скорости vC направлен
в сторону дуговой стрелки угловой скорости.
Дуговая стрелка угловой скорости направлена
в сторону векторов линейной скорости vA .
3) Соединяем точку C с МЦС и определяем скорость
этой точки:
13
Примеры использования МЦС для определения скоростей точек плоской фигуры
5
Дано: vA, vB,
Примеры использования МЦС для определения скоростей точек плоской фигуры
5
Дано: vA, vB,
Найти: vC
1) МЦС находится на пересечении перпендикуляров
к векторам vA и vB. Эта точка находится в бесконечности.
2) Угловая скорость обращается в нуль (мгновенно
поступательное движение):
3) Скорость точки C равна геометрически скоростям точек
A и B:
Вектор скорости точки C направлен параллельно векторам скоростей точек A и B (в ту же сторону).
6
Дано: vA, vB, vA║vB, положения точек A, B, C.
Найти: vC
1) МЦС находится на пересечении перпендикуляров
к векторам vA и vB. Эти перпендикуляры сливаются
в одну линию.
2) Определяем положение МЦС
(проводим линию через концы
векторов vA и vB) и угловую
скорость:
3) Соединяем точку C с МЦС и определяем скорость этой точки:
Дуговую стрелку угловой скорости изображаем
в сторону векторов линейных скоростей vA ,vB.
Вектор линейной скорости vC направлен
в сторону дуговой стрелки угловой скорости.
7
Дано: vA, vB, vA║vB, положения точек A, B, C.
Найти: vC
1) МЦС находится на пересечении перпендикуляров
к векторам vA и vB. Эти перпендикуляры сливаются
в одну линию.
2) Определяем положение МЦС
(проводим линию через концы
векторов vA и vB) и угловую
скорость:
3) Соединяем точку C с МЦС и определяем скорость этой точки:
Дуговую стрелку угловой скорости изображаем
в сторону векторов линейных скоростей vA ,vB.
Вектор линейной скорости vC направлен
в сторону дуговой стрелки угловой скорости.
Пример использования МЦС при исследовании работы
кривошипно-шатунного механизма – См. решение задачи М.16.28
“Теоретическая механика в примерах и задачах. Кинематика” (электронное
пособие автора www.miit.ru/institut/ipss/faculties/trm/main.htm ),
Теорема о сложении ускорений – Ускорение любой точки
плоской фигуры равна геометрической сумме ускорения полюса
и ускорения этой точки вокруг полюса.
Скорости точек A и B связаны между собой соотношением:
Продифференцируем это соотношение по времени:
Второе слагаемое дифференцируем как произведение двух функций:
Получили сумму вращательного и осестремительного ускорений
рассматриваемой точки относительно полюса. Таким образом,
ускорение точки плоской фигуры:
Следствие – Концы векторов ускорений точек плоской
фигуры, лежащих на одной прямой, также лежат на одной
прямой и делят ее на отрезки, пропорциональные расстояниям
между точками.
Концы векторов ускорений точек aBA и aСA
лежат на одной прямой Abc и делят ее на
отрезки пропорциональные расстояниям
между точками:
Концы векторов ускорений полюса A,
изображенных в точках B и C, лежат
также лежат на одной прямой.
Нетрудно доказать из подобия треугольников, что концы векторов
суммарных ускорений точек B и C также лежат на одной прямой,
и делят эту прямую на части, пропорциональные расстояниям
между точками.
14
Мгновенный центр ускорений (МЦУ) – При движении плоской фигуры в каждый
Мгновенный центр ускорений (МЦУ) – При движении плоской фигуры в каждый
Пусть известно ускорение одной из точек фигуры, угловая скорость и угловое ускорение вокруг этой точки:
Запишем векторное соотношение для ускорения некоторой точки Q согласно теоремы о сложении ускорений:
Зададим значение ускорения этой точки Q равной нулю:
Тогда получаем:
Это позволяет найти положение МЦУ (точки Q), а именно: МЦУ должен находиться прямой, составляющей угол β к вектору ускорения точки A, проведенной в сторону углового ускорения, на расстоянии:
Т.е. ускорение искомой точки при вращении вокруг полюса должно быть равно по модулю ускорению точки A, параллельно этому ускорению и направлено в противоположную сторону.
Если положение МЦУ найдено, ускорение любой точки плоской фигуры может быть легко определено посредством выбора полюса в МСУ . В этом случае векторное выражение теоремы о сложении ускорений вырождается в известную зависимость полного ускорения от расстояния до центра вращения:
Таким образом, при определении ускорений точек плоской фигуры в данный момент времени
можно считать, что тело совершает вращательное движение вокруг МЦУ.
Внимание: На самом деле в данный момент тело вращается вокруг МЦС,
положение которого в общем случае не совпадает с положением МЦУ.
Угол между вектором полного ускорения точки
при вращении относительно центра равен:
Примеры использования МЦУ для определения ускорений точек плоской фигуры
1
Дано: aA, ε, ω, положения точек A, B.
Найти: aB
1) МЦУ находится на прямой , составляющей угол β
к вектору ускорения точки A, проведенной в сторону
углового ускорения, на расстоянии:
2) Соединяем точку B с МЦУ
и определяем ускорение этой точки:
15




 Перемещение при прямолинейном равноускоренном движении
Перемещение при прямолинейном равноускоренном движении Тест по теме Электромагнетизм
Тест по теме Электромагнетизм Таинственная энергетика пирамид. Работу выполнила ученица 10 А класса МОУ « СОШ № 95 им. Н. Щукина п. Архара» Остапенко
Таинственная энергетика пирамид. Работу выполнила ученица 10 А класса МОУ « СОШ № 95 им. Н. Щукина п. Архара» Остапенко  Lego 9689 Простые механизмы
Lego 9689 Простые механизмы Разработка технологии ремонта гильз цилиндров дизельных двигателей
Разработка технологии ремонта гильз цилиндров дизельных двигателей Измерение массы тела на рычажных весах
Измерение массы тела на рычажных весах Відкриття атомного ядра
Відкриття атомного ядра Источники света. Распространение света
Источники света. Распространение света Источники света. Прямолинейное распространение света.
Источники света. Прямолинейное распространение света. Кіріспе. Сенімділік теория түсініктемесі және басты анықтамасы. Техникалық жүйенің көрсеткіштері
Кіріспе. Сенімділік теория түсініктемесі және басты анықтамасы. Техникалық жүйенің көрсеткіштері Устройство увеличительных приборов и правила работы с ними
Устройство увеличительных приборов и правила работы с ними Определение шума и вибрации
Определение шума и вибрации Нетрадиционные электростанции
Нетрадиционные электростанции Использование солнечной энергии на Земле
Использование солнечной энергии на Земле Голография
Голография Электрический ток в различных средах. Закономерность протекания тока
Электрический ток в различных средах. Закономерность протекания тока Квантовые явления. Ядро атома
Квантовые явления. Ядро атома Энергияның негізгі көздері, электрстанцияларының сипаттамасы
Энергияның негізгі көздері, электрстанцияларының сипаттамасы Метрики. Эффективность распараллеливания. (Лабораторная работа 2)
Метрики. Эффективность распараллеливания. (Лабораторная работа 2) Источники света. Распространение света
Источники света. Распространение света ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ. ВНУТРЕННЯЯ ЭНЕРГИЯ. РАБОТА И ТЕПЛОТА 1. Внутренняя энергия. Работа и теплота 2. Теплоёмкость идеал
ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ. ВНУТРЕННЯЯ ЭНЕРГИЯ. РАБОТА И ТЕПЛОТА 1. Внутренняя энергия. Работа и теплота 2. Теплоёмкость идеал Вынужленные колебания, затухающие колебания
Вынужленные колебания, затухающие колебания Презентация Давление. Гидравлический пресс
Презентация Давление. Гидравлический пресс  Закон сохранения импульса
Закон сохранения импульса Презентация по физике Тепловые явления Выполнила: ученица 8 «А» класса ГОУ СОШ №1973 Прохорчик Светлана
Презентация по физике Тепловые явления Выполнила: ученица 8 «А» класса ГОУ СОШ №1973 Прохорчик Светлана Силы в природе
Силы в природе  Биомеханические характеристики
Биомеханические характеристики Давление в технике и строительстве
Давление в технике и строительстве