Содержание
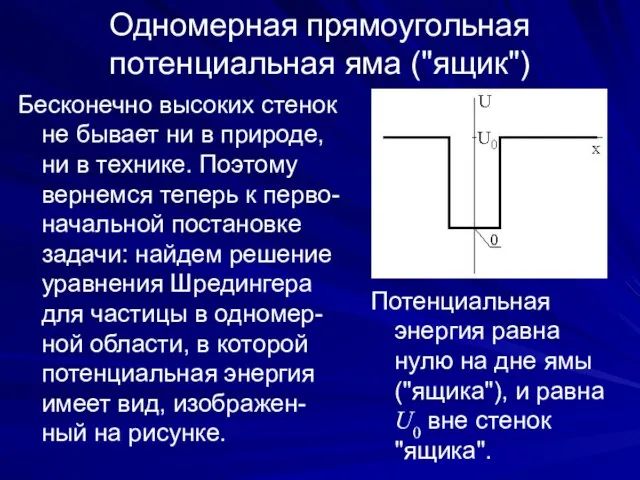
- 2. Одномерная прямоугольная потенциальная яма ("ящик") Бесконечно высоких стенок не бывает ни в природе, ни в технике.
- 3. Докажем прежде всего одно важное свойство собст-венных функций: собственные функции, принадле-жащие различным собственным значениям, орто-гональны, т.е.,
- 4. Если m = n, то интеграл не равен 0, и из ус-ловия нормировки можно найти коэф-фициент
- 5. Для поля, изображенного на рисун-ке, все пространство можно разделить на 3 области I, II, III: (10.9)
- 6. Подставляя в уравнение Шредингера усло-вие (10.9), получаем для областей I и III одинаковые уравнения: (10.10) а
- 7. Тогда уравнение (10.10) принимает вид: (10.12) а уравнение (10.11): (10.13) Для области II общее решение уравнения
- 8. Учтем условие, согласно которому волновая функ-ция не должна обращаться в бесконечность (усло-вие ограниченности). Слева от ямы
- 9. Итак, мы получили решения уравнения Шредингера для каждой из трех областей. Теперь эти решения надо "сшить"
- 10. Таким образом, получены 4 уравнения относитель-но 4 неизвестных A, B, C, D. Решить эту систему можно
- 11. Получили систему из 2-х однородных линейных уравнений для двух неизвестных A и B. Условием существования нетривиального
- 12. Подставляя первый корень (10.21) в уравнение (10.19), получаем: A = 0. Далее, из уравнений (10.15) -
- 13. Итак, волновые функции для 1-го корня имеют вид (10.25) где константа C определяется формулой (10.24). От-метим,
- 14. Из условия нормировки получаем формулу для константы C, совпадающую с формулой (10.24). Таким образом, волновые функции
- 15. Теперь надо сделать самое главное: определить спектр уровней энергии частицы в потенциальной яме. Для этого надо
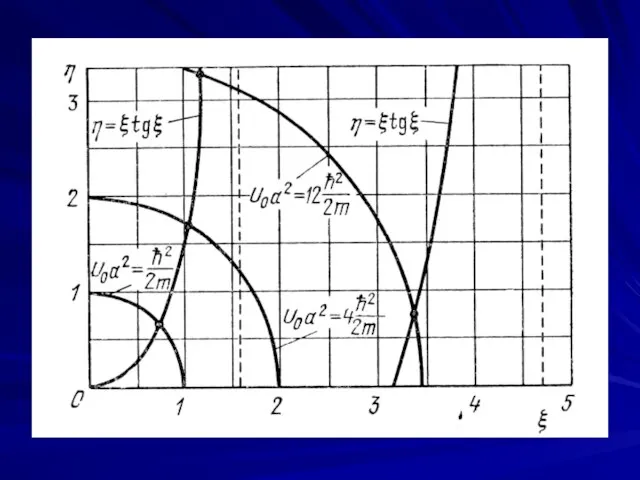
- 16. В "докомпьютерные" времена такие уравнения ре-шали графически следующим образом. Обозна-чим: Умножая обе части уравнения (10.21) на
- 17. Это уравнение окружности в координатах ξ и η с радиусом Искомые уровни энергии мож- но определить,
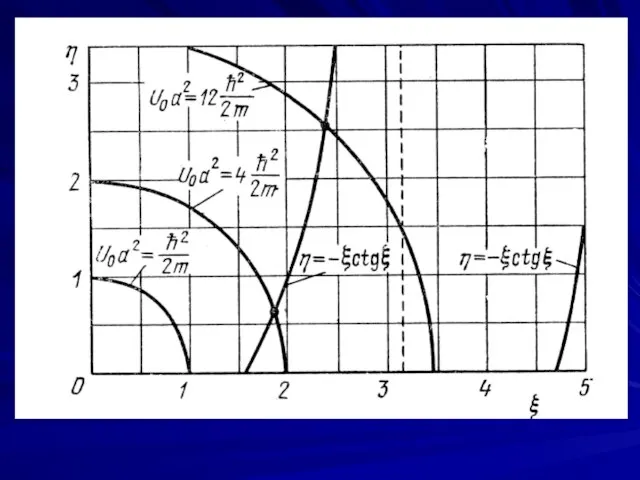
- 19. Выполняя аналогичные прео- бразования для формулы (10.22), получим Соответствующие значения энергии получим, найдя точки пересечения этой
- 21. В настоящее время подобные уравнения решают численными методами, причем решения получают за долю секунды и с
- 22. В пределе при U0 → полученные результаты должны совпадать с формулами, найденными выше для ямы с
- 24. Скачать презентацию


















 Представление вторичного квантования (фермионы)
Представление вторичного квантования (фермионы) Бензиновые двигатели
Бензиновые двигатели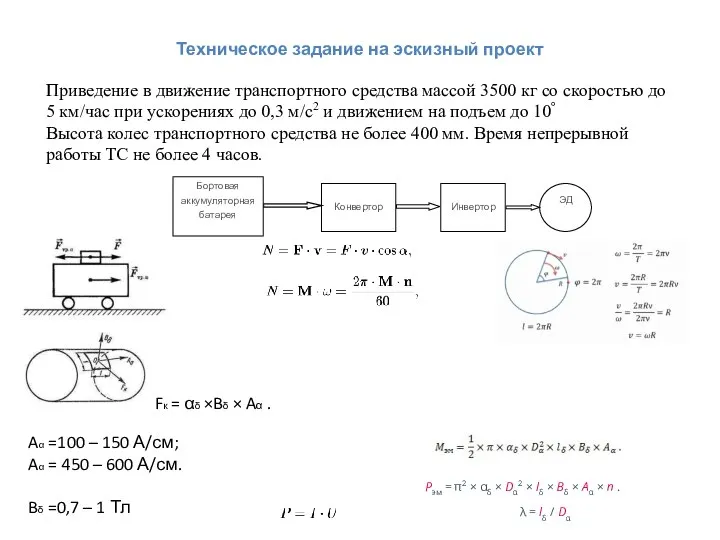 Техническое задание на эскизный проект
Техническое задание на эскизный проект Проекционный аппарат
Проекционный аппарат Наблюдение за горящей свечой. Практическая работа
Наблюдение за горящей свечой. Практическая работа Устройство карданной передачи, разработка технологической карты
Устройство карданной передачи, разработка технологической карты Презентация "Сила упругости"
Презентация "Сила упругости" Исследование короткого замыкания как основной причины возникновения пожаров
Исследование короткого замыкания как основной причины возникновения пожаров Классификация специальных электрических машин
Классификация специальных электрических машин Магнитное поле в веществе. Лекция 18
Магнитное поле в веществе. Лекция 18 Закон сохранения и превращения энергии в механических и тепловых процессах.
Закон сохранения и превращения энергии в механических и тепловых процессах.  Заземляющие устройства в установках высокого напряжение. (Лекция 17)
Заземляющие устройства в установках высокого напряжение. (Лекция 17) Сила тока. Амперметр. Измерение силы тока
Сила тока. Амперметр. Измерение силы тока Service Training, VK-21
Service Training, VK-21 Сверхминиатюрные излучатели на основе полупроводниковых наноструктур
Сверхминиатюрные излучатели на основе полупроводниковых наноструктур Програмна реалізація фрактальної моделі броунівського руху
Програмна реалізація фрактальної моделі броунівського руху Корпускулярно-волновой дуализм света
Корпускулярно-волновой дуализм света Валы и подшипники
Валы и подшипники Роль радиотехники в развитии науки
Роль радиотехники в развитии науки Электромагнитные пушки: Рельсотрон
Электромагнитные пушки: Рельсотрон Решение задач по теме: «Давление в жидкости»
Решение задач по теме: «Давление в жидкости» Уравнение Шредингера Лекция 7
Уравнение Шредингера Лекция 7  Конденсатор филворд по физике
Конденсатор филворд по физике Великий сын России. 19 ноября 2011 года Россия отмечала 300 лет со дня рождения выдающегося ученого, титана человеческой мысли, насто
Великий сын России. 19 ноября 2011 года Россия отмечала 300 лет со дня рождения выдающегося ученого, титана человеческой мысли, насто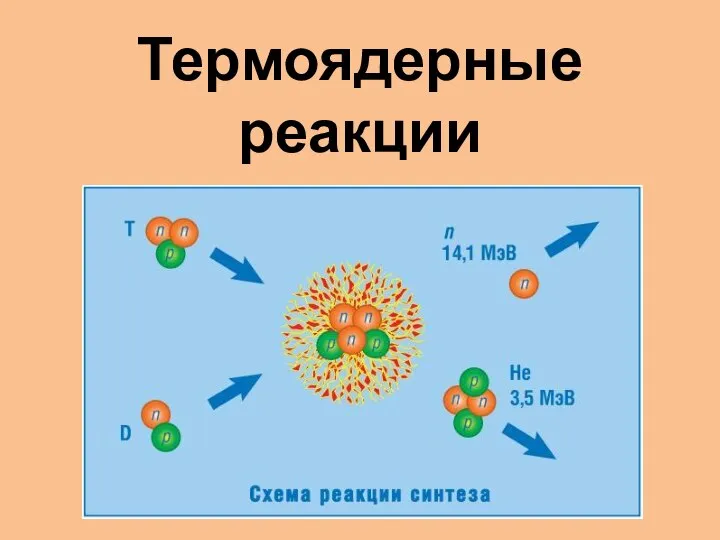 Термоядерные реакции
Термоядерные реакции Физика в быту
Физика в быту Основы гидравлики
Основы гидравлики Аеродинаміка та динаміка польоту літака. Аеродинамічні характеристики крила. (Лекція 5.2.1)
Аеродинаміка та динаміка польоту літака. Аеродинамічні характеристики крила. (Лекція 5.2.1)