Содержание
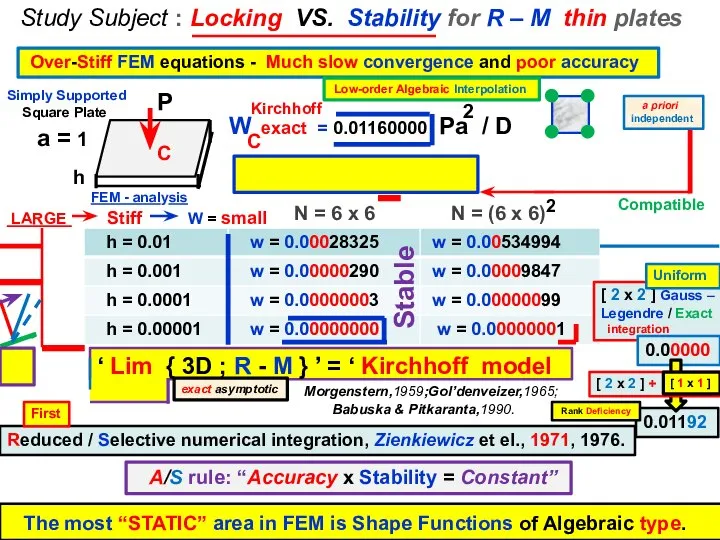
- 2. Study Subject : Locking VS. Stability for R – M thin plates N = 6 x
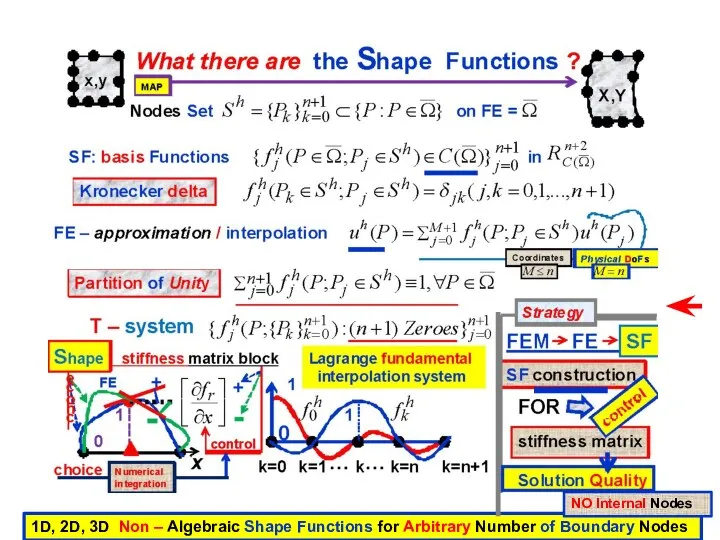
- 3. 1D, 2D, 3D Non – Algebraic Shape Functions for Arbitrary Number of Boundary Nodes NO Internal
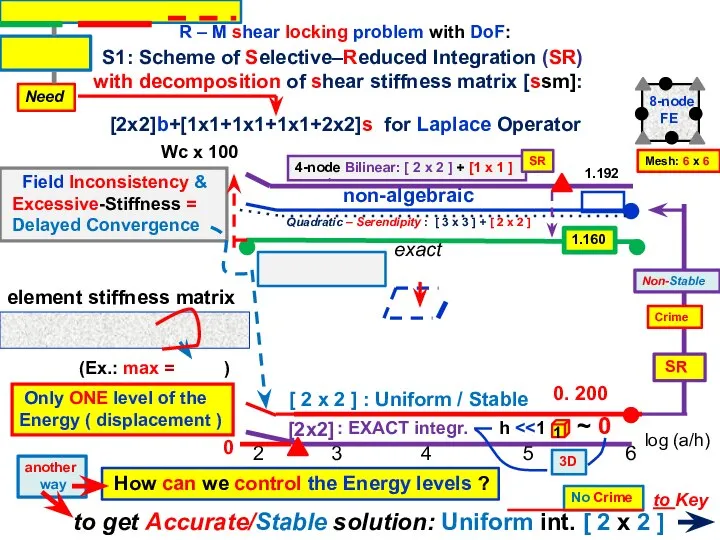
- 4. S1: Scheme of Selective–Reduced Integration (SR) with decomposition of shear stiffness matrix [ssm]: [2x2]b+[1x1+1x1+1x1+2x2]s for Laplace
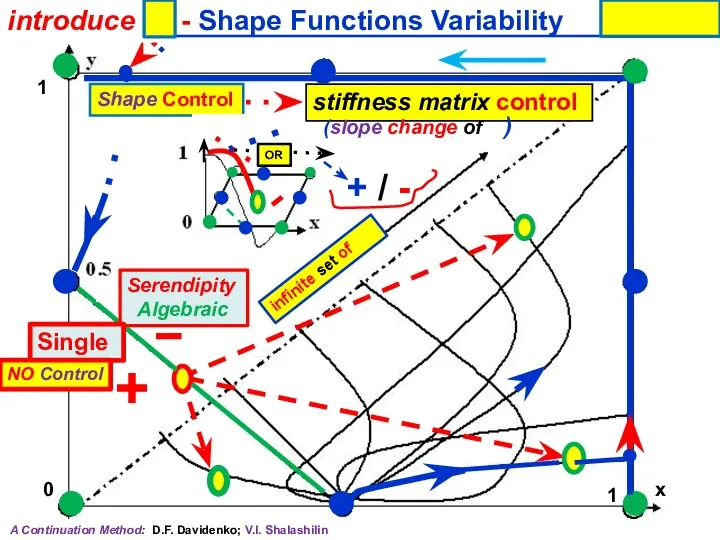
- 5. x Shape Control stiffness matrix control (slope change of ) 1 0 1 + Serendipity Algebraic
- 6. : Scheme of Full (Uniform) Integration (FI): [2x2] for Helmholtz Operator 0 2 3 4 5
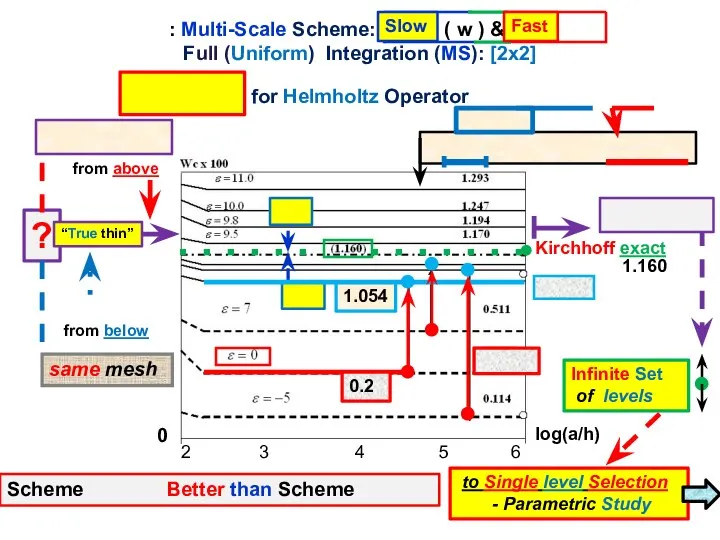
- 7. : Multi-Scale Scheme: Slow ( w ) & Fast Full (Uniform) Integration (MS): [2x2] for Helmholtz
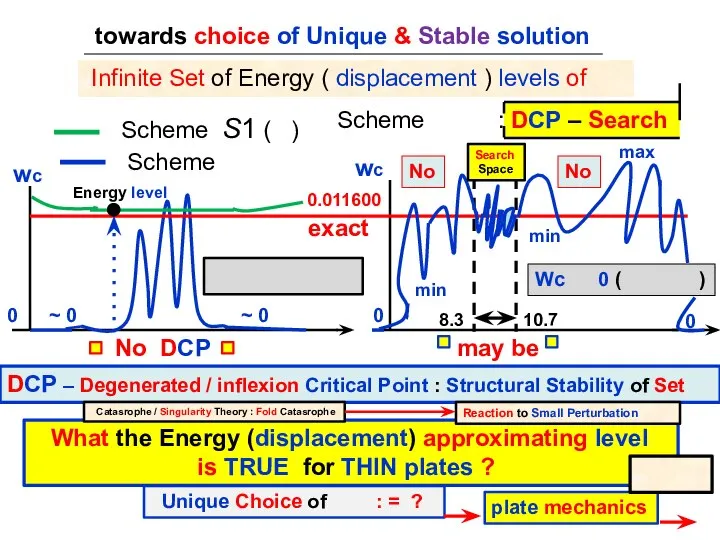
- 8. towards choice of Unique & Stable solution Scheme Scheme : wc 0 exact wc 0 No
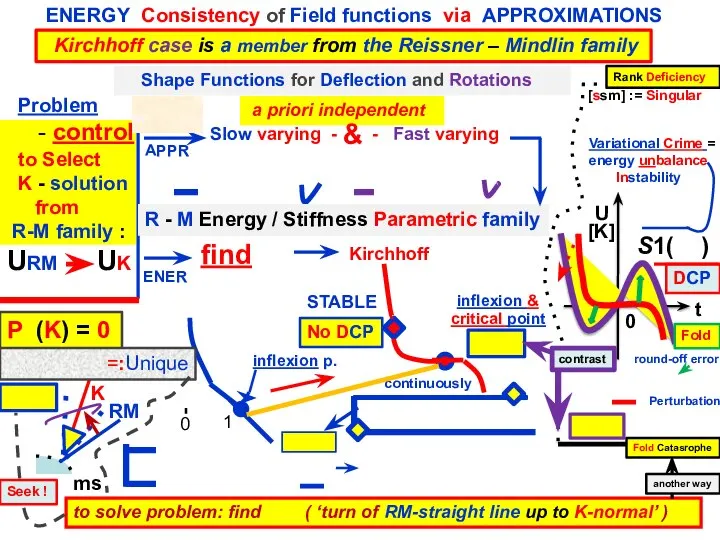
- 9. to solve problem: find ( ‘turn of RM-straight line up to K-normal’ ) 1 0 U
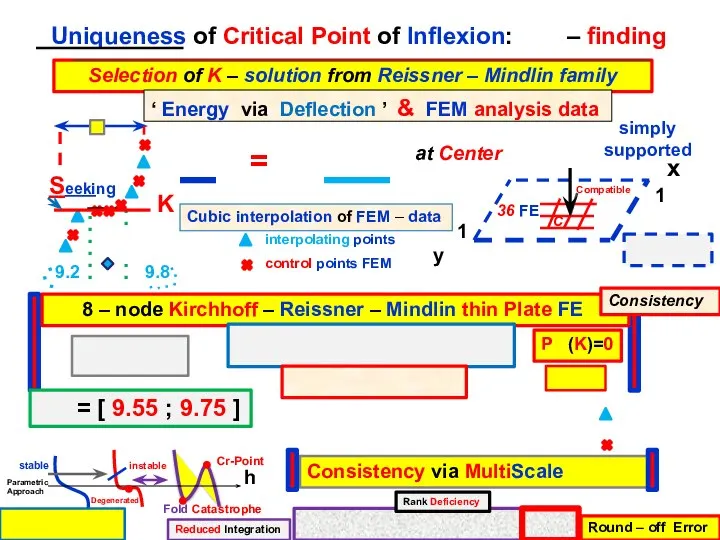
- 10. (i = 1, 2) interpolating points control points FEM Cubic interpolation of FEM – data 9.2
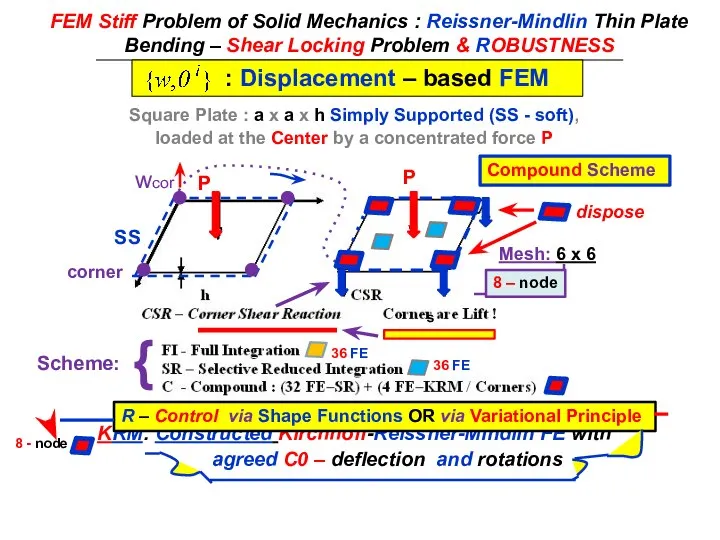
- 11. FEM Stiff Problem of Solid Mechanics : Reissner-Mindlin Thin Plate Bending – Shear Locking Problem &
- 12. Convergence Improving (Quality Control) Nondimensional Deflection at with varying (a/h) ratios K-RM solution: Sch. stable =
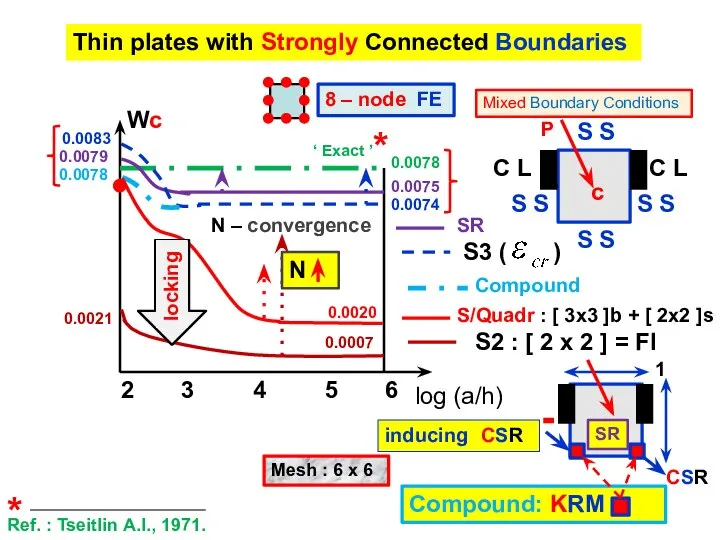
- 13. Thin plates with Strongly Connected Boundaries 2 6 3 4 5 S S C L C
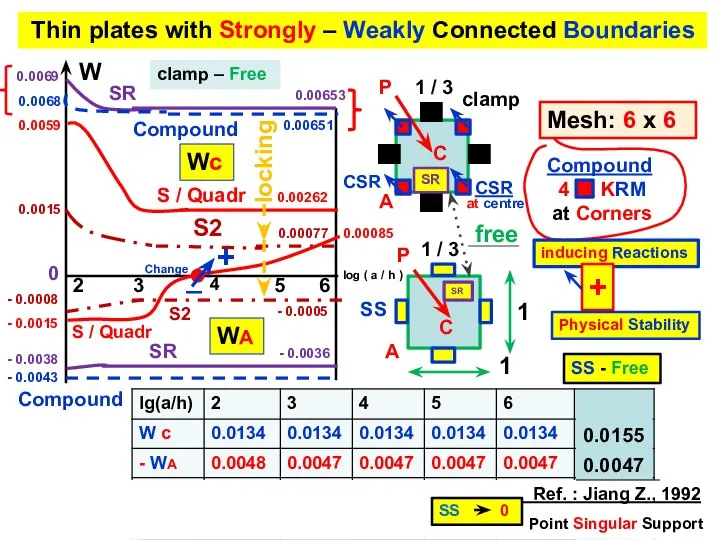
- 14. Thin plates with Strongly – Weakly Connected Boundaries 2 3 4 5 6 0.0155 0.0047 C
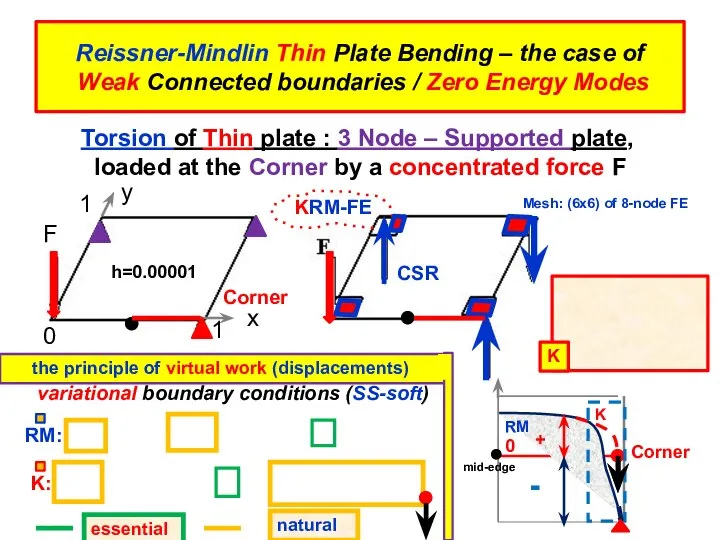
- 15. Reissner-Mindlin Thin Plate Bending – the case of Weak Connected boundaries / Zero Energy Modes Mesh:
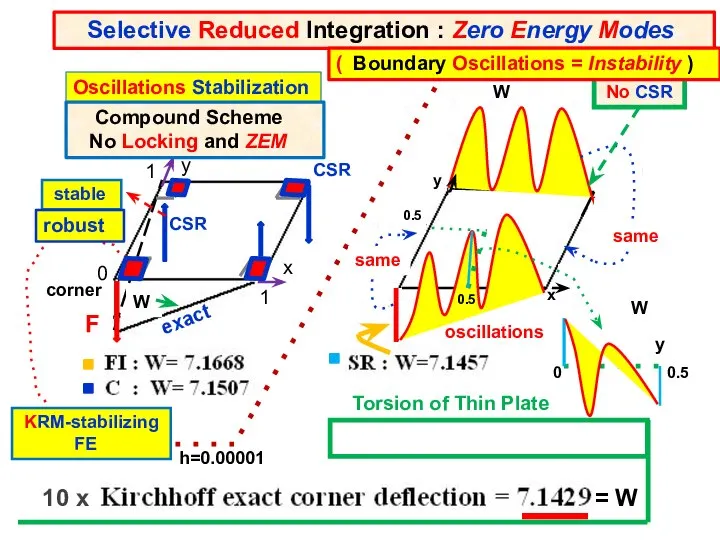
- 16. corner 1 y 1 0 x same same No CSR 0 0.5 y W 0.5 x
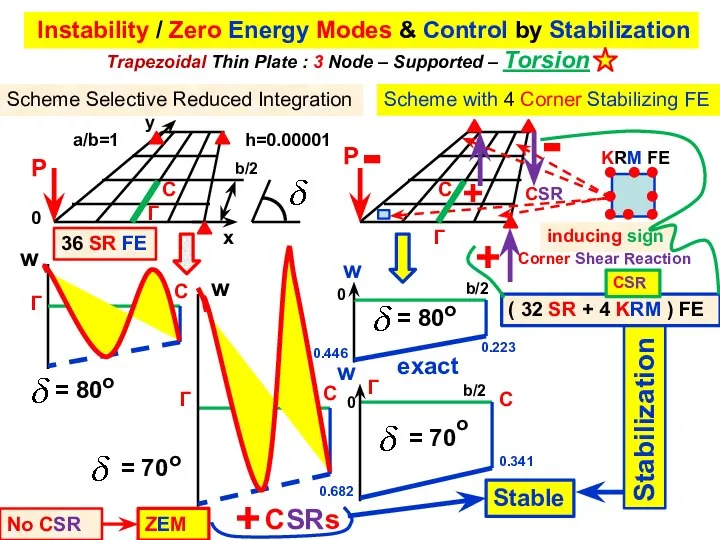
- 17. Trapezoidal Thin Plate : 3 Node – Supported – Torsion Instability / Zero Energy Modes &
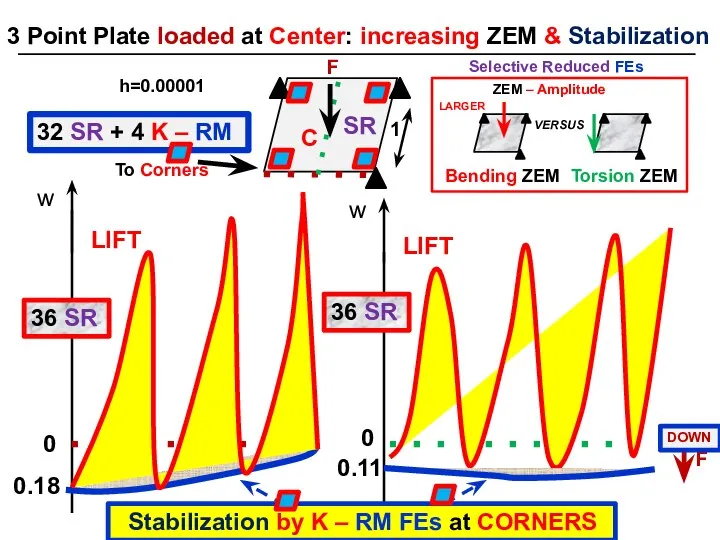
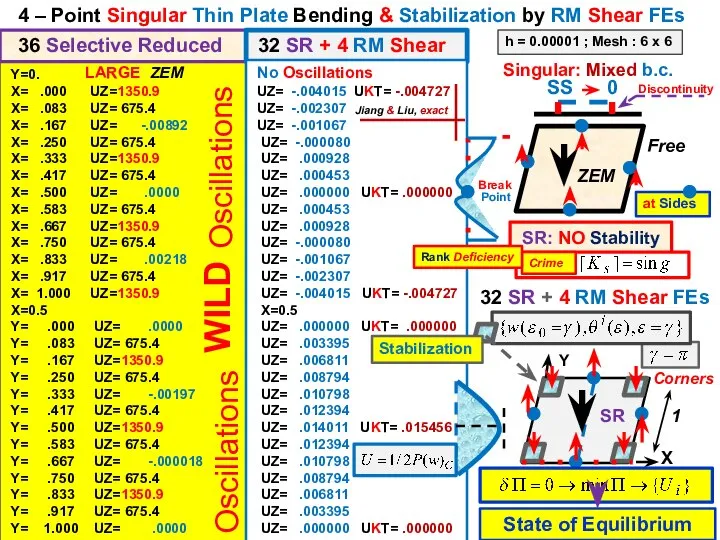
- 18. 3 Point Plate loaded at Center: increasing ZEM & Stabilization 32 SR + 4 K –
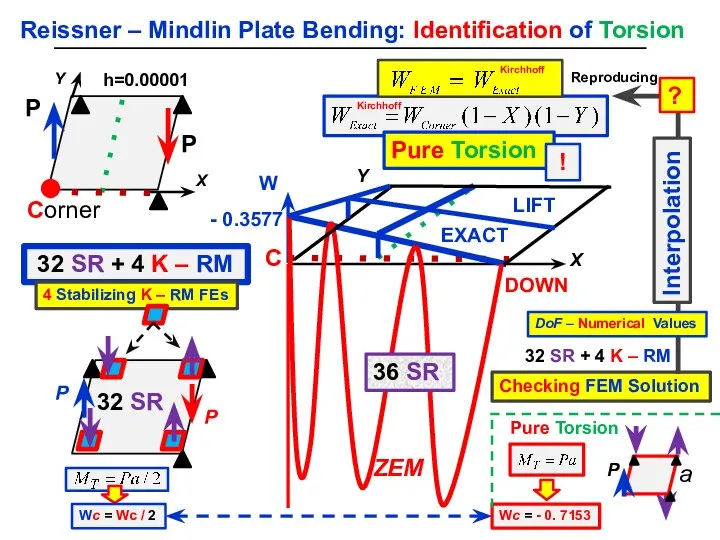
- 19. Reissner – Mindlin Plate Bending: Identification of Torsion 32 SR + 4 K – RM Corner
- 20. Y=0. X= .000 UZ=1350.9 X= .083 UZ= 675.4 X= .167 UZ= -.00892 X= .250 UZ= 675.4
- 22. Скачать презентацию
![: Scheme of Full (Uniform) Integration (FI): [2x2] for Helmholtz Operator](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1472332/slide-5.jpg)

 Презентація на тему “Атомна (ядерна) енергетика” Виконали Учениці 10-А класу Черкаської загальноосвітньої школи І-ІІІ ст. №30 Воловодівська Ольга та Шевченко Анна
Презентація на тему “Атомна (ядерна) енергетика” Виконали Учениці 10-А класу Черкаської загальноосвітньої школи І-ІІІ ст. №30 Воловодівська Ольга та Шевченко Анна  Спектральный анализ
Спектральный анализ Теория Большого Взрыва
Теория Большого Взрыва Законы сохранения и изменения момента импульса в механике
Законы сохранения и изменения момента импульса в механике Наблюдения и опыты. Задачи физики
Наблюдения и опыты. Задачи физики Электрический ток в газах
Электрический ток в газах Динамика кулисного механизма
Динамика кулисного механизма Плоская и пространственная система сил
Плоская и пространственная система сил Измерение физических величин. Погрешности измерений
Измерение физических величин. Погрешности измерений Лазерная техника и технология
Лазерная техника и технология Поверхностные явления. Лекция 15
Поверхностные явления. Лекция 15 Классификация нелинейных элементов и цепей
Классификация нелинейных элементов и цепей Научно-исследовательская работа по физике на тему: Силы
Научно-исследовательская работа по физике на тему: Силы Центральный музей связи имени А.С. Попова
Центральный музей связи имени А.С. Попова Автоколлимационный микроскоп. Динаметр. Гониометр
Автоколлимационный микроскоп. Динаметр. Гониометр Кептіру процесі
Кептіру процесі Тема урока. «Связь между давлением и объемом газа при постоянной температуре». 8 класс
Тема урока. «Связь между давлением и объемом газа при постоянной температуре». 8 класс Қатты денелердің механикалық қозалысы
Қатты денелердің механикалық қозалысы Електричний струм у газах
Електричний струм у газах Презентацию создал: Ученик 8 класса «Б» АМБОУСОШ №4 Города Асбеста Свердл. Обл. Матяж Денис
Презентацию создал: Ученик 8 класса «Б» АМБОУСОШ №4 Города Асбеста Свердл. Обл. Матяж Денис Атомно-эмиссионный спектрометр с индуктивно связанной плазмой ICPE-9000
Атомно-эмиссионный спектрометр с индуктивно связанной плазмой ICPE-9000 Гигиеническое значение электромагнитных полей
Гигиеническое значение электромагнитных полей Масс-спектрометрия и хромато-масс-спектрометрия высокого разрешения
Масс-спектрометрия и хромато-масс-спектрометрия высокого разрешения Законы преломления света 8 класс Выполнила: учитель физики МОУ «СОШ №6» г. Кирова Калужской области Кочергина В.Э. 2010 год
Законы преломления света 8 класс Выполнила: учитель физики МОУ «СОШ №6» г. Кирова Калужской области Кочергина В.Э. 2010 год  Генератор переменного тока. (11 класс)
Генератор переменного тока. (11 класс) Конденсаторы
Конденсаторы Демонстрационный эксперимент по геометрической оптике Выполнил: Ригачев Илья Ученик 9 «А» класса Научный руководитель: Федот
Демонстрационный эксперимент по геометрической оптике Выполнил: Ригачев Илья Ученик 9 «А» класса Научный руководитель: Федот Волновые уравнения Максвелла
Волновые уравнения Максвелла