Содержание
- 2. 163 ВОПРОСЫ 34. Термодинамика. Основное уравнение молекулярно-кинетической теории. 35. Первое начало термодинамики и его применение к
- 3. 163 Вопрос № 34. Термодинамика. Основное уравнение молекулярно-кинетической теории. Термодинамическая температура.
- 4. 163 Предварительные сведения Статистическая физика – раздел физики, посвящённый изучению свойств макроскопических тел, исходя из свойств
- 5. 163 Термодинамика изучает свойства макроскопических тел и протекающие в них процессы, не вдаваясь в микроскопическую природу
- 6. 163 Статистическая система – система из большого числа частиц. Статистический ансамбль – система из большого числа
- 7. 163 Элементы термодинамики Термодинамическая система – совокупность макроскопических тел, которые могут обмениваться энергией между собой и
- 8. 163 Если система не обменивается энергией с внешней средой, то она называется замкнутой или изолированной. Неравновесное
- 9. 163 Равновесное состояние – состояние в котором все параметры состояния имеют определённые значения, не изменяющиеся с
- 10. 163 Физические величины: Количество вещества (ν) – число молей; Моль - количество вещества, содержащее число Авогадро
- 11. 163 Статистическая физика описывает каждую частицу для описания всей системы, если частиц N, то получим N
- 12. 163 Термодинамика же оперирует средними значениями, которые выражаются в параметрах состояния: объём (V, м3), давление (p,
- 13. 163 Уравнение состояния – это соотношение, определяющее связь между параметрами состояния какого-либо тела. Идеальный газ –
- 14. 163 Уравнение состояния идеального газа (уравнение Менделеева-Клапейрона)
- 15. 163 R = k * NА = 8,31 Дж/моль*К – универсальная газовая постоянная, k = 1,38
- 16. 163 Температура – количественная характеристика внутренней энергии тела. Эта энергия не относится к механической энергии. –
- 17. 163 С учётом этого выражения можно получить основное уравнение молекулярно-кинетической теории
- 18. 163 Температуру тела определяют путём сравнения с температурой другого тела или через другие параметры, которые зависят
- 19. 163 Термодинамическая температура – температура определяющая внутреннюю энергию тела. Если энергии в молекулах нет, то и
- 20. 163
- 21. 163
- 22. 163 35. Первое начало термодинамики и его применение к изопроцессам. Уравнение Пуссона. Уравнение политропы. Работа в
- 23. 163 Температура определяет внутреннюю энергию тела. Эта энергия слагается из кинетической энергии поступательного и вращательного движения
- 24. 163 Внутреннюю энергию можно изменить двумя способами: передавая телу некоторое количество теплоты dQ (теплопередача) или совершая
- 25. 163 Первое начало термодинамики: количество теплоты, сообщённое систем, идёт на приращение внутренней энергии системы и на
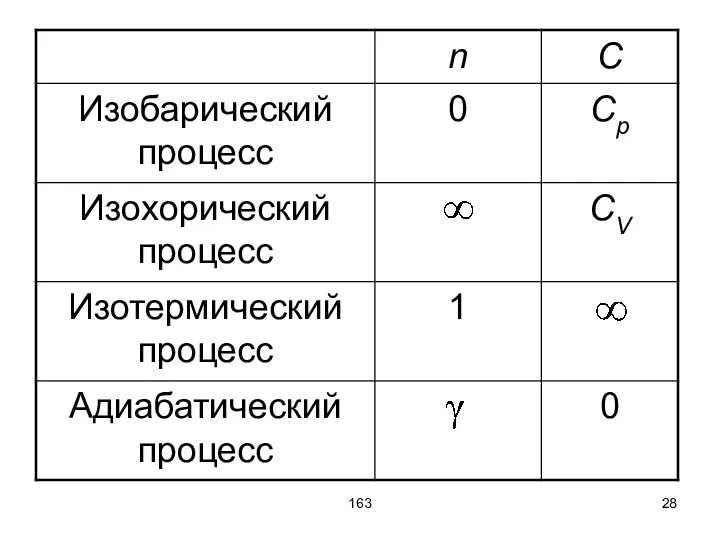
- 26. 163 Политропический процесс – процесс с постоянной теплоёмкостью. Политропический процесс описывается уравнением политропы Здесь n –
- 27. 163 С – теплоёмкость 1 моля вещества, Сp – теплоёмкость 1 моля вещества при постоянном давлении,
- 28. 163
- 29. 163 Изобарический процесс – процесс при постоянном давлении. Изохорический процесс – процесс при постоянном объёме. Изотермический
- 30. 163 Работа в случае изобарического процесса: A = pΔV. В случае изохорического процесса нет изменения объёма,
- 31. 163 Для вычисления работы в адиабатическом процессе представим зависимость давления от объёма с помощью уравнения Пуассона
- 32. 163
- 33. 163 В случае изотермического процесса получим следующее выражение
- 34. 163
- 35. 163 Вопрос № 36. Статистическая система и статистический ансамбль. Статистический вес. Энтропия. Изменение энтропии идеального газа
- 36. 163 Статистическая система – система из большого числа частиц. Статистический ансамбль – система из большого числа
- 37. 163 Рассмотрим некоторый термодинамический процесс. Система перешла из состояния «1» в состояние «2». Если мы имеем
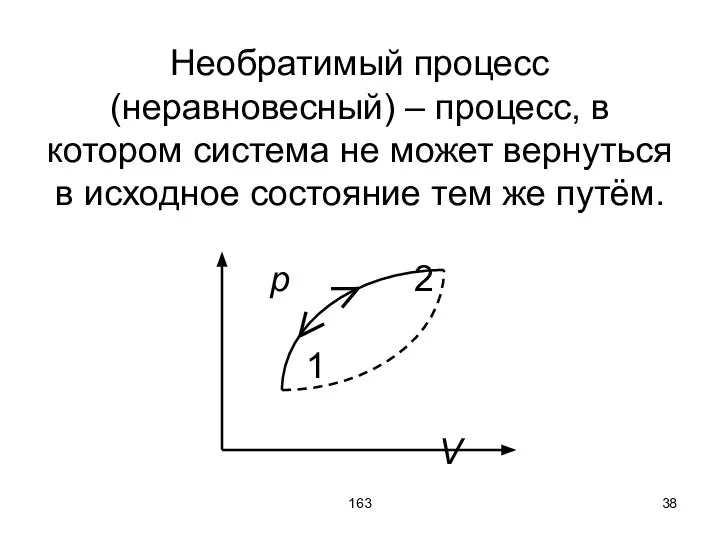
- 38. 163 Необратимый процесс (неравновесный) – процесс, в котором система не может вернуться в исходное состояние тем
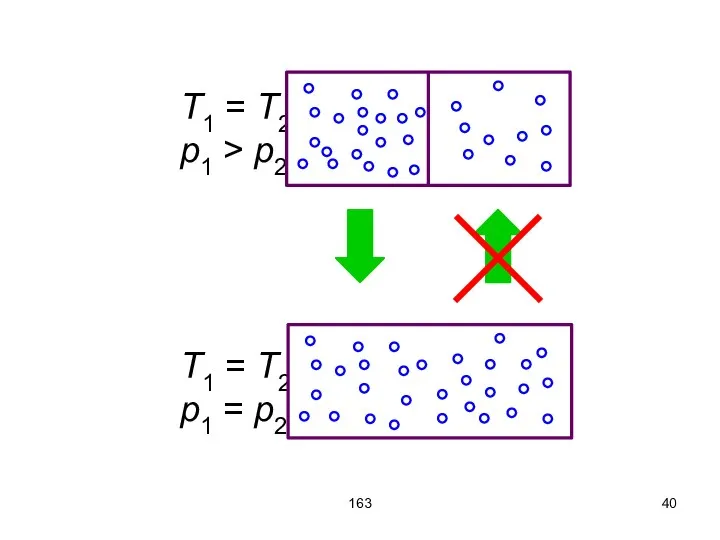
- 39. 163 О направлении процесса не всегда возможно говорить, используя только термодинамические параметры. Приведём пример. Имеется изолированная
- 40. 163 T1 = T2, p1 > p2. T1 = T2, p1 = p2.
- 41. 163 Теоретически, это событие возможно, но вероятность этого события практически равна нулю. Отсюда делаем вывод: для
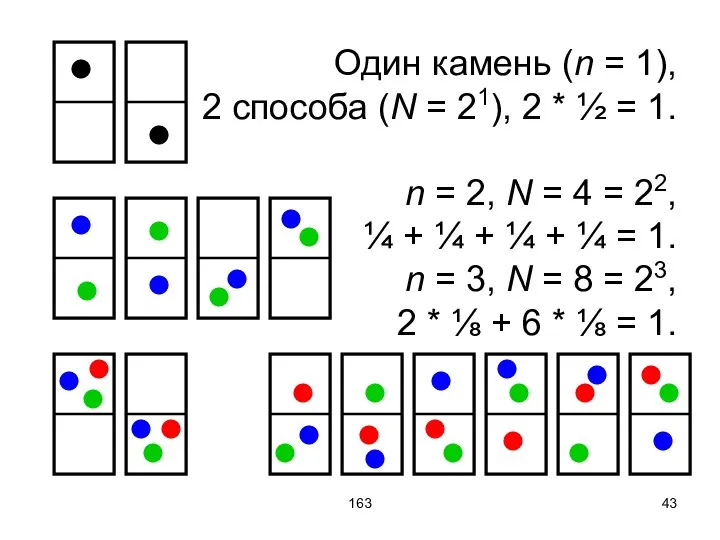
- 42. 163 Рассмотрим ящик с двумя отделами, в котором лежит один камень или два, или три и
- 43. 163 Один камень (n = 1), 2 способа (N = 21), 2 * ½ = 1.
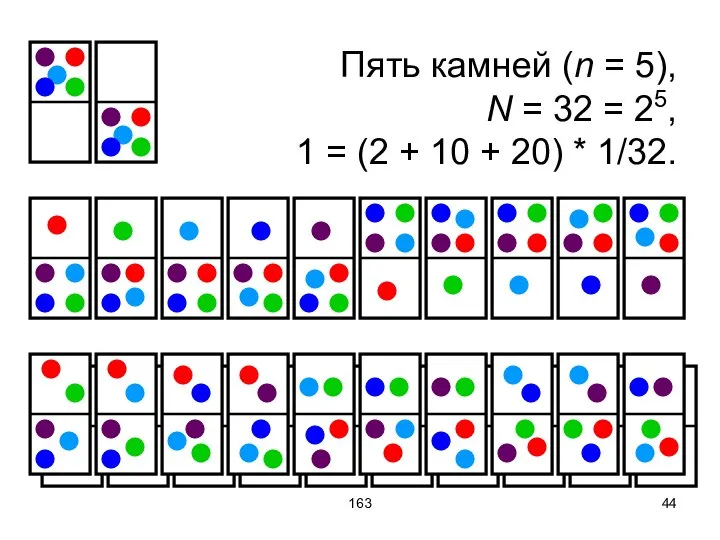
- 44. 163 Пять камней (n = 5), N = 32 = 25, 1 = (2 + 10
- 45. 163 На рисунках представлены все возможные микросостояния. Согласно эргодической гипотезе все микросостояния равновероятны. Однако, они относятся
- 46. 163 Состояние термодинамической системы также может быть задано с помощью макроскопических параметров (T, p, V). Именно
- 47. 163 Но для разных макросостояний разное число микросостояний (не важно какая именно частица находится в данном
- 48. 163 Число различных микросостояний, посредством которых осуществляется данное макросостояние, называется статистическим весом макросостояния – Ω. Для
- 49. 163 Как видно, число огромное. Энтропия – характеристика вероятности состояний (или характеристика числа состояний системы): формула
- 50. 163 Энтропия – функция состояния, следовательно, её можно выразить через параметры состояния: S0 – константа.
- 51. 163 Если процесс обратимый, то dS = dQ/T. Свойства энтропии 1) В ходе необратимого процесса энтропия
- 52. 163 Практичнее вычислять не энтропию, а её изменение. Изменение энтропии: Изобарический процесс
- 53. 163 Изотермический процесс Изохорический процесс Адиабатический процесс ΔS = 0.
- 54. 163
- 55. 163 ЛЕКЦИЯ № 13. Теорема Карно Функции распределения
- 56. 163 ВОПРОСЫ 37. Второе начало термодинамики. Тепловая смерть вселенной. Третье начало термодинамики. Теорема Карно. 38. Функция
- 57. 163 37. Второе начало термодинамики. Тепловая смерть вселенной. Третье начало термодинамики. Цикл Карно, его КПД для
- 58. 163 Элементы теории вероятности Вероятность – отношение событий с i-м исходом Ni к полному числу испытаний
- 59. 163 Если события зависимы (вероятность выпадения и «1» и «6»), то вероятности умножаются, 1/6 * 1/6.
- 60. 163 Эргодичность (эргодическая гипотеза) – все вероятности появления того или иного события равны. То есть, если
- 61. 163 Однако, при бросании 6000 раз кубика, грань «6» выпадет не 1000 раз. Это число будет
- 62. 163 Если произвести 600 бросаний кубика, то число «6» выпадет раз. В 1 см3 воздуха содержится
- 63. 163 Очевидно, что флуктуации тем незаметнее, чем большее число испытаний
- 64. 163 Второе начало термодинамики – энтропия изолированной термодинамической системы может только возрастать либо по достижении максимального
- 65. 163 Если процесс обратимый, то энтропия не изменяется Если процесс необратимый, то Эти уравнения можно объединить
- 66. 163 Исходя из законов термодинамики (второе начало термодинамики) Клаузиус пришёл к выводу, что рано или поздно
- 67. 163 Тепловая смерть вселенной не реализуема ещё по одной причине, из-за флуктуаций. Вселенная огромна, следовательно, флуктуации
- 68. 163 Третье начало термодинамики (теорема Нернста) – энтропия любого тела стремится к нулю при стремлении к
- 69. 163 Теорема Карно – коэффициент полезного действия всех обратимых машин, работающих в идентичных условиях (т.е. при
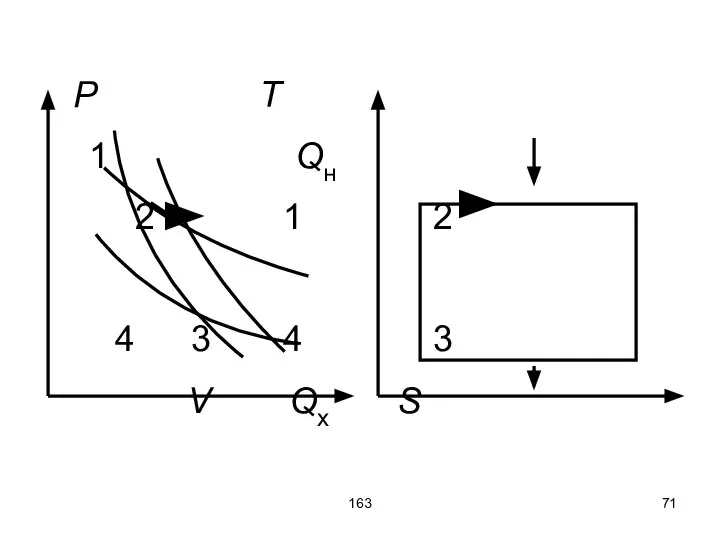
- 70. 163 Цикл Карно – цикл, состоящий из двух изотермических процессов и двух адиабатических процессов. Этот цикл
- 71. 163 P T 1 Qн 2 1 2 4 3 4 3 V Qх S
- 72. 163 На участке 1-2 рабочее тело получает энергию Qн от нагревателя с температурой T1 (Tн). На
- 73. 163 Коэффициент полезного действия (КПД) для реальной тепловой машины и для идеальной тепловой машины
- 74. 163
- 75. 163 38. Функция распределения Максвелла. Наиболее вероятная, средняя и среднеквадратичная скорости молекул.
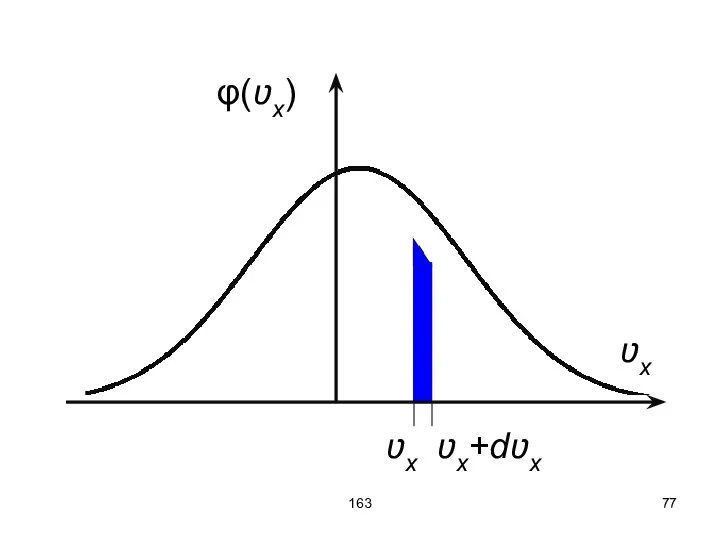
- 76. 163 Распределение Максвелла Распределение по составляющей скорости – плотность вероятности для распределения частиц по ʋx: здесь
- 77. 163 φ(ʋx) ʋx ʋx ʋx+dʋx
- 78. 163 Функции φ(ʋx), φ(ʋy), φ(ʋz) статистически независимы, поэтому можно их считать равными друг другу. Для получения
- 79. 163 Распределение по вектору скорости
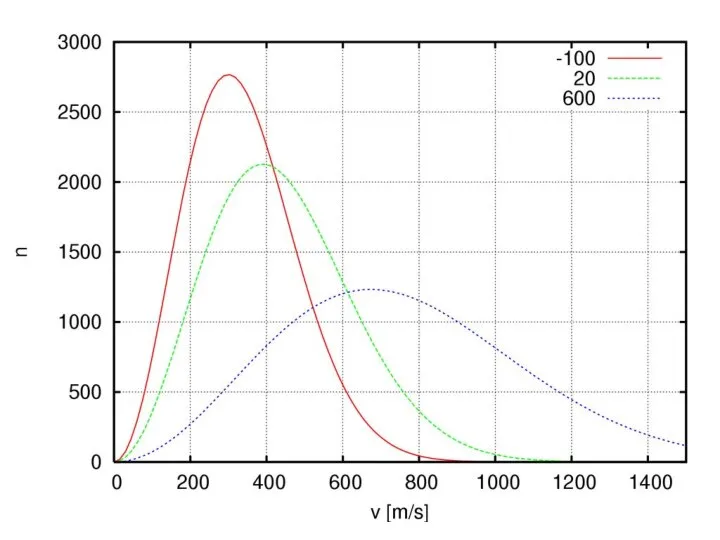
- 80. 163 Распределение по модулю скорости (распределение Максвелла)
- 81. 163
- 82. 163 Функция F(ʋ) – функция вероятности. Именно, F(ʋ)dʋ – есть вероятность найти молекулу со скоростью в
- 83. 163 Наивероятнейшая скорость (находится из производной функции по скорости dF(ʋ)/dʋ = 0) Средняя скорость Среднеквадратичная скорость
- 84. 163
- 85. 163 Вопрос № 39. Барометрическая формула Больцмана. Распределение Гиббса.
- 86. 163 Барометрическая формула (формула Больцмана)
- 87. 163 Здесь p, n – давление и концентрация на высоте h, p0, n0 – давление и
- 88. 163 Распределение Гиббса Для полного описания состояния термодинамического равновесия физической системы (любого тела) используется распределение Гиббса,
- 89. 163 В классической механике состояние системы N частиц полностью задано 6N – переменными (импульсами и координатами:
- 90. 163 В квантовомеханическом распределении производят распределение по уровням энергии εi. Уровни энергии бывают кратными (вырожденными) –
- 91. 163 Простые (невырожденные) – все значения энергии разные. Будем полагать все уровни невырожденными. Найдём такое распределение
- 92. 163 Учтём также следующие условия. Постоянство количество частиц: N1 + N2 + … + Nm =
- 93. 163 Пропуская вывод, запишем данное распределение частиц по энергиям Это распределение Максвелла-Больцмана или каноническое распределение Гиббса.
- 94. 163 Функции распределения Ферми-Дирака и Бозе-Эйнштейна
- 95. 163 Согласно современной квантовой механике все элементарные и сложные частицы разделяются на два класса:
- 96. 163 1-й класс: электроны, протоны, нейтроны и все частицы с полуцелым спином. Эти частицы подчиняются статистике
- 97. 163 В статистике Ферми-Дирака принимается, что в каждом квантовом состоянии может находиться не более одной частицы.
- 98. 163 Распределение Больцмана (классические частицы). 2 частицы в 3-х разных варианта (три ячейки). 9 возможных вариантов,
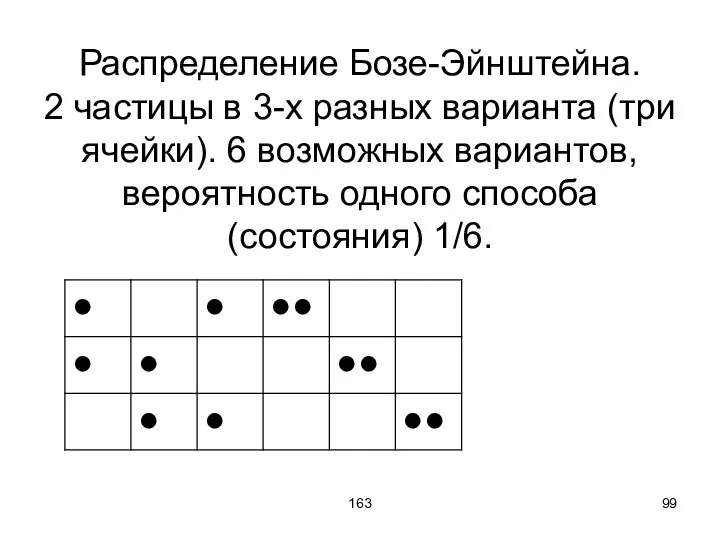
- 99. 163 Распределение Бозе-Эйнштейна. 2 частицы в 3-х разных варианта (три ячейки). 6 возможных вариантов, вероятность одного
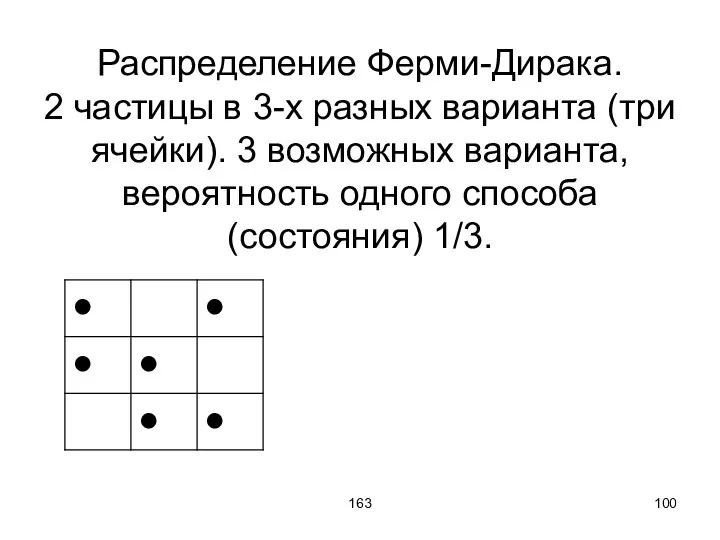
- 100. 163 Распределение Ферми-Дирака. 2 частицы в 3-х разных варианта (три ячейки). 3 возможных варианта, вероятность одного
- 101. 163 Число способов, которыми можно распределить Ni число частиц по Zi квантовым состояниям i-го слоя, будет:
- 102. 163 Законы распределения Фермионы Бозоны – среднее число частиц приходящееся на одно квантовое состояние.
- 103. 163 μ – химический потенциал, определяется из условия нормировки здесь N – полное число частиц.
- 104. 163 Справка Элементы комбинаторики Перестановка Размещения из n по m (n ≥ m) Сочетания из n
- 105. 163
- 106. 163 Вопрос № 40. Степени свободы. Внутренняя энергия системы. Теплоёмкость, уравнение Майера. Теорема о равнораспределении энергии
- 107. 163 Закон равнораспределения Больцмана: на каждую степень свободы молекулы приходится в среднем одинаковая кинетическая энергия, равная
- 108. 163 Средняя энергия молекулы E0 = i/2 kT, i = nпост + nвр + 2 nколеб
- 109. 163 Внутренняя энергия идеального газа Теплоёмкость молярная – это количество энергии, необходимое для нагревания одного моля
- 110. 163 Теплоёмкость молярная при постоянном объёме Теплоёмкость молярная при постоянном давлении Показатель адиабаты
- 111. 163 Уравнение Майера Теплоёмкость одного моля при постоянном давлении больше теплоёмкости одного моля при постоянном объёме
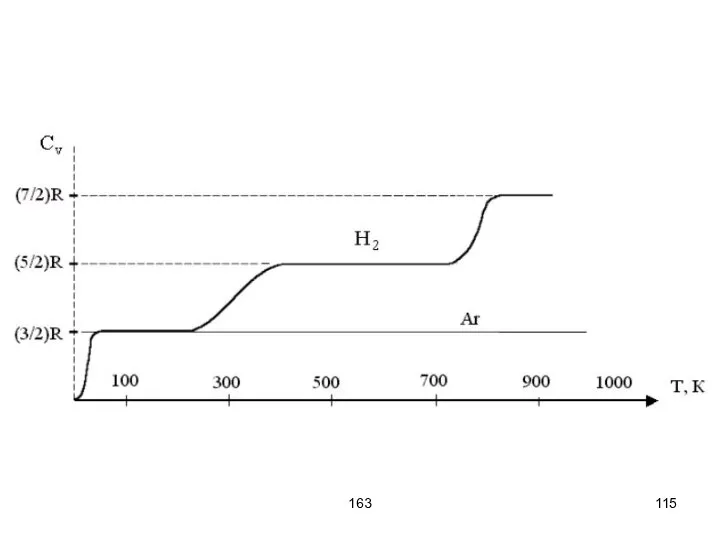
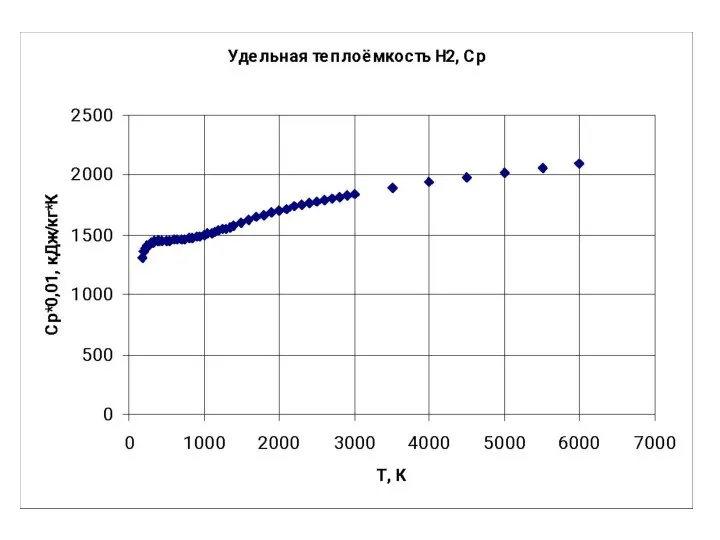
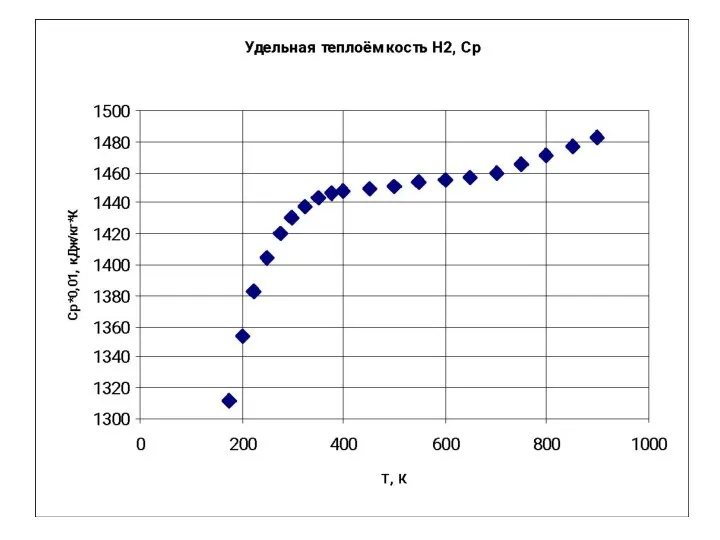
- 112. 163 Реальная теплоёмкость отличается от теоретических расчётов. Более точные значения даёт квантовая теория. Поступательная энергия не
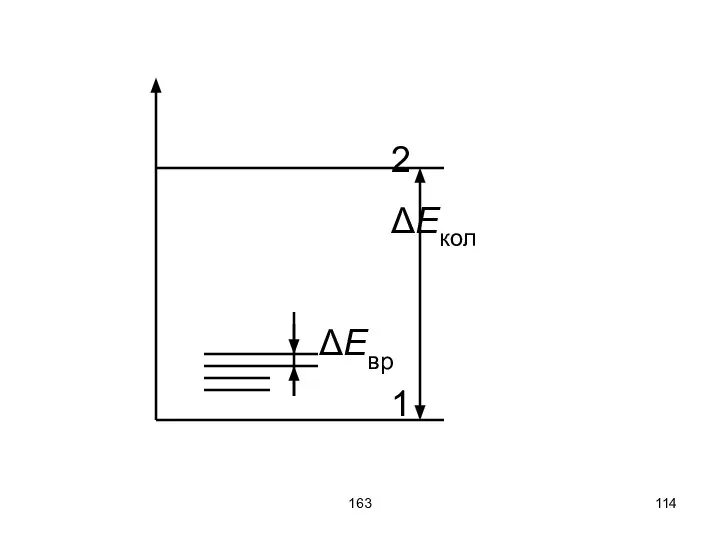
- 113. 163 Вращательная и колебательная энергии квантуются. Квант вращательной энергии много меньше кванта колебательной энергии. Поэтому при
- 114. 163 2 ΔEкол ΔEвр 1
- 115. 163
- 116. 163
- 117. 163
- 118. 163
- 119. 163 ЛЕКЦИЯ 14. Реальные газы. Уравнение Ван-дер-Ваальса.
- 120. 163 ВОПРОСЫ 41. Реальные газы. Уравнение Ван-дер-Ваальса. Изотермы Ван-дер-Ваальса. Критическая точка. 42. Фазы и условия равновесия
- 121. 163 Вопрос № 41. Реальные газы. Уравнение Ван-дер-Ваальса. Изотермы Ван-дер-Ваальса. Критическая точка.
- 122. 163 Уравнение состояния идеального газа pV = m/M RT описывает поведение достаточно разреженных газов. Реально, приходится
- 123. 163 Наиболее точно описывает поведение реальных газов уравнение Ван-дер-Ваальса: Для одного моля и для ν молей.
- 124. 163 Здесь b выражает объём молекул одного моля, a выражает силу взаимодействия молекул.
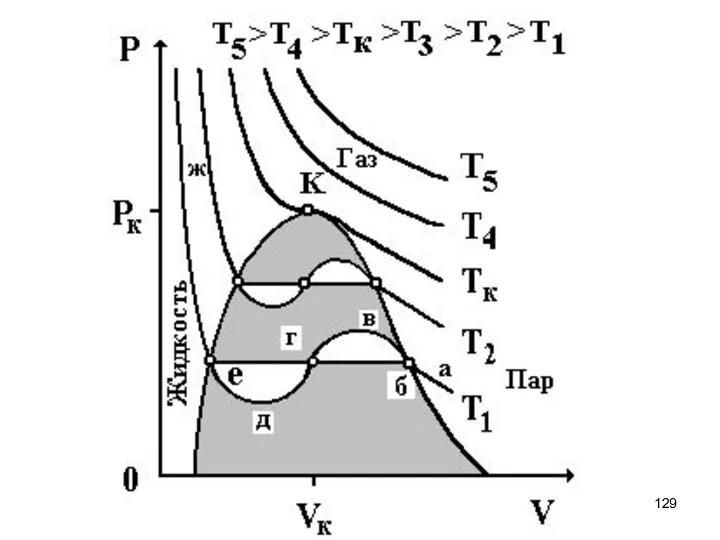
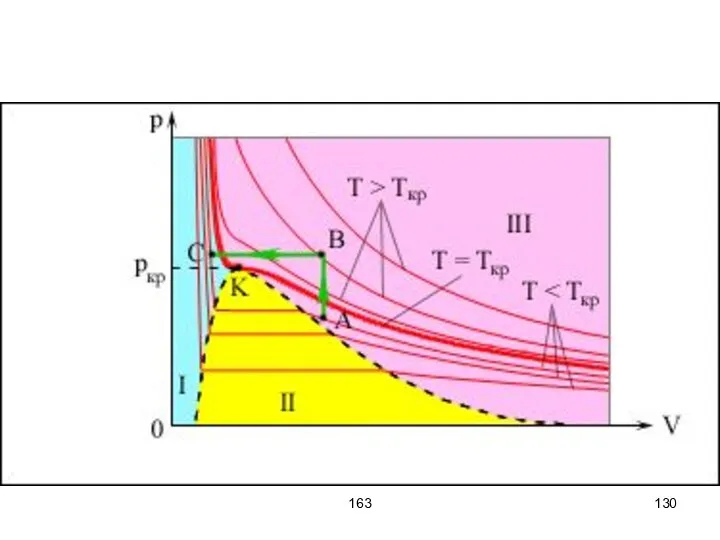
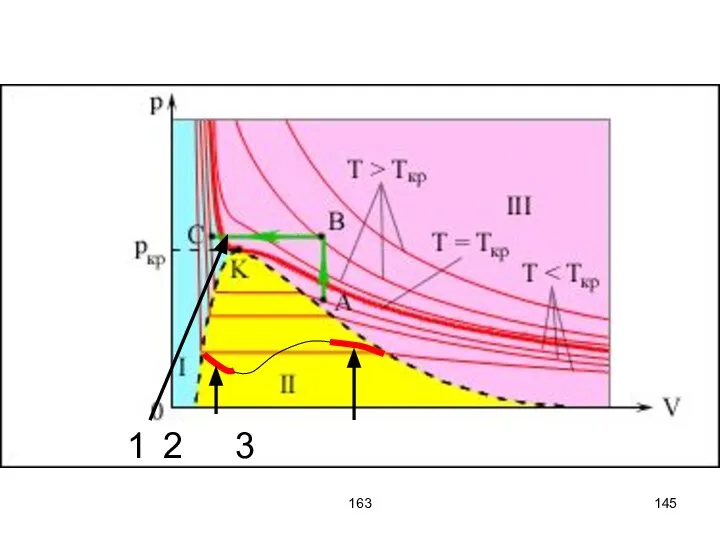
- 125. 163 Изотермы Ван-дер-Ваальса Получим зависимость давления p от объёма V при постоянной температуре. Для удобства перепишем
- 126. 163 Продифференцируем выражение Ван-дер-Ваальса дважды (T = const)
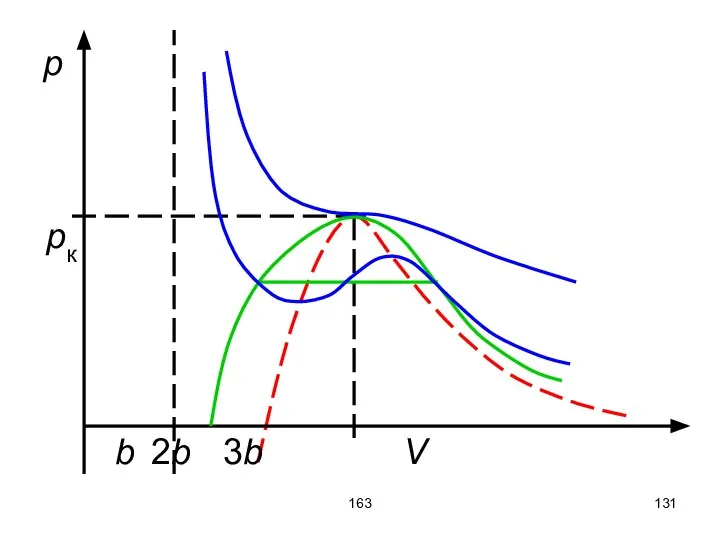
- 127. 163 Во второй производной мы пришли к значению критического объёма (экстремум функции) Vк = 3b. Используя
- 128. 163 В точке К кривая экстремумов (первая производная) сама имеет экстремум (здесь min и max Ван-дер-Ваальсовской
- 129. 163
- 130. 163
- 131. 163 p pк b 2b 3b V
- 132. 163 Горизонтальный участок проводится таким образом, чтобы площади, ограниченные кривой и горизонтальной линией были равны. Внутренняя
- 133. 163
- 134. 163 Вопрос № 42. Фазы и условия равновесия фаз. Фазовые превращения. Уравнение Клапейрона-Клаузиуса.
- 135. 163 Фазовые превращения Уравнение Ван-дер-Ваальса хорошо описывает переход вещества из одного агрегатного состояния в другое –
- 136. 163 Фазовый переход 1-го рода – переход вещества из одной фазы в другую с поглощением или
- 137. 163 Испарение – переход жидкости в газ. Конденсация – переход газа в жидкость. Сублимация (возгонка) –
- 138. 163 Рассмотрим герметичный сосуд с некоторым количеством жидкости. Наиболее быстрые (энергичные, горячие) молекулы могут покинуть жидкость
- 139. 163 Если число молекул, покинувших жидкость равно числу молекул вернувшихся за один и тот же период,
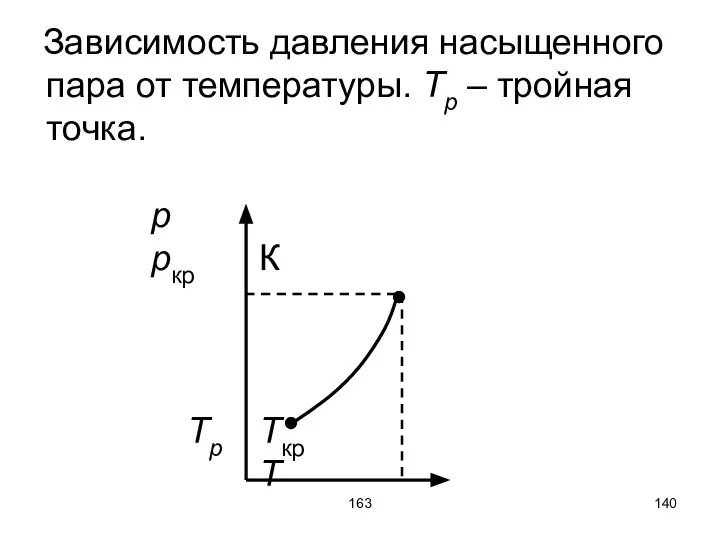
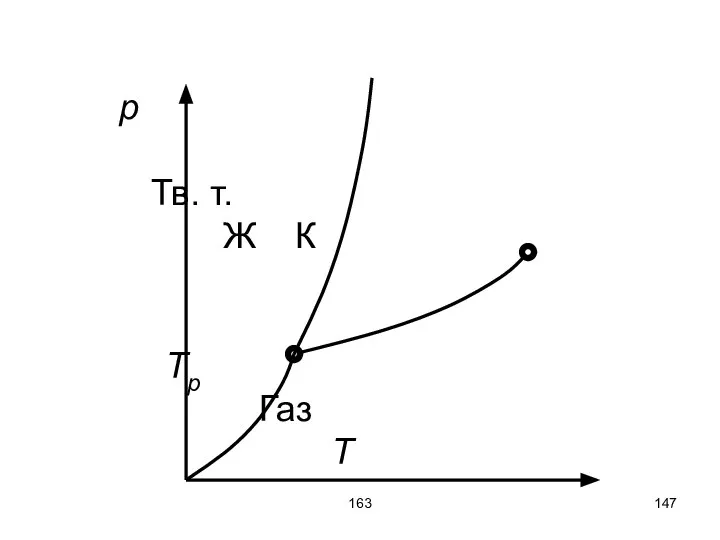
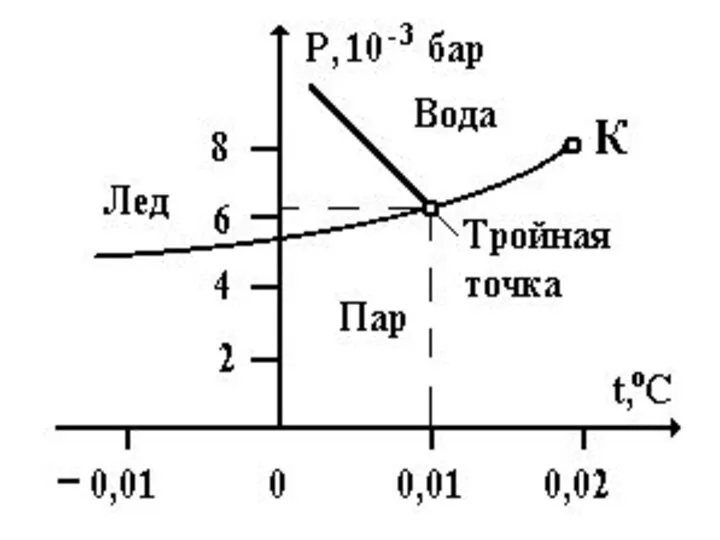
- 140. 163 Зависимость давления насыщенного пара от температуры. Tp – тройная точка. p pкр К Tp Tкр
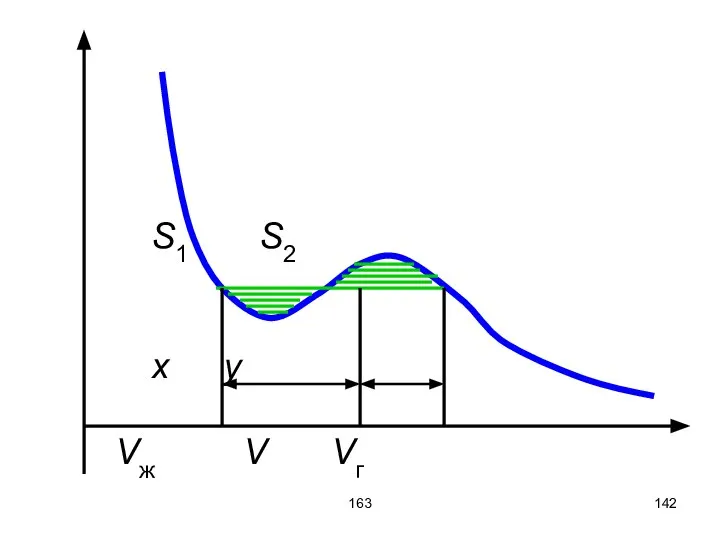
- 141. 163 На изотерме Ван-дер-ваальсовского газа процессу испарения или конденсации соответствует горизонтальный участок. Его проводят так, чтобы
- 142. 163 S1 S2 x y Vж V Vг
- 143. 163 В случае испарения или конденсации справедливо уравнение Клапейрона-Клаузиуса здесь q – теплота фазового перехода для
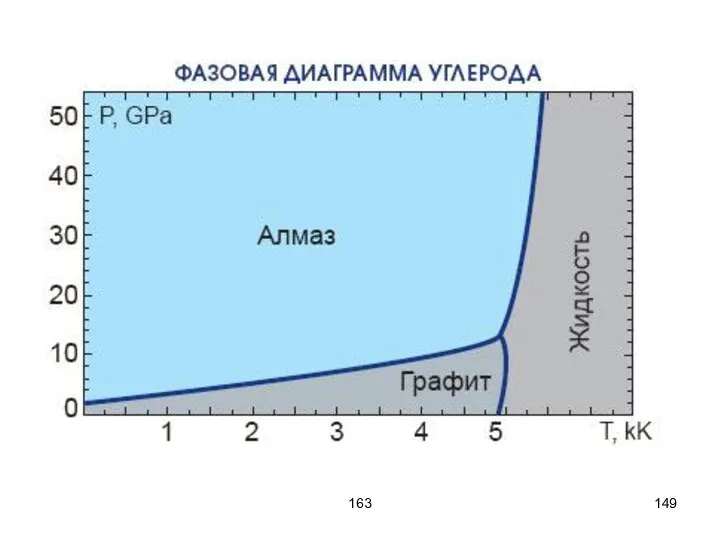
- 144. 163 Фазовые диаграммы 1) Переход из одной фазы в другую без расслаивания на две фазы, вещество
- 145. 163 1 2 3
- 146. 163 Tp – тройная точка на фазовой диаграмме определяет условия, при которых могут находиться в равновесии
- 147. 163 p Тв. т. Ж К Tp Газ T
- 148. 163
- 149. 163
- 150. 163
- 151. 163 Вопрос № 43. Поверхностные явления. Коэффициент поверхностного натяжения. Формула Лапласа. Смачивание.
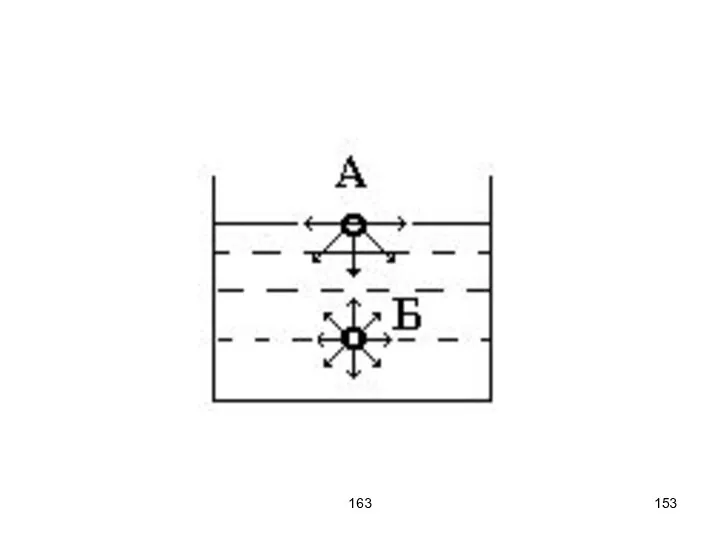
- 152. 163 Равнодействующая сил притяжения, действующих на молекулу поверхностного слоя, направлена внутрь жидкости. Это означает, что такая
- 153. 163
- 154. 163 Поэтому поверхностные явления особую роль играют, когда отношение поверхности к объёму велико (т.е. малые размеры
- 155. 163 Коэффициент поверхностного натяжения равен отношению силы, действующей на некоторый участок перпендикулярно к нему, к величине
- 156. 163 Формула Лапласа Вычислим добавочное давление в пузырьке жидкости через энергию на примере цилиндра. Изменим радиус
- 157. 163 Изменение объёма Работа сил избыточного давления (она же есть изменение энергии ΔA = – ΔW)
- 158. 163 Добавочное давление для сферы Для произвольной поверхности плоскости, в которых измеряют радиусы кривизны r1 и
- 159. 163 Смачивание При рассмотрении явлений на границе раздела различных сред нужно рассматривать суммарную поверхностную энергию всех
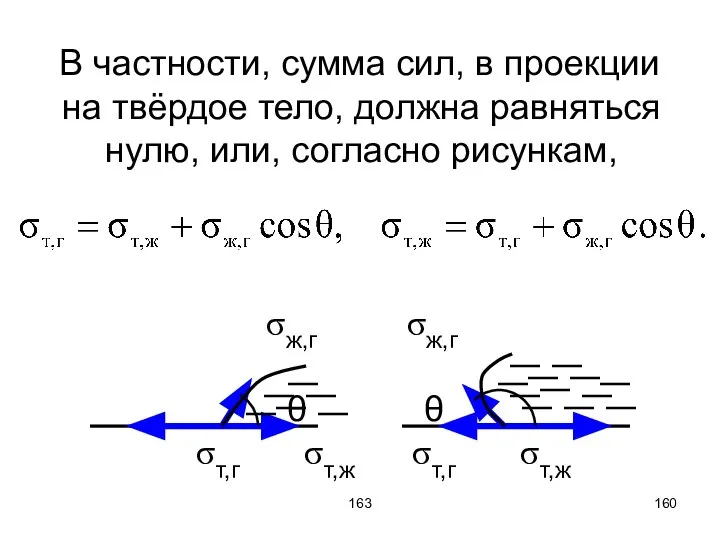
- 160. 163 В частности, сумма сил, в проекции на твёрдое тело, должна равняться нулю, или, согласно рисункам,
- 161. 163 Если σт,г > σж,г + σж,г, то полное смачивание – жидкость неограниченно растекается по поверхности
- 162. 163 Капиллярные явления Капилярные явления – поднятие жидкости (или опускание) на определённую высоту в тонкой трубке
- 164. Скачать презентацию





























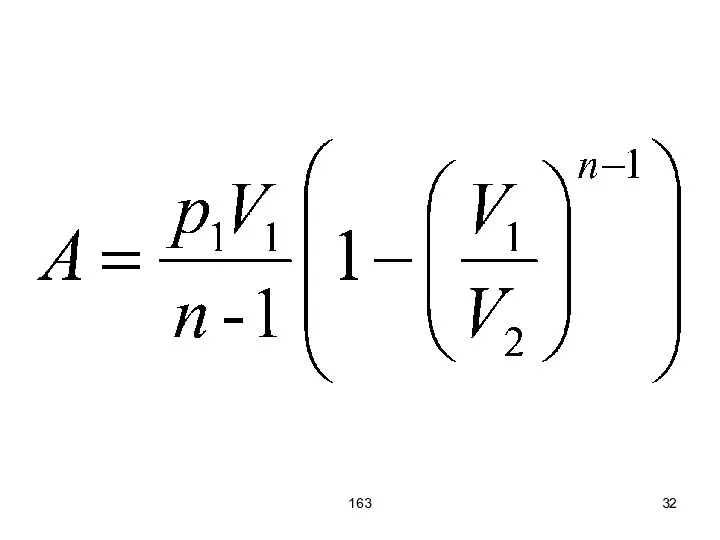










































































































 Двигатель внутреннего сгорания
Двигатель внутреннего сгорания Презентация по физике "Электромагнитные колебания" - скачать __
Презентация по физике "Электромагнитные колебания" - скачать __ Припої. Загальні властивості
Припої. Загальні властивості Спиновая электроника (спинтроника)
Спиновая электроника (спинтроника) Энергия светового поля. Поток энергии в световой волне. Интенсивность света
Энергия светового поля. Поток энергии в световой волне. Интенсивность света Работа в термодинамике.
Работа в термодинамике. Электромагнитные явления. Лекция 3
Электромагнитные явления. Лекция 3 Архитектурная акустика. Основные понятия и определения МСП
Архитектурная акустика. Основные понятия и определения МСП НОВЫЕ ПРЕОБРАЗОВАНИЯ ДЛЯ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
НОВЫЕ ПРЕОБРАЗОВАНИЯ ДЛЯ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ Поляриметрия. Оптически активные вещества, природа оптической активности
Поляриметрия. Оптически активные вещества, природа оптической активности Презентация по физике Линзы. Оптическая сила линзы.
Презентация по физике Линзы. Оптическая сила линзы.  Кінематика поступального та обертального руху
Кінематика поступального та обертального руху Эффект Доплера
Эффект Доплера Метрология как наука. Её значение, цель, задачи, функции
Метрология как наука. Её значение, цель, задачи, функции Электротехника и электроника
Электротехника и электроника Электротехника и электроника. Электрические цепи при импульсном воздействии. (Лекция 12)
Электротехника и электроника. Электрические цепи при импульсном воздействии. (Лекция 12) Физика в нашей жизни
Физика в нашей жизни Электрическое поле. Подготовка к ЕГЭ
Электрическое поле. Подготовка к ЕГЭ Текстура деформации
Текстура деформации Общие теоремы динамики точки
Общие теоремы динамики точки Презентация по физике "Физика как наука" - скачать _
Презентация по физике "Физика как наука" - скачать _ Расчёт массы и объёма тела по его плотности
Расчёт массы и объёма тела по его плотности Неразъемные соединения
Неразъемные соединения Импульс тела. Закон сохранения импульса. Реактивное движение в природе и технике
Импульс тела. Закон сохранения импульса. Реактивное движение в природе и технике Электростатика Электрические взаимодействия (часть 1)
Электростатика Электрические взаимодействия (часть 1) Механика деформируемого твердого тела. Осевые моменты. Момент инерции. Задачи
Механика деформируемого твердого тела. Осевые моменты. Момент инерции. Задачи Методы измерения газопроницаемости
Методы измерения газопроницаемости Фазированные антенные решетки и их назначение. Влияние ФАР на широкополосный сигнал
Фазированные антенные решетки и их назначение. Влияние ФАР на широкополосный сигнал