Содержание
- 2. так как , то т.е. ΔSц.к.= 0 или т.е. S – константа. Это выражение называют равенство
- 3. Таким образом ΔSнеобр > 0 или Это называют – неравенство Клаузиуса. При любом необратимом процессе в
- 4. 5. Второе начало термодинамики Термодинамика, как мы уже поняли, это наука о тепловых процессах, о превращении
- 5. Рассмотрим схему теплового двигателя. От термостата с более высокой температурой Т1, называемого нагревателем за цикл отнимается
- 6. Невозможно создание вечного двигателя Второго рода подтверждается вторым началом термодинамики: 1. Невозможен процесс, единственным результатом которого
- 7. Энтропия замкнутой системы при любых, происходивших в ней процессах, не может убывать (или увеличиваться или оставаться
- 8. 6. Свободная и связанная энергии Как мы только что записали, в обратимом процессе: δA= -(dU -
- 9. Т.е. Аизот=F1–F2, следовательно, свободная энергия есть та работа, которая могло бы совершить тело в обратимом изотермическом
- 10. В термодинамике есть еще понятие – энергетическая потеря в изолированной системе где Tmin − температура окружающей
- 11. 7. Статистический смысл энтропии Посмотрим на энтропию с другой стороны. Макросостояние – это состояние вещества характе-ризующее
- 12. Состояние макроскопического тела (т. е. тела, образованного огромным количеством молекул) может быть задано с помощью объема,
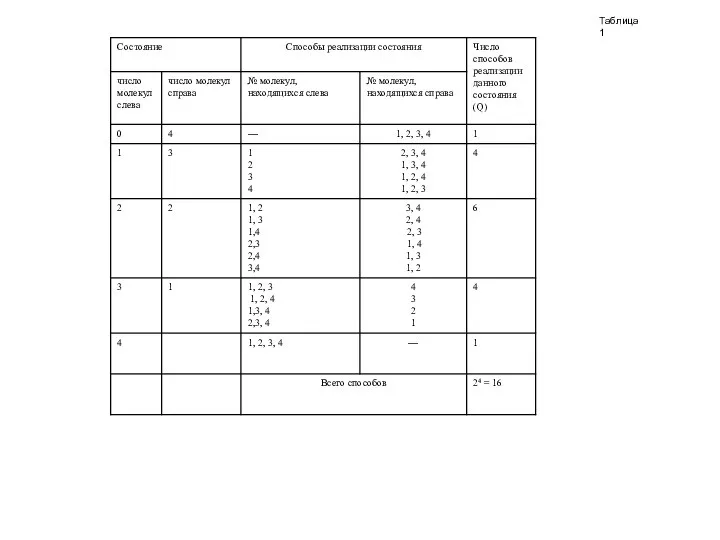
- 13. Начнем со случая, когда полное число молекул равно четырем (рис. 1). Каждая молекула с равной вероятностью
- 14. Таблица 1
- 15. Из рассмотренного примера вытекает, что все микросостояния данной системы равновероятны, вследствие чего статистический вес оказывается пропорциональным
- 16. Домножив и разделив это число на (N-n)!, получим выражение Однако не все z способов приводят к
- 17. (27.2) Легко убедиться в том, что Ω(2,4-2) = 6, а Ω(1,4-1) = 4 (см. табл. 1).
- 18. Случайные отклонения значений какой-либо физической величины х от ее среднего значения называются ф л у к
- 19. Вычислим на основании данных табл. 1 относительную флуктуацию числа молекул в левой половине сосуда. В табл.
- 20. Составив пропорцию, аналогичную (27.7), для N-4 и N=1020, получим относительную флуктуацию (о. ф.) числа молекул в
- 21. Система, находящаяся в равновесном состоянии, время от времени самопроизвольно отклоняется от равновесия. Однако эти отклонения являются
- 28. Термодинамической вероятностью или статисти-ческим весом макросостояния W − называется число макросостояний, которым она может быть осуществлена
- 29. Вероятность сложного события, есть W =W1∙W2, где W1 – первое состояние; W2 – второе состояние. Поэтому
- 30. Например, в ящике черные и белые шары. Они порознь, есть порядок и W невелика. После встряхивания
- 31. На этих рассуждениях Клаузиус в 1877 году и выдвинул гипотезу о тепловой смерти Вселенной (о ней
- 32. 8. Третье начало термодинамики Первое и Второе начало термодинамики не позволяет определить значение энтропии при абсолютном
- 33. Обычно его формулируют следующим образом: энтропия любой равновесной системы при абсолютном нуле температуры может быть равна
- 34. При T = 0, внутренняя энергия и тепловая функция системы прекращают зависеть от температуры, кроме того
- 35. Третье начало термодинамики иногда формулируют следующим способом: при абсолютном нуле температуры любые изменения термодинамической системы происходят
- 36. Следствием Третьего начала является, то что невозможно охладить тело до абсолютного нуля (принцип недостижимости абсолютного нуля
- 37. Лекция 29. Реальные газы Реальные газы Уравнение Ван-дер-Ваальса Изотермы уравнения Ван-дер- Ваальса Внутренняя энергия газа Ван-дер-Ваальса
- 38. 7.1. Реальные газы Как известно, уравнение состояния устанавливает функциональную связь между давлением Р, объемом V, температурой
- 39. Самым простым и известным уравнением состояния является уравнение состояния идеального газа: , где R – универсальная
- 40. Для газов с низкой температурой сжиже-ния (He, H2, Ne и даже N2, O2, Ar, CO, CH4)
- 41. Наибольшее распространение вследствие простоты и физической наглядности получило уравнение Ван-дер-Ваальса (1873). Первая поправка в уравнении состояния
- 42. При понижении температуры межмолекулярное взаимодействие в реальных газах приводит к конденсации (образование жидкости). Межмолекулярное притяжение эквивалентно
- 43. Ван-дер-Ваальс в 1873 г. Дал функциональную интерпретацию внутреннего давления. Согласно модели Ван-дер-Ваальса, силы притяжения между молекулами
- 44. С учетом этих соображений уравнение состояния идеального газа преобразуется в уравнение Ван-дер-Ваальса: , или для одного
- 45. Помимо Нобелевской премии, Ван-дер-Ваальс получил почетную докторскую степень Кембриджского университета. Кроме того, он являлся членом Нидерландской
- 46. Реальные газы – газы, свойства которых зависят от взаимодействия молекул. В обычных условиях, когда средняя потенциальная
- 47. Я.Д. Ван-дер-Ваальс для объяснения свойств реальных газов и жидкостей, предположил, что на малых расстояниях между молекулами
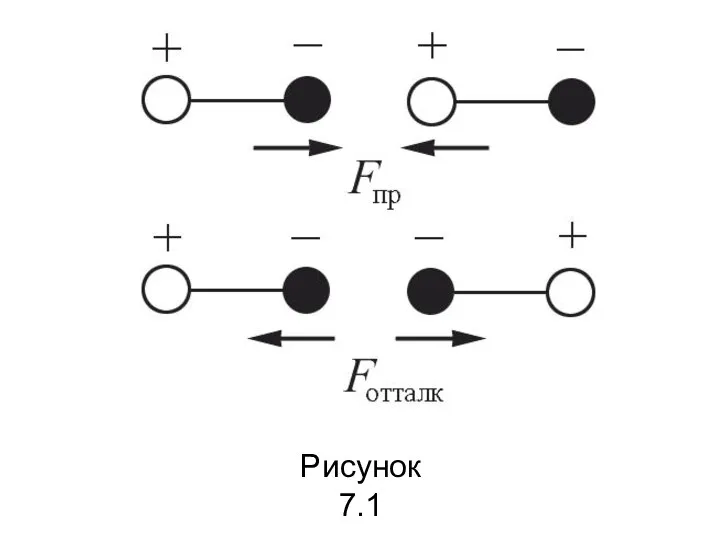
- 48. Ориентационные силы действуют между полярными молекулами – молекулами, обладающими дипольными или квадрупольными моментами. Сила притяжения между
- 49. Рисунок 7.1
- 50. Среднее значение потенциальной энергии ориентационного межмолекулярного взаимодействия равно Uор(r) ~ Р1 Р2 r−6, где p1, p2
- 51. Индукционные (поляризационные) силы действуют между полярной и неполярной молекулами, а также между полярными молекулами. Полярная молекула
- 52. Индукционные силы убывают по тому же закону, что и ориентационные F инд ~ r –7. Дисперсионное
- 53. Данное взаимодействие называется дисперсионным, его энергия определяется поляризуемостью молекул α1, α2: U(r) ~ α1α2 r –6,
- 54. Отметим, что все три силы и энергии одинаковым образом убывают с расстоянием F = Fор +
- 55. Силы отталкивания действуют между молекулами на очень малых расстояниях, когда происходит взаимодействие электронных оболочек атомов, входящих
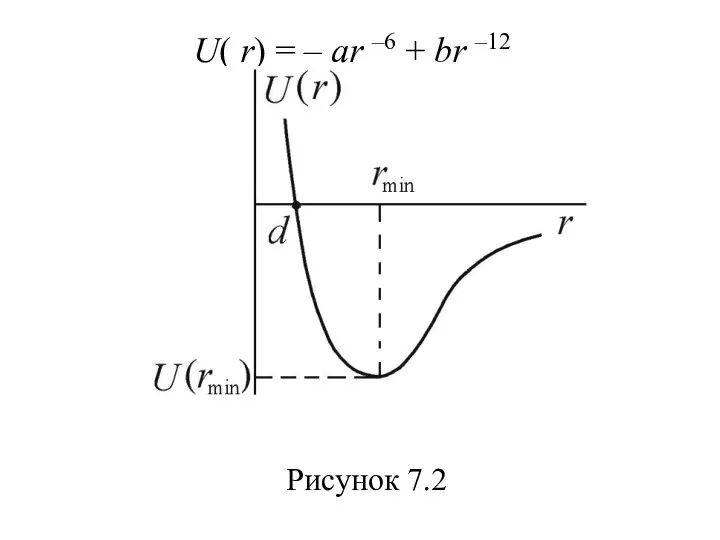
- 56. К хорошему согласию с данными экспериментов приводит допущение, что потенциальная энергия сил отталкивания возрастает с уменьшением
- 57. U( r) = – ar –6 + br –12 Рисунок 7.2
- 58. Глубина потенциала равна U(rmin) = –a2/4b при rmin = (2b/a)1/6 – расстоянии, соответствующем наибольшей энергии связи
- 59. 7.2. Уравнение Ван-дер-Ваальса Уравнение Ван-дер-Ваальса – одно из первых уравнений состояния реального газа, которое было предложено
- 60. Учтем влияние конечных размеров молекул на уравнение состояния реального газа. Давление определяется средней кинетической энергией теплового
- 61. В результате в сосуде, содержащем N молекул конечных размеров, область объемом (N/2)4π(2r)3/3 = 4NVмолек (Vмолек =
- 62. Объем, доступный точечным молекулам, будет равен V − b, а давление, оказываемое на стенки сосуда, определяется
- 63. Для ν = m/μ молей газа уравнение состояния газа с учетом конечного размера молекул примет вид
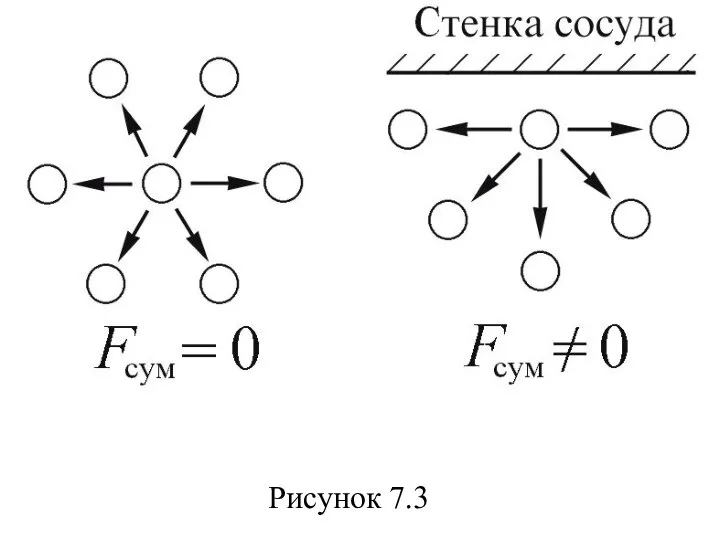
- 64. Рассмотрим теперь влияние сил притяжения на уравнение состояния идеального газа. Будем считать для простоты частицы газа
- 65. Это обусловлено тем, что в то время как в объеме газа действие сил притяжения между молекулами
- 66. Рисунок 7.3
- 67. Дополнительное внутреннее давление пропорционально числу частиц, приходящихся на единицу площади границы nS и силе взаимодействия этих
- 68. В результате избыточное внутреннее давление Pi (i − intrinsic) будет пропорционально квадрату концентрации числа частиц Pi
- 69. С учетом внутреннего давления уравнение состояния примет вид P + Pi = nkT. Причем давление Pi
- 70. Полученное уравнение с учетом выражения для Pi переходит в новое уравнение состояния реального газа при наличии
- 71. Данное уравнение справедливо при условии νb
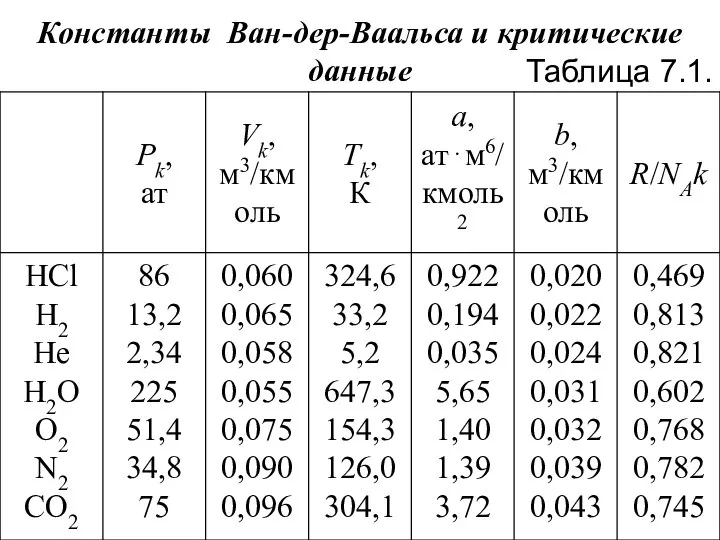
- 72. Константы Ван-дер-Ваальса и критические данные Таблица 7.1.
- 73. Примечание. Константы а и b выбраны таким образом, чтобы получить оптимальное согласование уравнения Ван-дер-Ваальса с измеренными
- 74. 7.3. Изотермы уравнения Ван-дер-Ваальса Проанализируем изотермы уравнения Ван-дер-Ваальса – зависимости Р от V для реального газа
- 75. Поскольку данное уравнение имеет третью степень относительно V, а коэффициенты при V действительны, то оно имеет
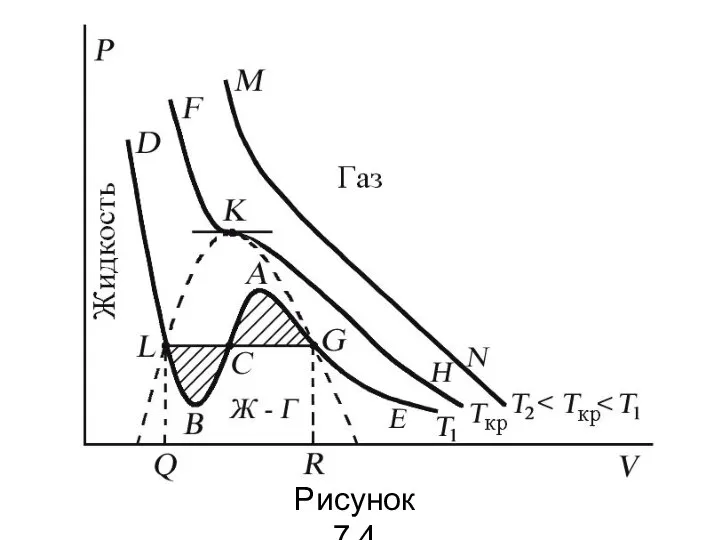
- 76. Рисунок 7.4
- 77. Изотерма при Ткр, которая разделяет немонотонные T Tкр изотермы, соответствует изотерме при критической температуре. При температуре
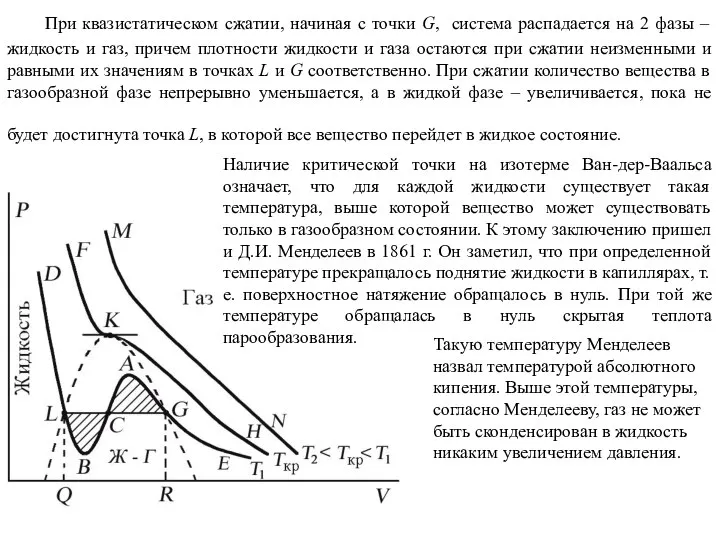
- 78. При температуре газа ниже критической такая однозначность исчезает, а это означает возможность перехода вещества из газообразного
- 79. При квазистатическом сжатии, начиная с точки G, система распадается на 2 фазы – жидкость и газ,
- 80. Критическую точку K мы определили как точку перегиба критической изотермы, в которой касательная к изотерме горизонтальна
- 81. 7.4. Внутренняя энергия газа Ван-дер-Ваальса Энергия одного моля газа Ван-дер-Ваальса слагается из внутренней энергии молекул, составляющих
- 82. Потенциальная энергия притяжения молекул равна работе, необходимой для разведения молекул на бесконечное расстояние друг от друга.
- 83. Знак «минус» указывает на то, что между молекулами действуют силы притяжения; Vm – молярный объем, Vm
- 84. Принципиальное значение уравнения Ван-дер-Ваальса определяется следующими обстоятельствами: 1) уравнение было получено из модельных представлений о свойствах
- 85. Причиной недостаточной точности уравнения Ван-дер-Ваальс считал ассоциацию молекул в газовой фазе, которую не удается описать, учитывая
- 87. Скачать презентацию













































































 Столкновения Абсолютно упругий удар
Столкновения Абсолютно упругий удар  Базовая электрика. Основы
Базовая электрика. Основы Тема 3: ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ 3.1. ЭНЕРГИЯ И ЭНТРОПИЯ Второй закон устанавливает, что самопроизвольные процессы возможн
Тема 3: ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ 3.1. ЭНЕРГИЯ И ЭНТРОПИЯ Второй закон устанавливает, что самопроизвольные процессы возможн Спектроскопия органических соединений
Спектроскопия органических соединений Соединение проводников
Соединение проводников Динамика судна. Общие понятия гидромеханики
Динамика судна. Общие понятия гидромеханики Прямолинейное и криволинейное движение. Движение тела по окружности
Прямолинейное и криволинейное движение. Движение тела по окружности Управління потоками реактивної енергії (вибір потужності компенсуючих установок та їх розміщення у системі електропостачання)
Управління потоками реактивної енергії (вибір потужності компенсуючих установок та їх розміщення у системі електропостачання) « МОУ Липковская Средняя Школа №3» Презентация на тему: « Диффузия» ПОДГОТОВИЛИ: НИКИТИНА НАДЕЖДА И ХАЛИМОВА ЕКАТЕРИНА
« МОУ Липковская Средняя Школа №3» Презентация на тему: « Диффузия» ПОДГОТОВИЛИ: НИКИТИНА НАДЕЖДА И ХАЛИМОВА ЕКАТЕРИНА Электр тізбектеріндегі өтпелі үрдістер
Электр тізбектеріндегі өтпелі үрдістер Законы постоянного тока
Законы постоянного тока Плавление тел
Плавление тел Сила трения
Сила трения Лазер. Области применения лазеров
Лазер. Области применения лазеров Arduino. Электрическая схема
Arduino. Электрическая схема Задачи по физике
Задачи по физике харчування під час радіоактивної небезпеки Підготувала учениця 302 групи Авіакосмічного ліцею ім.І.Сікорського НАУ Гріднєва А
харчування під час радіоактивної небезпеки Підготувала учениця 302 групи Авіакосмічного ліцею ім.І.Сікорського НАУ Гріднєва А Методы травления материалов электронной техники
Методы травления материалов электронной техники Электрические цепи постоянного тока
Электрические цепи постоянного тока Энергетические ресурсы Мирового океана
Энергетические ресурсы Мирового океана Макс Планк Презентация по физике ученицы 12а класса Рижской Гризинькалнской средней шк. им. И. Г. Гердера Максимовой Татьяны
Макс Планк Презентация по физике ученицы 12а класса Рижской Гризинькалнской средней шк. им. И. Г. Гердера Максимовой Татьяны  Уравнение адиабатического процесса для идеального газа
Уравнение адиабатического процесса для идеального газа Закон Архимеда
Закон Архимеда Турбины ТЭС и АЭС. Теория теплового процесса. Основные уравнения теории
Турбины ТЭС и АЭС. Теория теплового процесса. Основные уравнения теории Вес тела
Вес тела Парообразование. Конденсация
Парообразование. Конденсация Презентация по физике "Физика-наука о природе" - скачать
Презентация по физике "Физика-наука о природе" - скачать  Презентация по физике на тему «Производство электроэнергии. Передача электроэнергии на расстоянии.» Ученицы 9 класса «В» Зениной
Презентация по физике на тему «Производство электроэнергии. Передача электроэнергии на расстоянии.» Ученицы 9 класса «В» Зениной