Содержание
- 2. Задача: найти амплитуду А и разность фаз φ между смещением вынужденных колебаний и вынуждаю-щей силой. Воспользуемся
- 3. Каждое слагаемое этого уравнения можно представить в виде соответствующего вращающегося вектора амплитуды: A1 = ω2 –
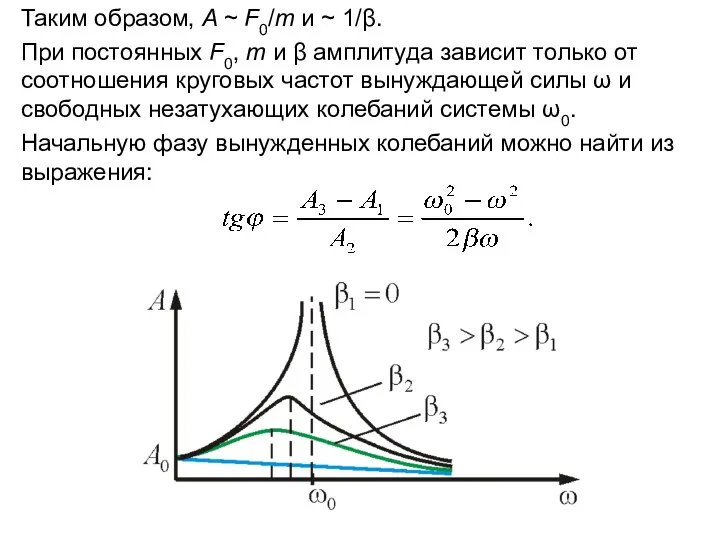
- 4. Таким образом, A ~ F0/m и ~ 1/β. При постоянных F0, m и β амплитуда зависит
- 7. г) физический маятник Физический маятник – твердое тело, которое может совершать колебания под действием собственной силы
- 8. Сравнивая с уравнением свободных незатухающих гармонических колебаний: d2x/dt2 + ω2x = 0 , имеем для физического
- 9. Свободные гармонические колебания в электрическом колебательном контуре Простейшим колебательным контуром является замкнутая цепь, состоящая из емкости
- 10. Сложение гармонических колебаний. Фигуры Лиссажу Сложение колебаний – нахождение значения результирующих ко-лебаний системы при ее участии
- 11. Когерентными называются колебания, разность фаз которых во времени постоянна; т.к. Φ(t) = (ω2 − ω1)t +
- 12. [2ωt >>Δω; cos(-Δωt)=cos(Δωt)] Косинус берется по модулю, так как функция четная и поэтому частота биений ωб
- 14. Скачать презентацию









![[2ωt >>Δω; cos(-Δωt)=cos(Δωt)] Косинус берется по модулю, так как функция четная](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1468980/slide-11.jpg)
 Колебания и волны. Гармонические колебания
Колебания и волны. Гармонические колебания Качественная модель и результаты расчета коэффициента отражения
Качественная модель и результаты расчета коэффициента отражения Основы радиационных и плазменных технологий обработки материалов. Введение
Основы радиационных и плазменных технологий обработки материалов. Введение Механические свойства твердых тел. Виды деформаций
Механические свойства твердых тел. Виды деформаций Магнитный поток. Решение задач
Магнитный поток. Решение задач Магнитные цепи
Магнитные цепи Пространственная система сил
Пространственная система сил Многоповерхностная теория пластичности с одной активной поверхностью
Многоповерхностная теория пластичности с одной активной поверхностью Модельный ряд двигателей ЗМЗ
Модельный ряд двигателей ЗМЗ Механические волны. Звуковая волна
Механические волны. Звуковая волна Равновесие твердых тел
Равновесие твердых тел Количественный хроматографический анализ
Количественный хроматографический анализ Электрический ток в вакууме
Электрический ток в вакууме Технические и технологические характеристики подводного нефтепровода. Практическое занятие 1
Технические и технологические характеристики подводного нефтепровода. Практическое занятие 1 Управление ядерным реактором
Управление ядерным реактором Аттестационная работа. Проектно – исследовательская деятельность на уроках физики «Научное общество школьников»
Аттестационная работа. Проектно – исследовательская деятельность на уроках физики «Научное общество школьников» Методы электрофизической и электрохимической обработки поверхностей заготовок
Методы электрофизической и электрохимической обработки поверхностей заготовок Силовые привод. Характеристика силовых приводов
Силовые привод. Характеристика силовых приводов ІЧ - Спектроскопія. Історія ІЧ-випромінювання
ІЧ - Спектроскопія. Історія ІЧ-випромінювання Примеры выполнения графических работ в курсовой работе по машиностроению
Примеры выполнения графических работ в курсовой работе по машиностроению Презентация по физике "Динамика Законы Ньютона" - скачать
Презентация по физике "Динамика Законы Ньютона" - скачать  Рентгеновские спектры. Закон Мозли
Рентгеновские спектры. Закон Мозли Тензорезистивные датчики
Тензорезистивные датчики Аналитические методы в геохимии
Аналитические методы в геохимии Решение экзаменационных задач по МОАНИ
Решение экзаменационных задач по МОАНИ Доклад: : Животные Красной книги Челябинской области Европейская норка. Привалова Сергея 1 «а»
Доклад: : Животные Красной книги Челябинской области Европейская норка. Привалова Сергея 1 «а»  Нелинейная физика. Турбулентность. Солитоны. Хаос. Странные аттракторы
Нелинейная физика. Турбулентность. Солитоны. Хаос. Странные аттракторы Линзы. Построение изображений в линзах
Линзы. Построение изображений в линзах