Содержание
- 2. Динамическое программирование – это процесс пошагового решения задач, когда на каждом шаге из множества допустимых решений
- 3. Динамическое программирование применимо для задач, обладающих следующими свойствами: Свойство оптимальности для подзадач. Наличие перекрывающихся подзадач.
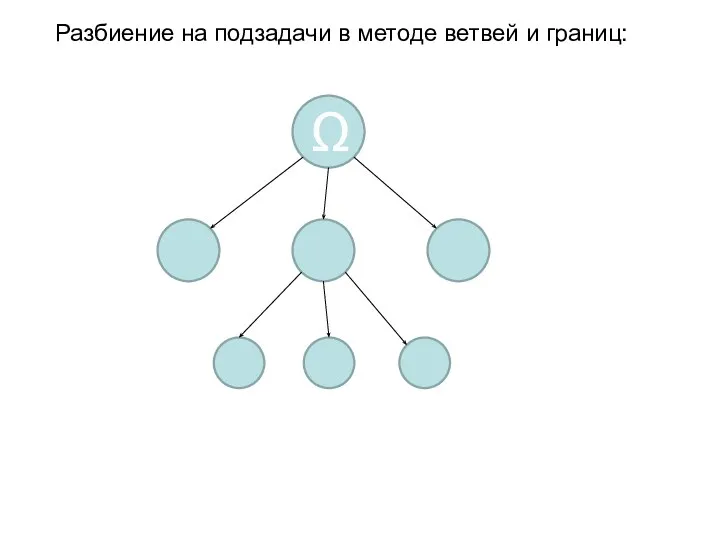
- 4. Разбиение на подзадачи в методе ветвей и границ: Ω
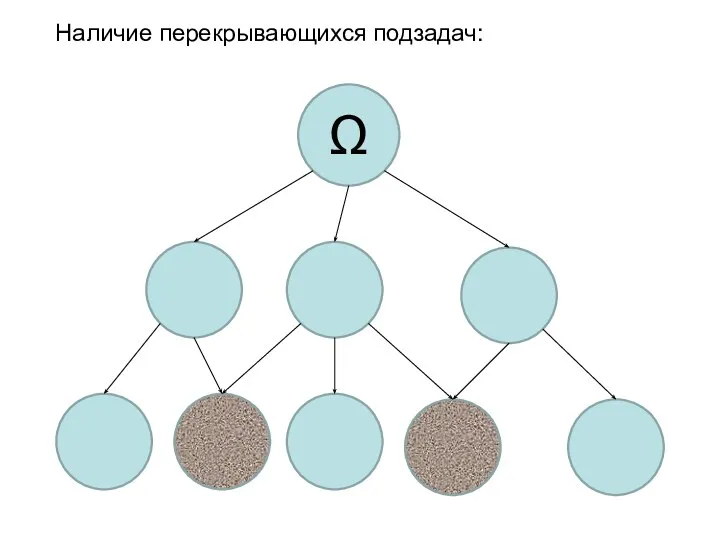
- 5. Наличие перекрывающихся подзадач: Ω
- 6. При использовании динамического программирования каждая из подзадач решается только один раз и ее решение запоминается в
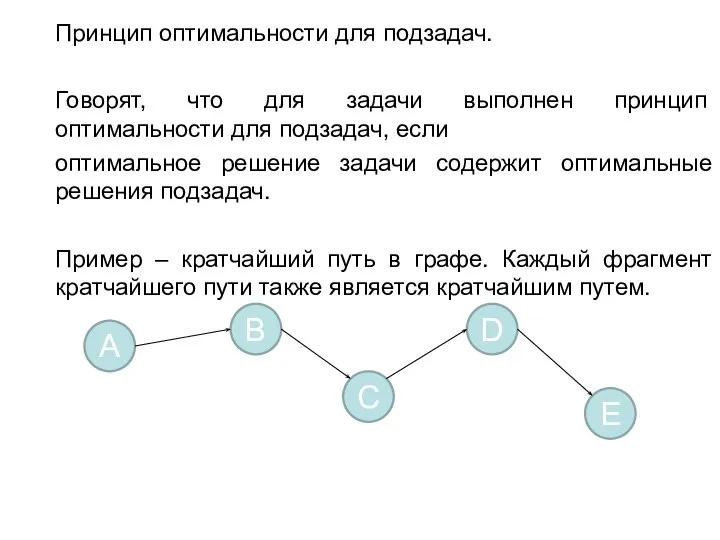
- 7. Принцип оптимальности для подзадач. Говорят, что для задачи выполнен принцип оптимальности для подзадач, если оптимальное решение
- 8. Задача о перемножении матриц. Дано n матриц M1, M2, …, Mn Матрица Mi имеет размеры pi-1
- 9. Пример: M1 10 x 100 M2 100 x 5 M3 5 x 50 ((M1 M2) M3)
- 10. Обозначим Mi...j = MiMi+1…Mj Mi...j = (Mi…Mk)*(Mk+1…Mj) для некоторого i fij – минимальное число операций для
- 11. Псевдокод алгоритма: for i = 1 to n do fii = 0 i = 1, j
- 12. Перемножение матриц: MULT (i, j) if j > i then X = MULT (i, gij) Y
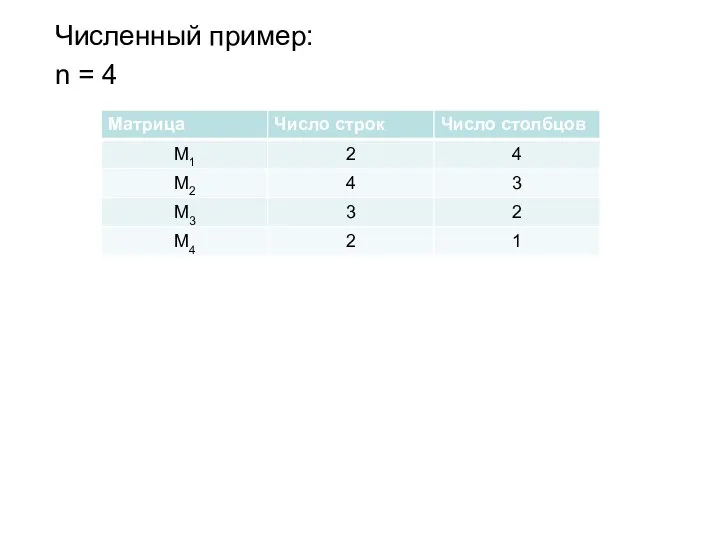
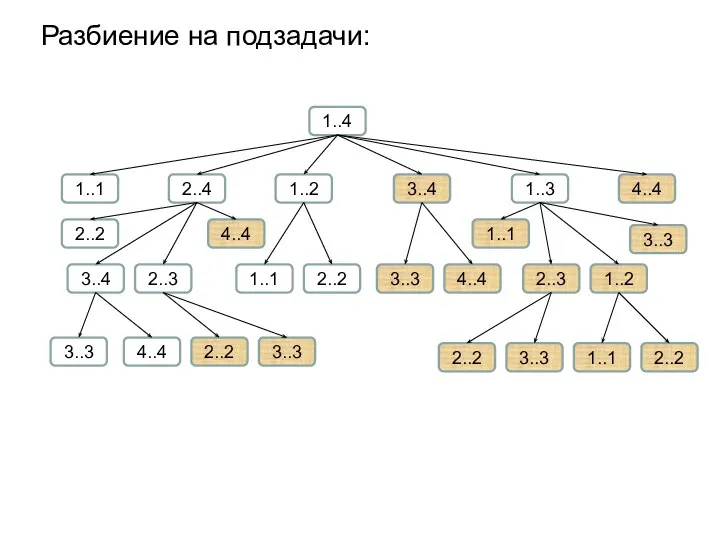
- 13. Численный пример: n = 4
- 14. Разбиение на подзадачи: 1..4 1..1 2..4 1..2 3..4 1..3 4..4 2..2 3..4 2..3 4..4 1..1 2..2
- 16. Скачать презентацию








 Компьютерная память 8 класс - презентации по Информатике
Компьютерная память 8 класс - презентации по Информатике Логическое программирование
Логическое программирование Методы и приемы обеспечения информационной безопасности
Методы и приемы обеспечения информационной безопасности Этапы разработки сайта. Лекция_9
Этапы разработки сайта. Лекция_9 Buying a computer
Buying a computer Создание сайта на Google
Создание сайта на Google Исключения. Методы обработки исключений
Исключения. Методы обработки исключений Модели надежности ПС. Тема 10
Модели надежности ПС. Тема 10 Библиографическое описание документов
Библиографическое описание документов Предмет: информатика Класс: 10-11 Тема урока: Оптимизационное моделирование в электронных таблицах Excel 2007 Крячко София Викторовна У
Предмет: информатика Класс: 10-11 Тема урока: Оптимизационное моделирование в электронных таблицах Excel 2007 Крячко София Викторовна У Разработка электронной обучающей системы по использованию графической среды Unreal Engin 4
Разработка электронной обучающей системы по использованию графической среды Unreal Engin 4 Эталонная модель взаимодействия открытых систем
Эталонная модель взаимодействия открытых систем Анимация в JavaScript
Анимация в JavaScript Настойка ISO для фотокамер CANON
Настойка ISO для фотокамер CANON Презентация "Компьютерная графика" - скачать презентации по Информатике
Презентация "Компьютерная графика" - скачать презентации по Информатике Компоненты Microsoft Office
Компоненты Microsoft Office Введение в информатику
Введение в информатику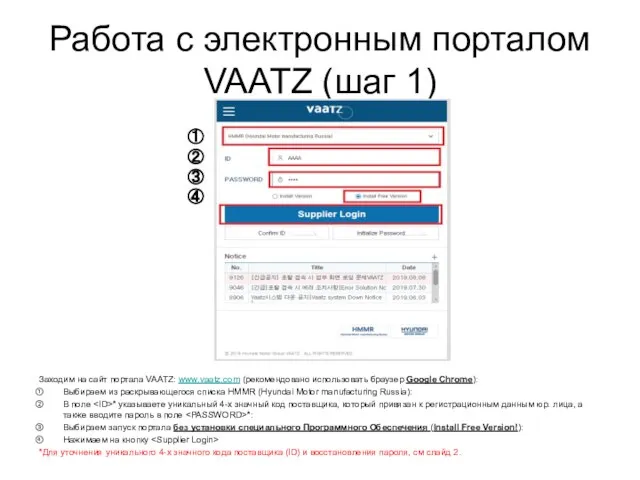 Работа с электронным порталом VAATZ (шаг 1)
Работа с электронным порталом VAATZ (шаг 1) Раздел 7 Линейный анализ устойчивости
Раздел 7 Линейный анализ устойчивости  Оборудование и технологии точного земледелия для эффективного управления производством в агробизнесе
Оборудование и технологии точного земледелия для эффективного управления производством в агробизнесе Общие закономерности работы с системой доступа к информационной системе
Общие закономерности работы с системой доступа к информационной системе Программирование разветвляющихся алгоритмов. Начала программирования
Программирование разветвляющихся алгоритмов. Начала программирования Компьютерные сети
Компьютерные сети Устройства ввода и вывода информации. 8 класс
Устройства ввода и вывода информации. 8 класс Цифровая платформа для испытательных лабораторий
Цифровая платформа для испытательных лабораторий Технологии, применяемые при построении сетей на основе коммутаторов D-Link
Технологии, применяемые при построении сетей на основе коммутаторов D-Link Викторина «Как устроен компьютер?» Автор: Пашкова Е.И. МБОУ СОШ №43 г. Н. Новгород
Викторина «Как устроен компьютер?» Автор: Пашкова Е.И. МБОУ СОШ №43 г. Н. Новгород Kompýuteriň programma üpjünçiligi Operasion sistemanyň ýerine ýetirýän işi
Kompýuteriň programma üpjünçiligi Operasion sistemanyň ýerine ýetirýän işi