Содержание
- 2. Лінійний та нелінійний регресійний аналіз. Побудова лінії регресії. Багатомірний регресійний аналіз.
- 3. Регресійний аналіз Найпростішою формою оцінки стохастичного зв'язку є одновимірний регресійний аналіз, за яким формуються обчислювальні процедури
- 4. Регресія Регресією називають таку криву, вздовж якої розсіювання результатів спостереження мінімальне. Лінійну регресію визначають записом у
- 5. Відтворення функції регресії ідентифікації вигляду регресійної залежності; вибору типу функції регресії ; оцінювання нелінійних регресійних залежностей,
- 6. Початкові умови регресійного аналізу Сумісний розподіл випадкових величин η, ξ має бути нормальним. Дисперсія залежної змінної
- 7. Ідентифікація регресії Метою процедури ідентифікації вигляду регресії є: виявлення наявності зв'язку між X та Y; якщо
- 8. Кореляційні поля
- 9. Лінійний регресійний аналіз Лінійний зв’язок визначається
- 10. Довірче оцінювання емпіричної лінії регресії 1. Обчислення коефіцієнта детермінації R2. 2. Побудова довірчого інтервалу для лінії
- 11. Нелінійний регресійний аналіз У процесі ідентифікації кореляційного поля виявляється, що у багатьох випадках треба відтворювати нелінійну
- 12. Метод найменших квадратів Використовується для відтворення параболічної регресії Де МНК: , де і отримують з
- 13. Метод найменших квадратів Після розв’язку системи отримуємо
- 14. Ортогональні поліноми Чебишева Найпростіша обчислювальна схема відтворення поліноми регресії основана на ортогональних поліномах Чебишева З умови
- 15. Ортогональні поліноми Чебишева Підвищуючи ступінь полінома, для кожної приєднаної функції φк(х) обчислюють коефіцієнт регресії, зберігаючи одержані
- 16. Зведення нелінійний залежностей до лінійних Умовно всі квазілінійні регресійні залежності поділено на чотири групи: До першої
- 17. Зведення нелінійний залежностей до лінійних До третьої групи віднесені теоретичні залежності, які після першого перетворення координат
- 18. Підбір оптимальної лінії регресії Задача в загальному випадку зводиться до побудови декількох ліній регресії та порівнянні
- 19. Множинний аналіз Множинна кореляція Множинний регресійний аналіз
- 20. Множинна кореляція Множинний коефіцієнт кореляції є мірою лінійної залежності між змінною Xi та набором Х1, ...,
- 21. Множинна кореляція У випадку, коли = 1 має місце лінійна залежність, при якій змінна Xt визначається
- 22. Багатовимірний регресійний аналіз Багатовимірний статистичний аналіз визначає причинно-наслідкові зв’язки об’єкта дослідження і його показників (вхідних та
- 23. Багатовимірний регресійний аналіз Задачею регресійного аналізу є дослідження зв’язку між залежними та незалежними величинами Для вирішення
- 25. Скачать презентацию






















 Принтеры (история, принцип работы, характеристика) Автор Семёнов Иван Руководитель Семенова Е.Ю.
Принтеры (история, принцип работы, характеристика) Автор Семёнов Иван Руководитель Семенова Е.Ю. Единое сообщество в социальных сетях «Движение Творца» (на примере соцсети Вконтакте) Основная цель: — создать «узел энергообм
Единое сообщество в социальных сетях «Движение Творца» (на примере соцсети Вконтакте) Основная цель: — создать «узел энергообм Сравнение множеств (2 класс)
Сравнение множеств (2 класс) Протокол BGP
Протокол BGP Графический разделитель
Графический разделитель 3D моделирование и конструирование
3D моделирование и конструирование Графические микропроцессоры
Графические микропроцессоры Презентация "Travel Channel" - скачать презентации по Информатике
Презентация "Travel Channel" - скачать презентации по Информатике Сравнительный анализ совокупной стоимости владения распространенными музыкальными редакторами
Сравнительный анализ совокупной стоимости владения распространенными музыкальными редакторами Архитектура деңгейлері - командалар және деректер жиыны
Архитектура деңгейлері - командалар және деректер жиыны 資訊法律與個資
資訊法律與個資 Основные устройства компьютера
Основные устройства компьютера 1C:ТОИР Управление ремонтами и обслуживанием оборудования (редакция 2,0)
1C:ТОИР Управление ремонтами и обслуживанием оборудования (редакция 2,0) Определения основные понятия свойства множеств. Схема множеств
Определения основные понятия свойства множеств. Схема множеств Многопользовательский доступ к базам данных
Многопользовательский доступ к базам данных Shrink compensation
Shrink compensation Библиотеки мира. (5 класс)
Библиотеки мира. (5 класс) Собственные звуки и рисунки
Собственные звуки и рисунки Создание offline-уроков на основе программы ScreencastOMatic_Setup
Создание offline-уроков на основе программы ScreencastOMatic_Setup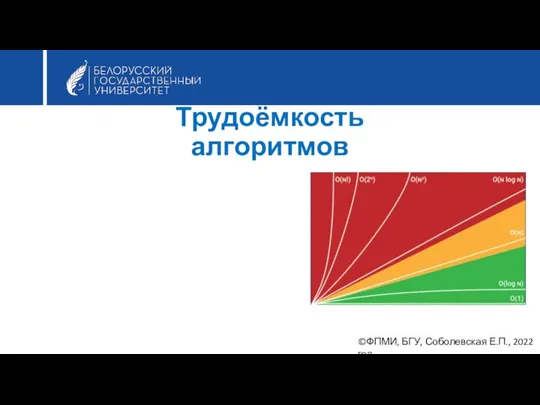 Трудоёмкость алгоритмов
Трудоёмкость алгоритмов Авто в аренду за 5 минут. Ozcar.app
Авто в аренду за 5 минут. Ozcar.app Языки программирования. Java: стоит ли его изучать?
Языки программирования. Java: стоит ли его изучать? Настольные и серверные СУБД. Доступ к данным БД
Настольные и серверные СУБД. Доступ к данным БД Алгоритмы и команда присваивания 9 класс
Алгоритмы и команда присваивания 9 класс  Алгоритмизация и программирование/ лекция 2
Алгоритмизация и программирование/ лекция 2 Activity diagram в контексте языка UML
Activity diagram в контексте языка UML Александр Шаповал Microsoft
Александр Шаповал Microsoft  Использование парсер-комбинаторов на Sprache для построения DSL
Использование парсер-комбинаторов на Sprache для построения DSL