Содержание
- 2. Что такое сложность вычислений? Задачи теории алгоритмов: существует ли алгоритм решения задачи? можно ли им воспользоваться?
- 3. Временнáя сложность T – количество элементарных операций универсального исполнителя (компьютера) Временная сложность алгоритма – функция T(n).
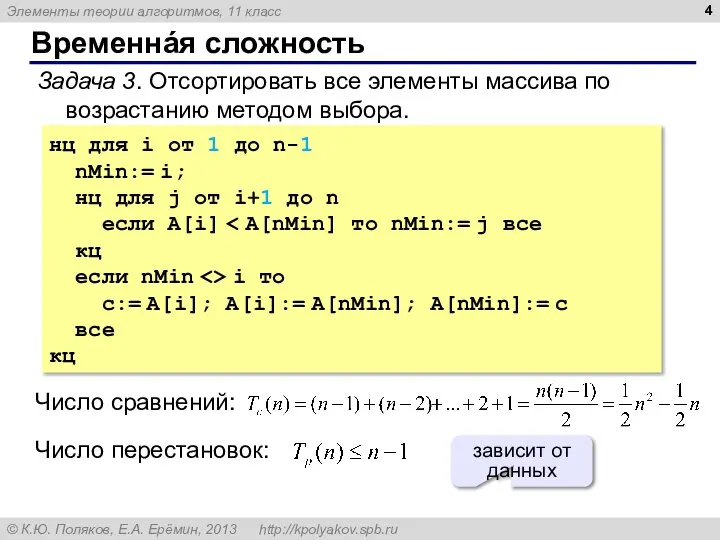
- 4. Временнáя сложность Задача 3. Отсортировать все элементы массива по возрастанию методом выбора. нц для i от
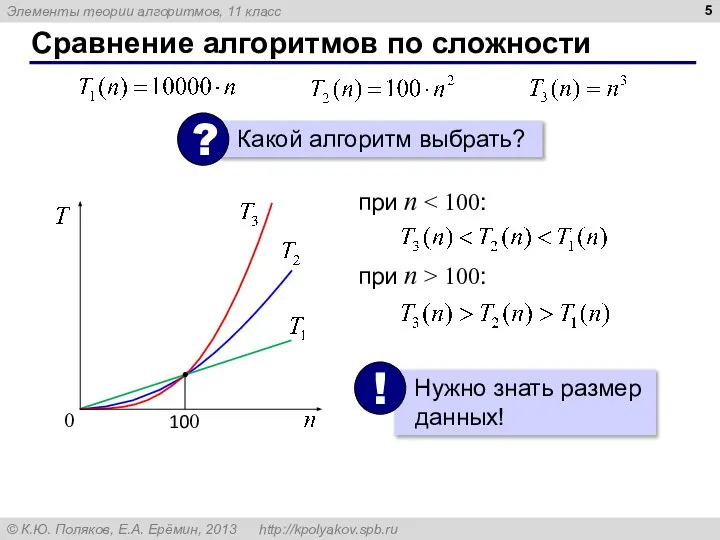
- 5. Сравнение алгоритмов по сложности при n при n > 100:
- 6. Асимптотическая сложность Асимптотическая сложность – это оценка скорости роста количества операций при больших значениях N. сложность
- 7. Асимптотическая сложность сложность O(N3) ⇔ T(N) ≤ c⋅ N3 для N ≥ N0 кубичная сложность O(2N)
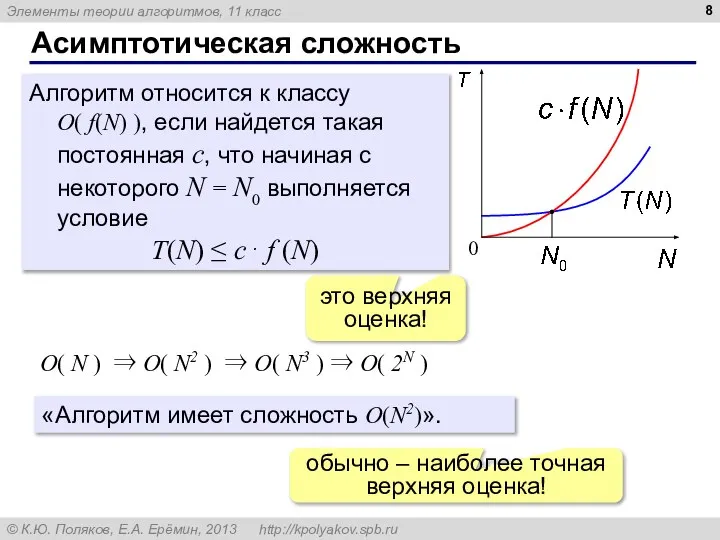
- 8. Асимптотическая сложность Алгоритм относится к классу O( f(N) ), если найдется такая постоянная c, что начиная
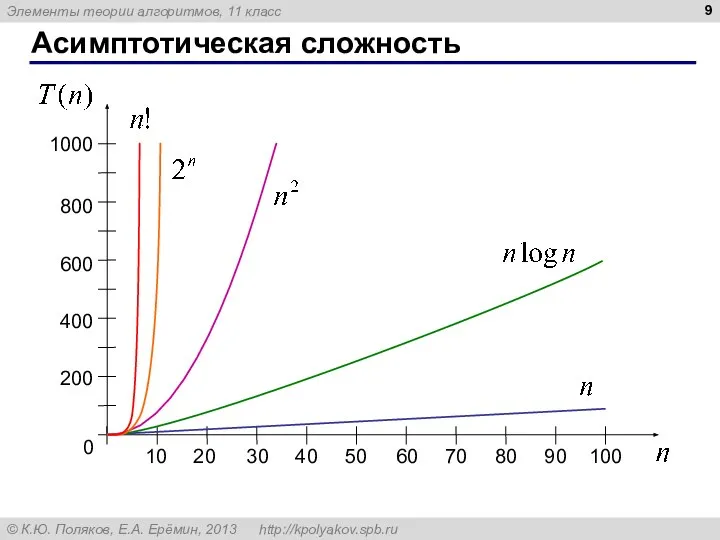
- 9. Асимптотическая сложность
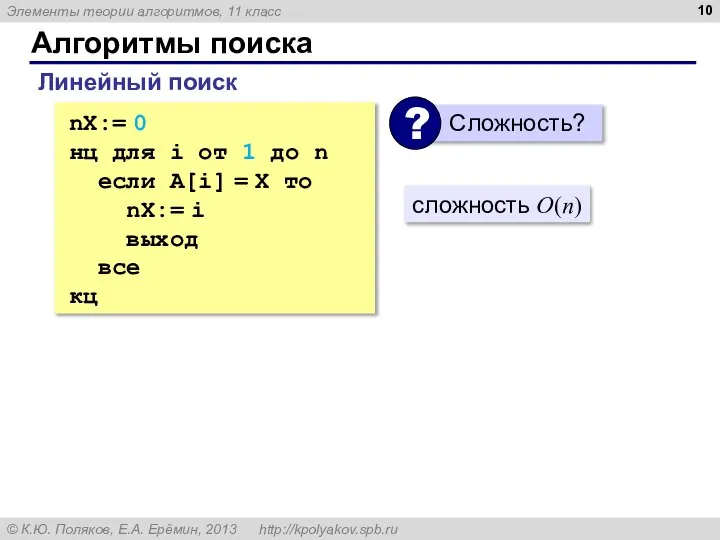
- 10. Алгоритмы поиска Линейный поиск nX:= 0 нц для i от 1 до n если A[i] =
- 11. Алгоритмы поиска Двоичный поиск L:= 1; R:= n + 1 нц пока L c:= div(L +
- 12. Алгоритмы сортировки Метод «пузырька» нц для i от 1 до n-1 нц для j от n-1
- 13. Алгоритмы сортировки Сортировка подсчётом цел C[1:MAX] нц для i от 1 до MAX C[i]:= 0 кц
- 15. Скачать презентацию






![Алгоритмы сортировки Сортировка подсчётом цел C[1:MAX] нц для i от 1](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/661545/slide-12.jpg)
 Технология обработки текстовой информации
Технология обработки текстовой информации  2. Java Spring Core 1. Overview
2. Java Spring Core 1. Overview Обобщение раздела. Коммуникационные технологии
Обобщение раздела. Коммуникационные технологии Запуск программы 3 класс
Запуск программы 3 класс  Образ в шрифте. Шрифт в плакате
Образ в шрифте. Шрифт в плакате Управление задачами
Управление задачами Жизнь без гаджетов
Жизнь без гаджетов Циклы в Паскале. Лабораторная работа
Циклы в Паскале. Лабораторная работа Oturdylan grafikany peýdalanmak
Oturdylan grafikany peýdalanmak Информационное общество. Роль и значение информационных революций. Информатизация как глобальный процесс
Информационное общество. Роль и значение информационных революций. Информатизация как глобальный процесс Сравнительный анализ дизайна интернет-сайтов
Сравнительный анализ дизайна интернет-сайтов Аттестационная работа. Образовательная программа элективного курса Технология создания сайта
Аттестационная работа. Образовательная программа элективного курса Технология создания сайта CSS Grid
CSS Grid Эксплуатация антивирусной защиты ESET NOD32
Эксплуатация антивирусной защиты ESET NOD32 Компьютерные игры – вид нового искусства
Компьютерные игры – вид нового искусства Этапы перевода услуг в электронный вид. Инфраструктура электронного правительства (региональный уровень)
Этапы перевода услуг в электронный вид. Инфраструктура электронного правительства (региональный уровень) Интернет-телеканал #СТУДАК
Интернет-телеканал #СТУДАК Схемы. Многообразие схем
Схемы. Многообразие схем Основы программирования
Основы программирования Аналоговые и цифровые сигналы
Аналоговые и цифровые сигналы Переводчик будущего: нейросеть vs человек
Переводчик будущего: нейросеть vs человек Компас 3D LT
Компас 3D LT Алфавитный подход к определению количества информации
Алфавитный подход к определению количества информации Выполнила: студентка группы Ма1-07 Александрова Д.
Выполнила: студентка группы Ма1-07 Александрова Д. Обобщение по АСУ
Обобщение по АСУ Комп’ютерні віруси та антивірусні програми
Комп’ютерні віруси та антивірусні програми Сортировка, удаление и добавление записей. 9 класс
Сортировка, удаление и добавление записей. 9 класс 3 класс Живая планета
3 класс Живая планета