Содержание
- 2. План лекции Алфавит, кодирование, код Типы кодирования, однозначное декодирование Метод кодирования Хафмана Метод кодирования Фано Элементы
- 3. Алфавитом называется конечное множество символов Сообщением алфавита А называется конечная последовательность символов алфавита А Множество всех
- 4. Кодом называется отображение К : Алф1* —> Алф2*, согласованное с конкатенацией, т.е. удовлетворяющее равенству К(с1с2...сN) =
- 5. Кодированием сообщения называется вычисление кода сообщения Декодированием (дешифровкой) сообщения называется вычисление его прообраза под действием кода
- 6. Алф1 = {a,b,c,d} Алф2 = {0,1} К(а) = 0, К(b) = 01, К(с) = 10, К(d)
- 7. Алф1 = {a,b,c,d} Алф2 = {0,1} К(а) = 0, К(b) = 10, К(с) = 110, К(d)
- 8. Кодовое дерево Кодовым деревом кода К:Алф1 ->Алф2 называется такое дерево Т, с рёбрами помеченными символами из
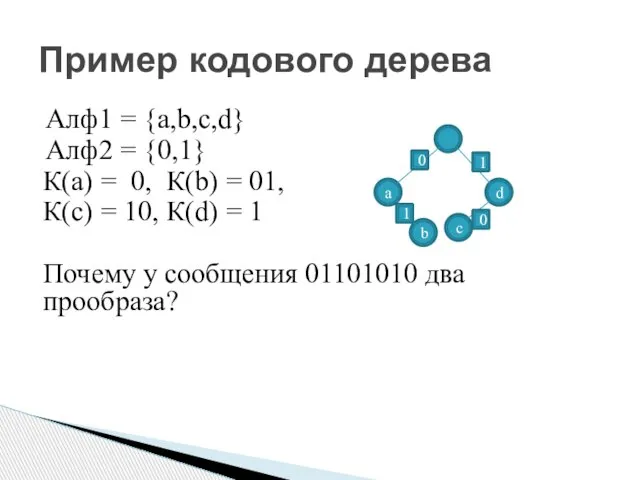
- 9. Пример кодового дерева Алф1 = {a,b,c,d} Алф2 = {0,1} К(а) = 0, К(b) = 01, К(с)
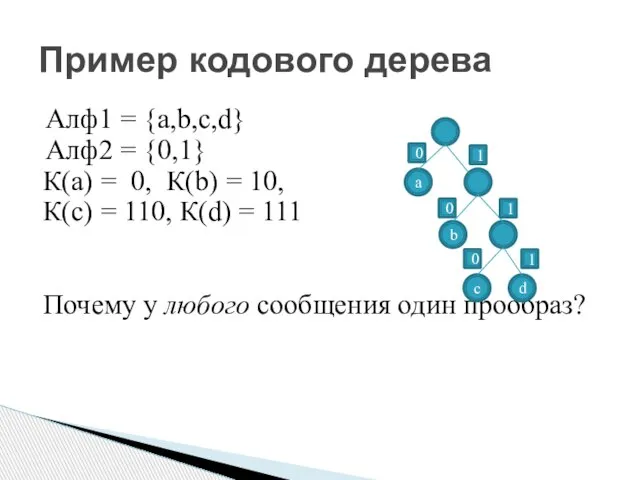
- 10. Пример кодового дерева Алф1 = {a,b,c,d} Алф2 = {0,1} К(а) = 0, К(b) = 10, К(с)
- 11. Префиксный код Код К называется префиксным, если для любых двух сообщений U и V код К(U)
- 12. Примеры префиксных кодов Пример 1 Алф1 = {a,b,c,d} Алф2 = {0,1} К(a) = 00, K(b) =
- 13. Примеры префиксных кодов Пример 2 Алф1 = {a,b,c,d} Алф2 = {0,1} К(а) = 0, К(b) =
- 14. Однозначная декодируемость префиксного кода Теорема Любой префиксный код однозначно декодируем Доказательство Пусть К – префиксный код.
- 15. Алф1 = {a,b,c,d} Алф2 = {0,1} К(a) = 0, К(b) = 101, К(c) = 110, К(d)
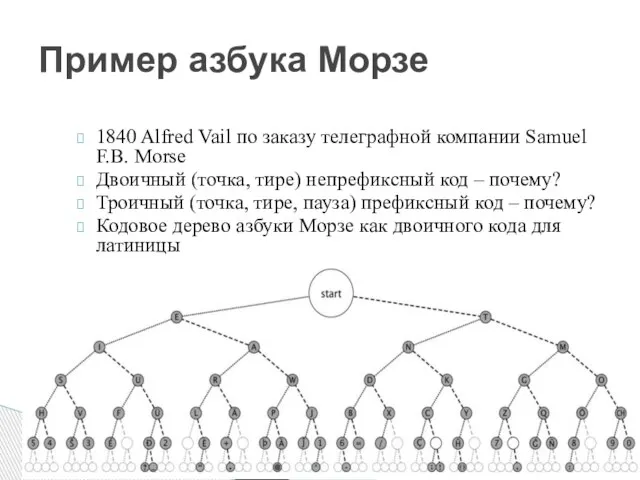
- 16. Пример азбука Морзе 1840 Alfred Vail по заказу телеграфной компании Samuel F.B. Morse Двоичный (точка, тире)
- 17. Понятие оптимального кода Обозначим Δ – множество кодов Алф1* -> Алф2* К – какой-то код из
- 18. Оптимальный двочиный префиксный код Как быстро построить оптимальный двоичный префиксный код для данного сообщения? Использование Сжатие
- 19. Свойства оптимального двоичного префиксного кода Пусть R -- сообщение в алфавите Алф1={c1,…,cn} сx входит в R
- 20. Свойства оптимального двоичного префиксного кода Символов с кодом длины L(K*,сn) (с самым длинным кодом) не менее
- 21. Свойства оптимального двоичного префиксного кода Оптимальный двоичный префиксный код к* для сообщения r, полученного из сообщения
- 22. Построение дерева оптимального префиксного двоичного кода Вход Кратности p1, …, pn вхождений симолов с1, ..., сn
- 23. кол около колокола o – 7; к – 4; л – 4; пробел – 2; a
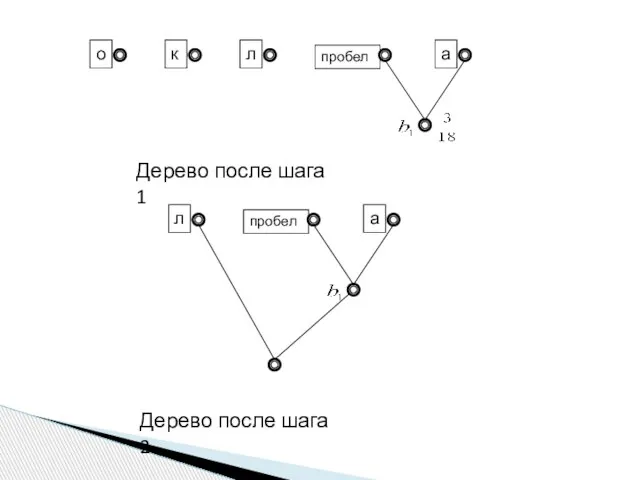
- 24. пробел пробел о к л а Дерево после шага 1 Дерево после шага 2 л а
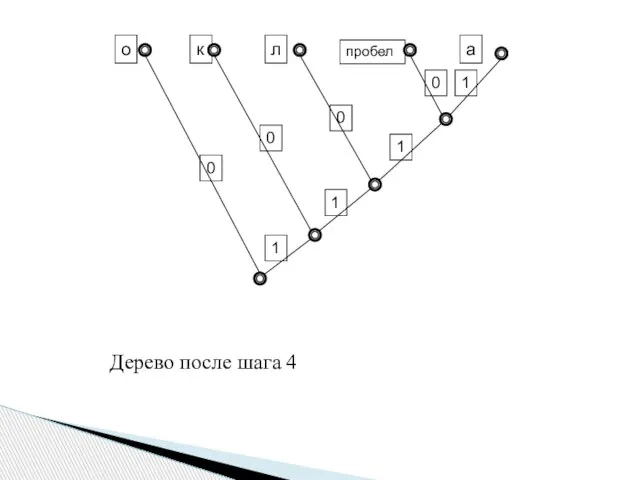
- 25. к пробел 0 0 0 1 1 1 1 Дерево после шага 4 0 о л
- 26. Пример построения кода по кодовому дереву Пометим дуги, исходящие из каждой вершины дерева, единицей и нулем
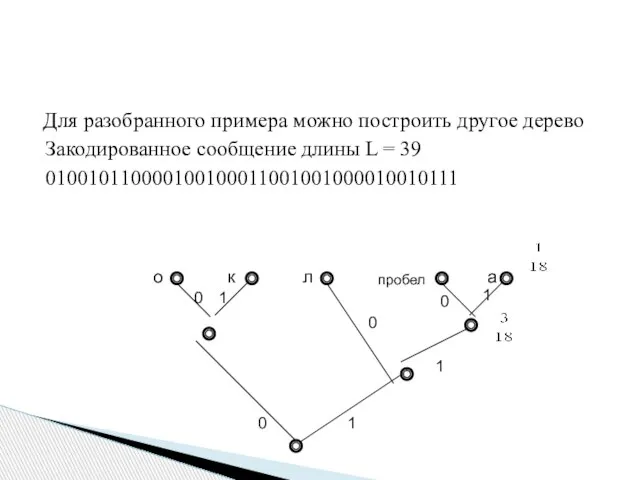
- 27. Для разобранного примера можно построить другое дерево Закодированное сообщение длины L = 39 010010110000100100011001001000010010111
- 28. Теорема Длина кодового слова в оптимальном префиксном двоичном коде ограничена порядковым номером минимального числа Фибоначчи, превосходящего
- 29. Алфавит, кодирование, код Типы кодирования, однозначное декодирование Метод кодирования Хафмана Метод кодирования Фано Элементы теорий вероятностей
- 30. Роберт Марио Фано р. 1917 Один из первых алгоритмов сжатия на основе префиксного кода Метод Фано
- 31. Упорядочим входной алфавит по возрастанию частот p1 Обозначим Sk = p1+p2+…+pk, S0 = 0 Строим таблицу
- 32. K[i][j] заполняем 0 и 1 по след. правилу Для каждого максимального интервала строк [a, b], у
- 33. А = {a, b, c, d, e} Частоты pa = 0.11, pb = 0.15, pc =
- 34. Свойства кода Фано Кодовое дерево для кода Фано обладает следующим свойством Ребра, исходящие из корня, соответствуют
- 35. Свойства кода Фано Код Фано неоптимальный Пример Частоты p1=0.4, p2=p3=p4=p5=0.15 Фано: 00 01 10 110 111
- 36. Клод Шеннон 1916 – 2001, основоположник теории информации Упорядочим входные символы по возрастанию частот и образуем
- 37. nk разложение Sk код p(a) = 0.08 Sa = 0.08 4 0.0001 0001 p(b) = 0.12
- 38. Код Шеннона -- префиксный код Почему? Пусть pk – частота вхождения k-го символа в кодируемое сообщение
- 39. Элементы теории информации Лекция 15
- 40. The Bell System Technical Journal Vol. 27, pp. 379–423, 623–656, July, October, 1948 Имеются источник (кодер)
- 41. Каким должен быть канал, чтобы передать данное сообщение за данное время? За какое время можно передать
- 42. Как измерять пропускную способность канала? Если передача всех символов занимает одинаковое время, то можно использовать символы
- 43. За какое время нельзя передать данное сообщение по данному каналу без потерь? Как понять, что источник
- 44. Как измерить скорость, с которой источник порождает информацию? В процессе передачи сообщения источник "помогает" приемнику выбрать
- 45. Для случая , когда приемник и передатчик знают только частоты отдельных символов p1, p2, …, pn,
- 46. Теорема Все функции, удовлетворяющие условиям 1-3, имеют вид H = - c ∑ pk log(pk) Информационная
- 47. Будем говорить, что источник передал приемнику некоторую информацию о происшедшем событии, на основании которой изменилось представление
- 48. Пример 1 В семье должен родиться ребенок. Пространство элементарных исходов данной случайной величины — {мальчик, девочка},
- 49. log22 = 1 – ? 1 бит соответствует сообщению о том, что произошло одно из двух
- 50. Пример 2 Из колоды вытягивается карта. Пространство элементарных исходов — 52 карты. В отсутствие изначальной информации
- 51. Теорема об аддитивности информации Теорема Количество информации, переносимое сообщением m1 && m2 && … && mN,
- 52. Предположим теперь, что источник является генератором символов из некоторого множества {х1, х2, ...,хn} (назовем его алфавитом
- 53. Рассмотрим теперь модель, в которой элементарным исходом является текстовое сообщение. Таким образом, Ω — это множество
- 54. Понятно, что анализируя различные сообщения, мы будем получать различные экспериментальные частоты символов, но для источников, характеризующихся
- 55. Рассмотрим сообщение m, состоящее из n1 символов x1, n2 символов x2 и т. д. в произвольном
- 56. Количество информации, переносимой сообщением т длины N, определяется как Количество информации, приходящейся в среднем на каждый
- 57. Формула Шеннона Перейдем к пределу по длине всевозможных сообщений (N —> ∞): По формуле (14), вспоминая,
- 58. Формула Хартли Величина I0 (A) характеризует среднее количество информации на один символ из алфавита А с
- 59. Событие, которое может произойти или нет, называют случайным. Примеры: попадание стрелка в мишень, извлечение дамы пик
- 60. Определение Пространство элементарных событий (исходов) Ω – множество всех различных событий, возможных при проведении эксперимента. Элементарность
- 61. Примеры: Будем бросать монету до тех пор, пока не выпадет герб. После этого эксперимент закончим. «Элементарный
- 62. Формула ω∈Ω означает, что элементарное событие ω является элементом пространства Ω. Многие события естественно описывать множествами,
- 63. Определим формально меру события µ, как отображение из пространства Ω в N, обладающее следующими свойствами: 1)
- 64. Введем функцию p(S) вероятности события как численного выражения возможности события S на заданном пространстве элементарных исходов
- 65. Говорят, что заданы вероятности элементарных событий, если на Ω задана неотрицательная числовая функция p такая, что:
- 66. Вероятность того, что при бросании кости выпадет единица, равна Вероятность появления четного числа очков равна Паскаль
- 67. Теорема о сложении вероятностей Если пересечение событий А и В непусто, то р(А U В) =
- 68. Теорема об умножении вероятностей Рассмотрим теперь серию экспериментов, в которой некоторая случайная величина наблюдается последовательно несколько
- 69. Определим формально меру события µ, как отображение из пространства Ω в N, обладающее следующими свойствами:
- 70. КОНЕЦ ЛЕКЦИИ
- 71. Избыточность кодирования Оказывается, что величина I0(А) определяет предел сжимаемости кода: никакой двоичный код не может иметь
- 72. Заметив, что lim N->∞ L/N - есть средняя длина кодового слова K0(A), получим независимое от сообщения
- 73. Посчитаем информационную емкость кода: длина исходного сообщения N = 18, длина кода L = 39 битов.
- 74. Реализация проекта Архиватор должен вызываться из командной строки, формат вызова: harc.exe –[axdlt] arc[.ext] file_1 file_2 …
- 75. Проверка целостности архива _stat, _wstat, _stati64, _wstati64 int _stat(const char* path, struct _stat *buffer); #include CRC32
- 76. Построение дерева Хаффмана Вход: A – исходный набор символов , P= - распределение их частот; –
- 77. Алгоритм: Определить алфавит А = { с1, с2 , ... , сn } сообщения S и
- 78. Критерии качества кодирования: — минимальная длина кода; — однозначное декодирование.
- 80. Скачать презентацию
























![K[i][j] заполняем 0 и 1 по след. правилу Для каждого максимального](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/555713/slide-31.jpg)














































 Элементы алгебры логики (урок 1.4.)
Элементы алгебры логики (урок 1.4.) Конструирование алгоритма. Последовательное построение алгоритма. (Урок 46)
Конструирование алгоритма. Последовательное построение алгоритма. (Урок 46) История латинской раскладки клавиатуры
История латинской раскладки клавиатуры Лекция 2 Delphi
Лекция 2 Delphi  Сравнение множеств (2 класс)
Сравнение множеств (2 класс) Компьютер или подвижная игра? Авторы учащиеся 10 класса.
Компьютер или подвижная игра? Авторы учащиеся 10 класса. Лекции по практике (HTML, CSS, JS, PHP, MySQL)
Лекции по практике (HTML, CSS, JS, PHP, MySQL) Работа с контентом. Шаблон контент-плана
Работа с контентом. Шаблон контент-плана Инженерная графика 10 - 11 класс
Инженерная графика 10 - 11 класс Основополагающие принципы устройства ЭВМ
Основополагающие принципы устройства ЭВМ Проверочная работа 5 класс Информация. Информатика. Компьютер
Проверочная работа 5 класс Информация. Информатика. Компьютер Методика проведения самостоятельной работы по информатике
Методика проведения самостоятельной работы по информатике ccee30e7b89a763a
ccee30e7b89a763a Компьютерные изображения
Компьютерные изображения Безопасный поиск в сети Интернет
Безопасный поиск в сети Интернет Сервисы 1С: ИТС для удобной и эффективной работы без налоговых рисков
Сервисы 1С: ИТС для удобной и эффективной работы без налоговых рисков Разработка сайтов для конкретных предприятий
Разработка сайтов для конкретных предприятий Pipes. Пользовательские директивы
Pipes. Пользовательские директивы Отношения объектов. (5-7 класс)
Отношения объектов. (5-7 класс) Алгоритм
Алгоритм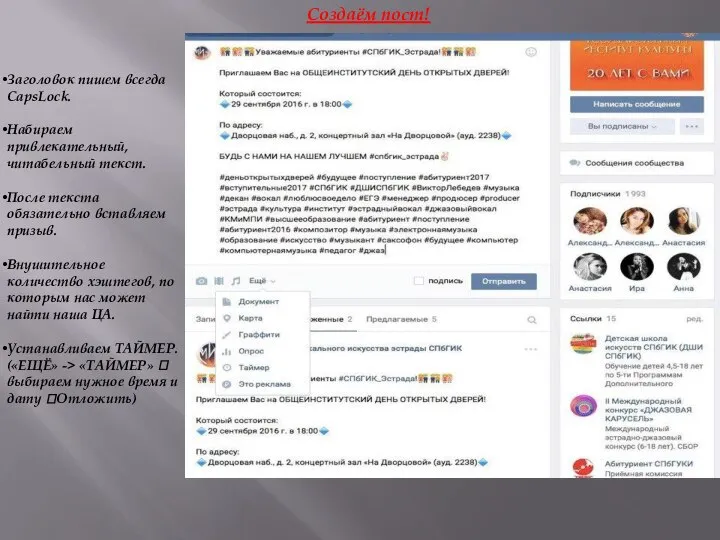 Инструкция по созданию постов
Инструкция по созданию постов Key Management. Cryptography applications
Key Management. Cryptography applications Инструменты фотошоп
Инструменты фотошоп Операционные системы
Операционные системы Формализация понятия алгоритма
Формализация понятия алгоритма Графика в Бейсике Автор: Бауэр Наталья Ивановна, преподаватель информатики и специальных дисциплин ГОУ СПО «Белгородский педаг
Графика в Бейсике Автор: Бауэр Наталья Ивановна, преподаватель информатики и специальных дисциплин ГОУ СПО «Белгородский педаг Что такое Linux
Что такое Linux Требования к компьютерной презентации
Требования к компьютерной презентации