Лекция 3. Применение линейного программирования в математических моделях Содержание лекции: Принцип оптимальности в планировани
Содержание
- 2. /23 Литература Экономико-математические методы и прикладные модели: Учеб. пособие для вузов / Под ред. В.В. Федосеева.
- 3. /23 3.1. Принцип оптимальности в планировании и управлении Принцип оптимальности предполагает следующее: наличие определённых ресурсов наличие
- 4. /23 3.2. Задача линейного программирования Это развёрнутая форма записи Линейная целевая функция Линейные ограни-чения Условия неотрицательности
- 5. /23 3.2. Задача линейного программирования Это каноническая форма записи Линейная целевая функция Линейные ограни-чения Условия неотрицательности
- 6. /23 3.2. Задача линейного программирования Это матричная форма записи Она тождественна канонической форме Линейная целевая функция
- 7. /23 3.2. Задача линейного программирования Это стандартная форма записи Линейная целевая функция Линейные ограни-чения Условия неотрицательности
- 8. /23 3.2. Любой вектор x, удовлетворяющий ограничениям и условиям неотрицательности (безотносительно к целевой функции), называется допустимым
- 9. /23 3.2. ЗЛП может: не иметь ни одного оптимального решения допустимой области не существует – система
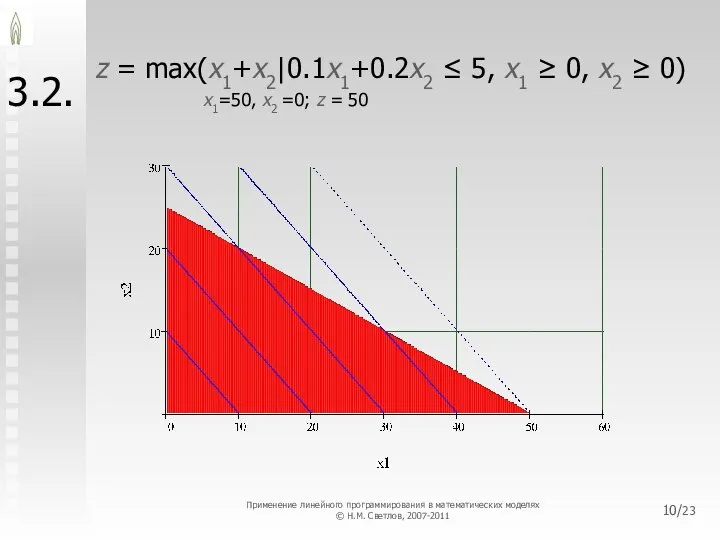
- 10. /23 3.2. z = max(x1+x2|0.1x1+0.2x2 ≤ 5, x1 ≥ 0, x2 ≥ 0) x1=50, x2 =0;
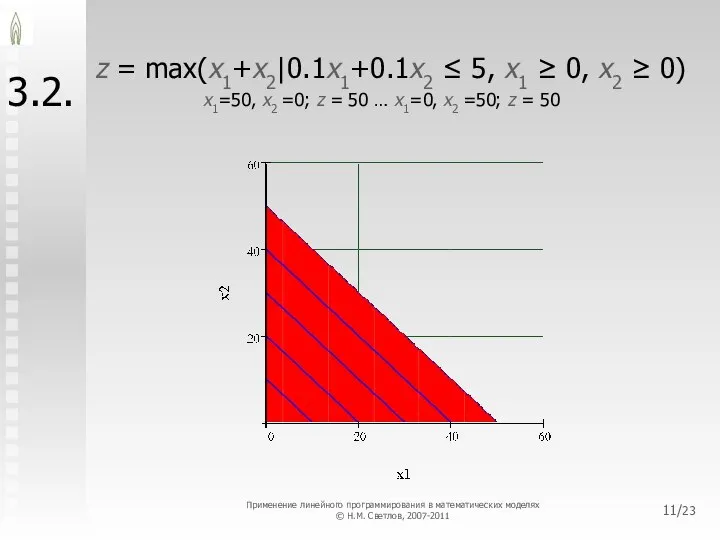
- 11. /23 3.2. z = max(x1+x2|0.1x1+0.1x2 ≤ 5, x1 ≥ 0, x2 ≥ 0) x1=50, x2 =0;
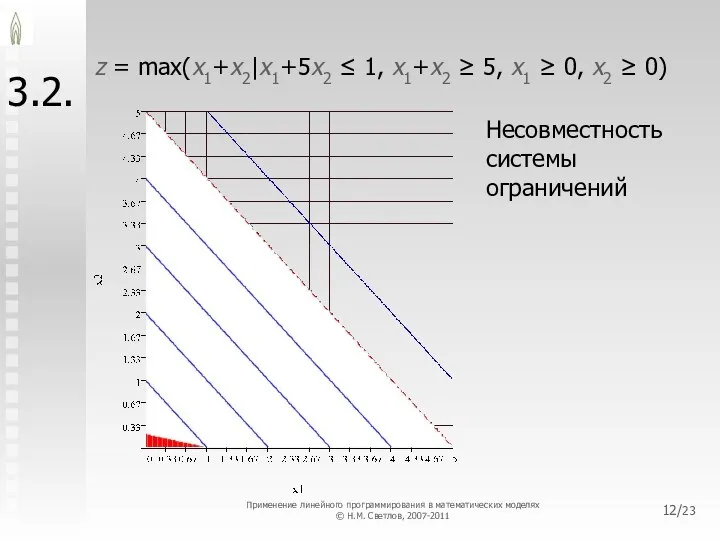
- 12. /23 3.2. z = max(x1+x2|x1+5x2 ≤ 1, x1+x2 ≥ 5, x1 ≥ 0, x2 ≥ 0)
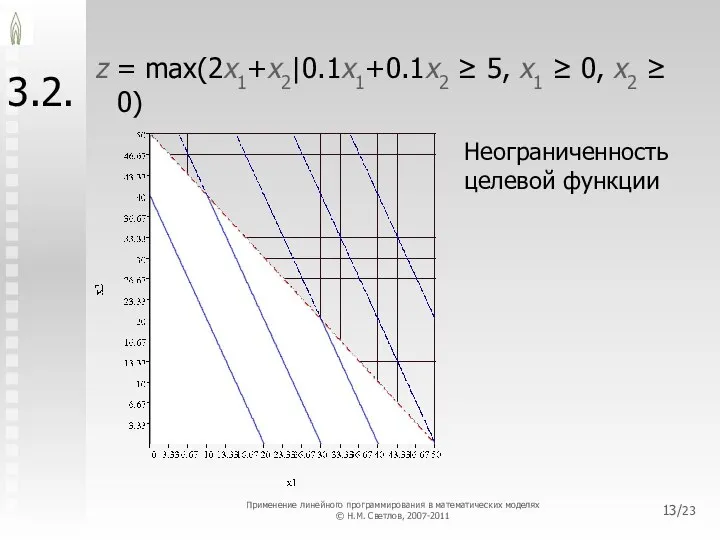
- 13. /23 3.2. z = max(2x1+x2|0.1x1+0.1x2 ≥ 5, x1 ≥ 0, x2 ≥ 0) Неограниченность целевой функции
- 14. /23 3.3. Симплексный метод Исходные условия применения симплексного метода ЗЛП записана в канонической форме Её ограничения
- 15. /23 3.3. z = max(x1+x2|0.1x1+0.2x2 ≤ 5, x1–2x2 ≤ 75, x1 ≥ 0, x2 ≥ 0)
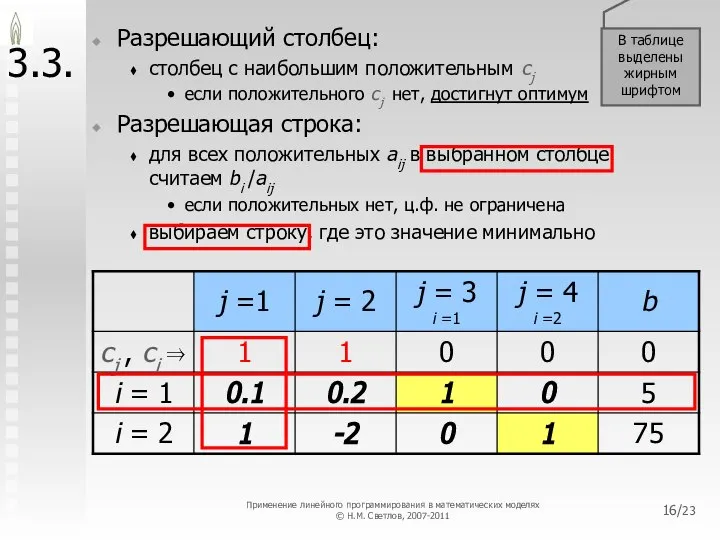
- 16. /23 В таблице выделены жирным шрифтом 3.3. Разрешающий столбец: столбец с наибольшим положительным cj если положительного
- 17. /23 3.3. Выполняем обыкновенные жордановы исключения во всей таблице: для строк i ≠i' : aijнов =
- 18. /23 3.3. Опорное решение может быть получено по следующей процедуре: Выбираем произвольный набор базисных переменных и
- 19. /23 3.3. В некоторых случаях алгоритм симплексного метода может зацикливаться. Пути преодоления этой проблемы описаны в
- 20. /23 3.4. Экономические приложения линейного программирования Матрица потребности в ресурсах для обеспечения единичного объёма производства в
- 21. /23 3.4. Экономические приложения линейного программирования Вектор цен продукции (за вычетом НДС), руб./ед. Вектор цен ресурсов
- 22. Применение линейного программирования в математических моделях (с) Н.М. Светлов, 2007 /23 3.5. Программное обеспечение линейного программирования
- 24. Скачать презентацию















 Составление программы линейной структуры
Составление программы линейной структуры 1
1 Презентация "Кодирование информации: 100" - скачать презентации по Информатике
Презентация "Кодирование информации: 100" - скачать презентации по Информатике Зачисление в ОУ
Зачисление в ОУ Ознакомление с основными этапами разработки ПО, методами проектирования ПО и документирования программных продукто
Ознакомление с основными этапами разработки ПО, методами проектирования ПО и документирования программных продукто Основные теги HTML
Основные теги HTML Цикли з умовою
Цикли з умовою Цикл while. Программирование на языке Python
Цикл while. Программирование на языке Python Компьютерный сленг
Компьютерный сленг Как создать сайт?
Как создать сайт? Презентация "Введение в мультимедийные базы данных" - скачать презентации по Информатике
Презентация "Введение в мультимедийные базы данных" - скачать презентации по Информатике Археографический заголовок
Археографический заголовок Python. Занятие 4
Python. Занятие 4 Аттестационная работа. Образовательная программа внеурочной деятельности по информатике Занимательная компьютерная графика
Аттестационная работа. Образовательная программа внеурочной деятельности по информатике Занимательная компьютерная графика Что изучает предмет ОБЖ
Что изучает предмет ОБЖ 3D files browser
3D files browser Транзакции и блокировки. (Лекция 11)
Транзакции и блокировки. (Лекция 11) Титульный лист
Титульный лист Информатика. Жесткий диск
Информатика. Жесткий диск Создание элементов управления презентацией
Создание элементов управления презентацией Unit 6: Software Design & Development. Data Types in Programming
Unit 6: Software Design & Development. Data Types in Programming Быстрая сортировка (Quicksort). Повторяющиеся ключи. Применение сортировок
Быстрая сортировка (Quicksort). Повторяющиеся ключи. Применение сортировок Деструктивное поведение
Деструктивное поведение Приложение для управления изделием: радиомаяк азимутально-дальномерный, высокомобильный
Приложение для управления изделием: радиомаяк азимутально-дальномерный, высокомобильный Аттестационная работа. Формирование метапредметных результатов обучения на уроках информатики с использованием метода проектов
Аттестационная работа. Формирование метапредметных результатов обучения на уроках информатики с использованием метода проектов Настройка маршрутизаторов DIR-100
Настройка маршрутизаторов DIR-100 Текстовий редактор MS Word 1
Текстовий редактор MS Word 1 Циклические алгоритмы
Циклические алгоритмы