Содержание
- 2. способ представления функции в ДНФ или КНФ с минимальным количеством членов и минимальным набором переменных Преобразование
- 3. Первый этап (получение сокращённой формы)
- 4. Получение сокращённой формы
- 5. Пример Пусть есть таблица истинности
- 6. Результаты упрощения
- 7. Рассмотренный выше пример уже удовлетворяет определению минимальной формы, однако далеко не всегда после первого этапа сокращённая
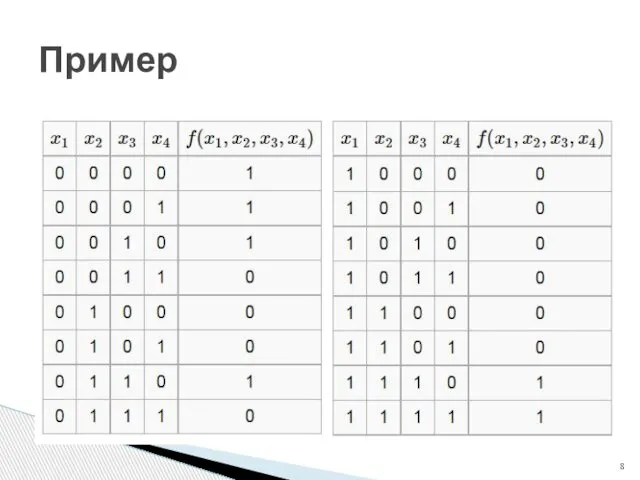
- 8. Пример
- 9. Получение СДНФ
- 10. Мы вновь получили дизъюнкцию простых импликант, на этот раз в количестве пяти штук. Чтобы получить минимальную
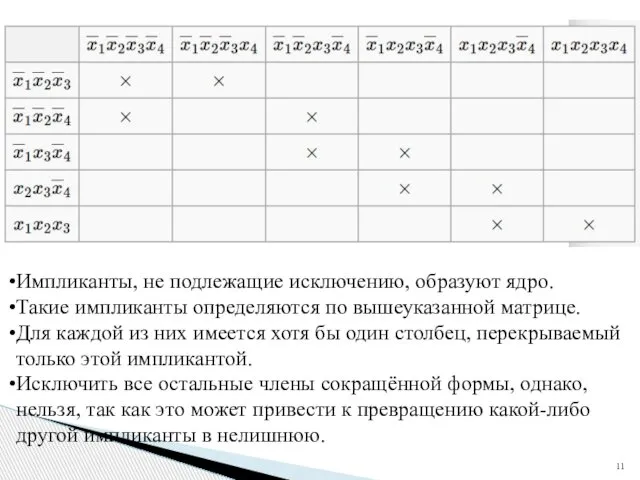
- 11. Импликанты, не подлежащие исключению, образуют ядро. Такие импликанты определяются по вышеуказанной матрице. Для каждой из них
- 12. Выбор остальных импликант, что войдут в минимальную форму, сводится к нахождению минимального набора неядровых импликант, которые
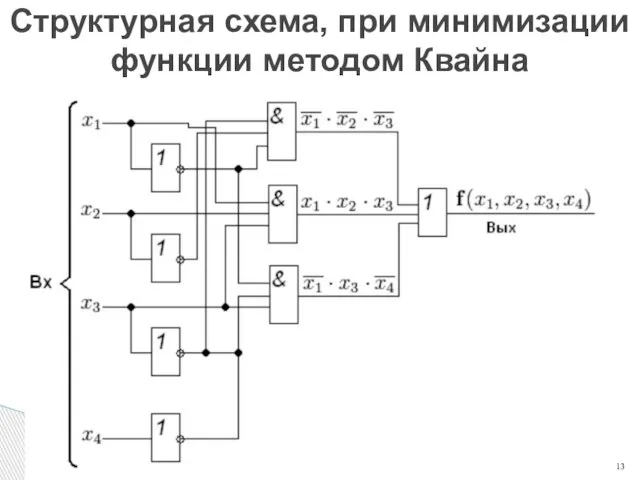
- 13. Структурная схема, при минимизации функции методом Квайна
- 14. Использование метода для получения минимальной КНФ
- 15. Нахождение первичных импликант; Эти импликанты разбиваются на группы, в каждую группу входят импликанты с равным количеством
- 16. Положим, что функция записана в виде СДНФ. Тогда первичными импликантами будут 010~, 0~11, 1~01, 111~, ~1~1.
- 17. Существенными импликантами будут те, где в соответствующих столбцах стоит только одна метка. Без любой из них
- 18. Убираем лишние строки (в данном случае только одну) и выберем такую совокупность первичных импликант, что включает
- 19. Его можно применять на большом количестве переменных в САПР, с использованием ЭВМ для минимизации полностью или
- 20. Затруднительна ручная минимизация функций с шестью и более переменных; Метод Куайна — Мак-Класки алгоритмически неинвариантен: время
- 21. в теории сложности вычислений задача, для решения которой требуется обработка более чем 1093 бит информации. Число
- 22. Сумматор логический операционный узел, выполняющий арифметическое сложение кодов двух чисел. При арифметическом сложении выполняются и другие
- 23. четвертьсумматоры; полусумматоры; полные одноразрядные двоичные сумматоры По числу входов и выходов одноразрядные, многоразрядные. По количеству одновременно
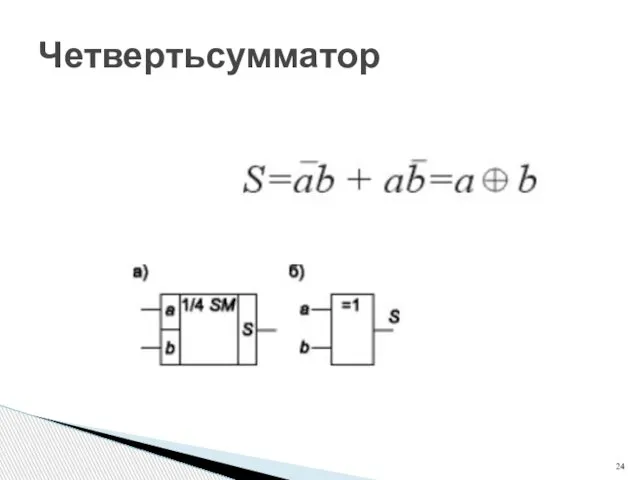
- 24. Четвертьсумматор
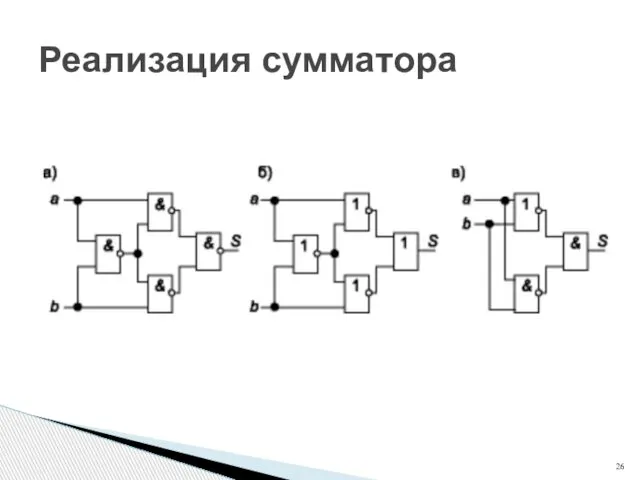
- 25. Реализация сумматора
- 26. Реализация сумматора
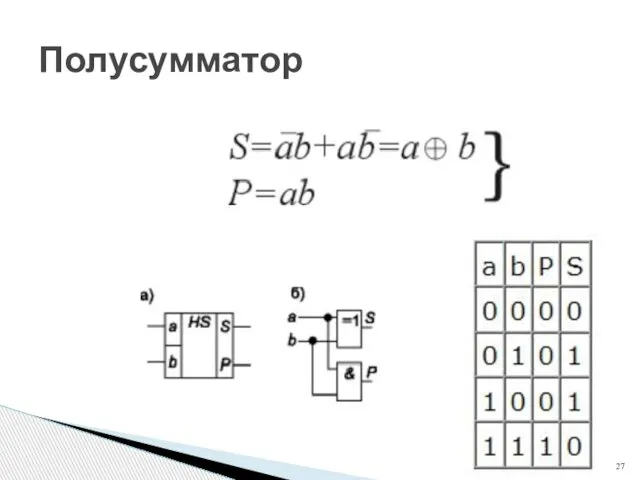
- 27. Полусумматор
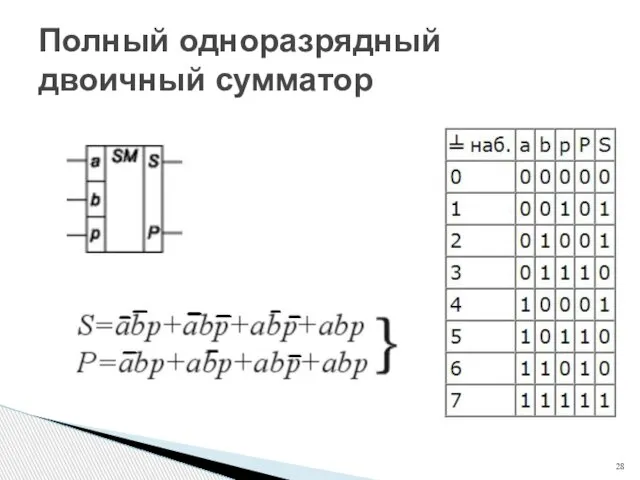
- 28. Полный одноразрядный двоичный сумматор
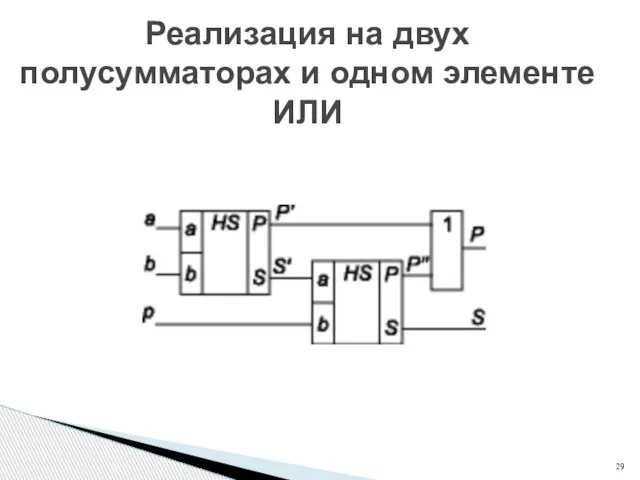
- 29. Реализация на двух полусумматорах и одном элементе ИЛИ
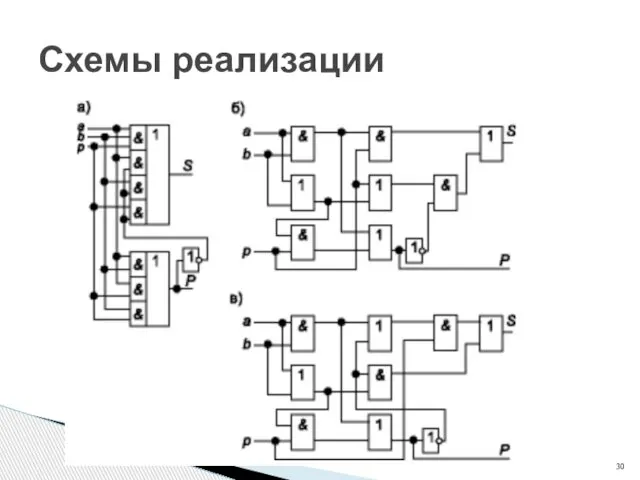
- 30. Схемы реализации
- 31. Полувычитатель
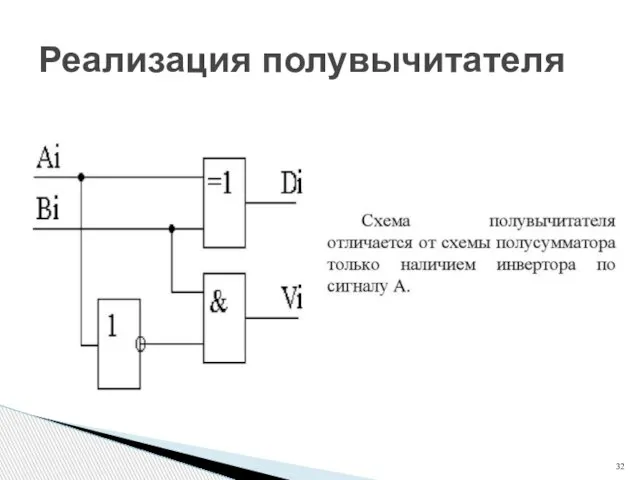
- 32. Реализация полувычитателя
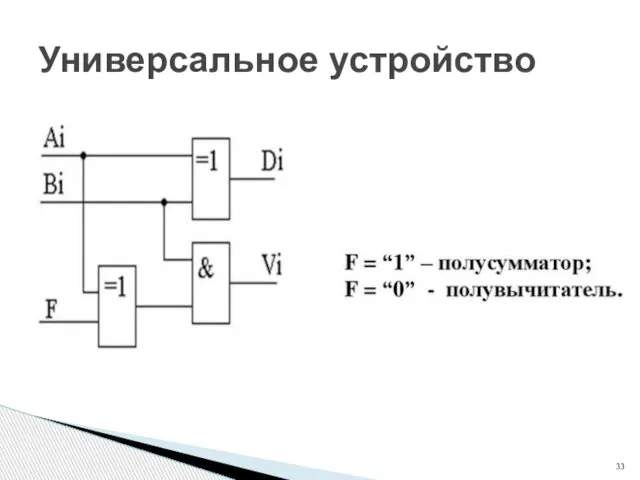
- 33. Универсальное устройство
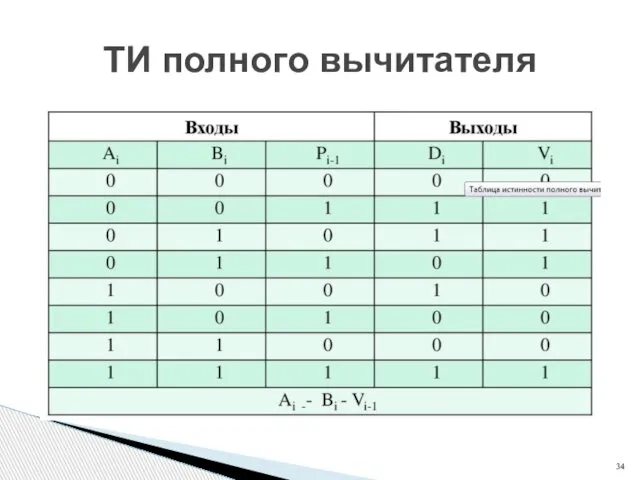
- 34. ТИ полного вычитателя
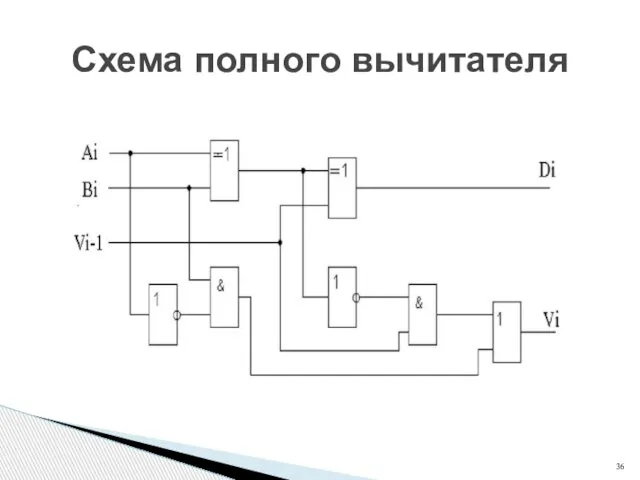
- 36. Схема полного вычитателя
- 38. Скачать презентацию






















 Программирование с использованием строковых переменных
Программирование с использованием строковых переменных Доэлектронная история вычислительной техники. (Глава 1)
Доэлектронная история вычислительной техники. (Глава 1) Программы для видеоконференций
Программы для видеоконференций Текстовые редакторы
Текстовые редакторы Методы тестирования
Методы тестирования Презентация "Декодирование" - скачать презентации по Информатике
Презентация "Декодирование" - скачать презентации по Информатике SQL. Часть II
SQL. Часть II Панели инструментов программы Autocad-2014
Панели инструментов программы Autocad-2014 Эфирная политика России
Эфирная политика России Презентация "ПРОЕКТ и основные этапы его разработки" - скачать презентации по Информатике
Презентация "ПРОЕКТ и основные этапы его разработки" - скачать презентации по Информатике Как мы познаём окружающий мир
Как мы познаём окружающий мир Неопределённость. Энтропия
Неопределённость. Энтропия Применение функции ИНДЕКС
Применение функции ИНДЕКС Медиатекст: черты и особенности
Медиатекст: черты и особенности Использование функций в табличном процессоре MS EXCEL
Использование функций в табличном процессоре MS EXCEL Матрица покрытия требований тестами
Матрица покрытия требований тестами Текстовый редактор. Тест
Текстовый редактор. Тест Кодирование и декодирование информации
Кодирование и декодирование информации Александр Шаповал
Александр Шаповал  Програмна система розпізнавання цифрового підпису
Програмна система розпізнавання цифрового підпису Блочные алгоритмы, системы шифрования
Блочные алгоритмы, системы шифрования Презентация "MSC.Dytran - 08" - скачать презентации по Информатике
Презентация "MSC.Dytran - 08" - скачать презентации по Информатике Пользовательский интерфейс
Пользовательский интерфейс Задача про числовой ряд. Лекция 4 по алгоритмизации и программированию
Задача про числовой ряд. Лекция 4 по алгоритмизации и программированию Безопасный интернет. Памятка родителям
Безопасный интернет. Памятка родителям Система условных знаков для представления информации
Система условных знаков для представления информации Топология компьютерных сетей
Топология компьютерных сетей ИСКУССТВО ХХ ВЕКА. ЖИВОПИСЬ ОТ МОДЕРНА ДО ФУТУРИЗМА
ИСКУССТВО ХХ ВЕКА. ЖИВОПИСЬ ОТ МОДЕРНА ДО ФУТУРИЗМА