Содержание
- 2. Поисковое дерево называется 2-3-деревом, если оно обладает следующими свойствами: каждая вершина x, не являющаяся листом, содержит
- 3. Каждая внутренняя вершина 2-3 –дерева является справочной и содержит две метки: а=left_max_val(v) – максимальное значение ключа
- 4. Если в 2-3-дереве только один лист, (например, 4), то это дерево имеет следующий вид: 4 3:4
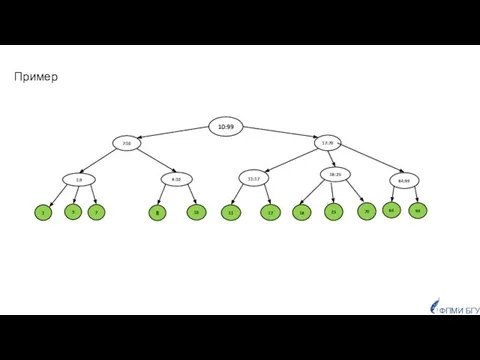
- 5. ФПМИ БГУ Пример
- 6. ТЕОРЕМА Пусть n – общее количество вершин в 2-3-дереве (включая корень и листья); l – количество
- 7. Первое неравенство доказано. ФПМИ БГУ Предположим, что теорема верна для деревьев высоты h и докажем её
- 8. ФПМИ БГУ Неравенство (2) также доказано.
- 9. Как следует из левой части неравенства (2): ТЕОРЕМА Пусть n – общее количество вершин в 2-3-дереве
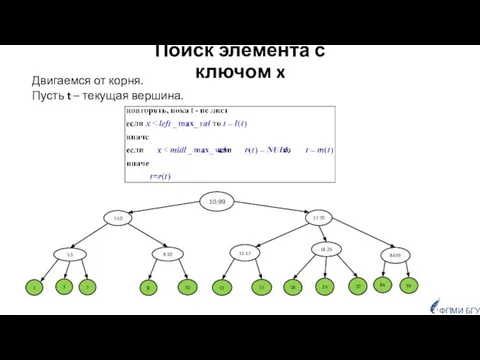
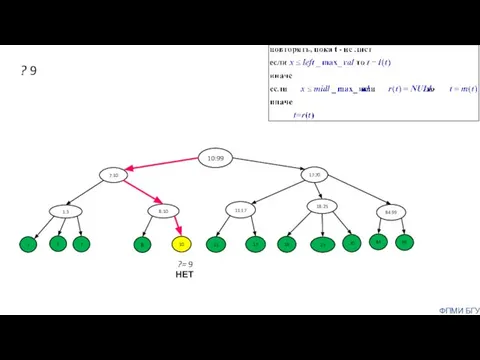
- 10. Поиск элемента с ключом x Двигаемся от корня. Пусть t – текущая вершина. ФПМИ БГУ
- 11. 10:99 18 17 11 10 8 7 3 1 11:17 8:10 1:3 84 70 25 18:25
- 12. 10:99 18 17 11 10 8 7 3 1 11:17 8:10 1:3 84 70 25 18:25
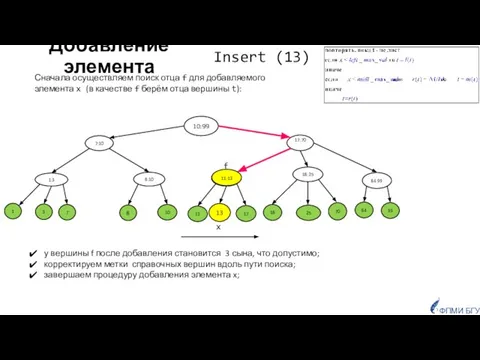
- 13. Добавление элемента 10:99 18 17 11 10 8 7 3 1 8:10 1:3 84 70 25
- 14. 10:99 18 17 11 10 8 4 1 11:17 8:9 1:4 84 70 25 18:25 4:10
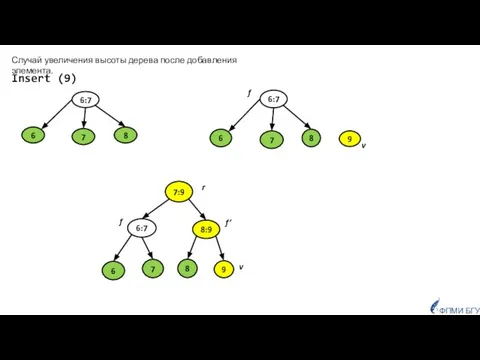
- 15. f v Случай увеличения высоты дерева после добавления элемента. ФПМИ БГУ Insert (9)
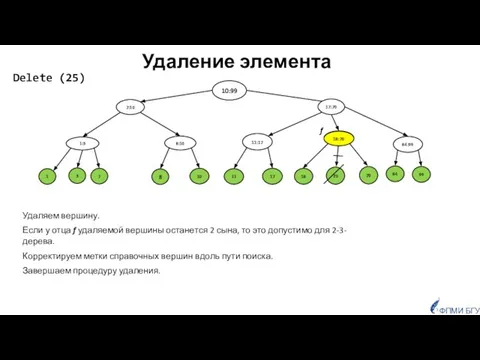
- 16. Удаление элемента 10:99 18 17 11 10 8 7 3 1 11:17 8:10 1:3 84 70
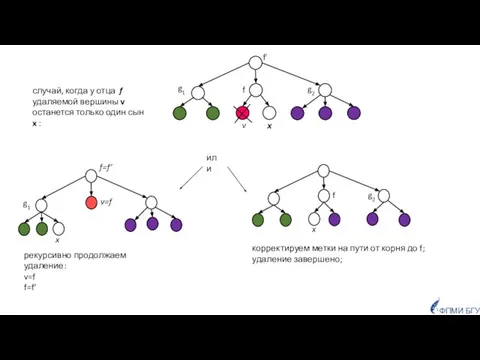
- 17. v=f рекурсивно продолжаем удаление: v=f f=f’ g1 ФПМИ БГУ случай, когда у отца f удаляемой вершины
- 18. После удаления вершины v высота дерева может уменьшится на 1: ФПМИ БГУ v f
- 19. Оценки Поиск элемента Добавление элемента Удаление элемента ФПМИ БГУ O(lоg n)
- 20. Важными дополнительными операциями, которые можно эффективно выполнять для 2-3-дерева являются: Join (T1,T2) – объединение двух 2-3-деревьев,
- 21. Join (T1,T2) – объединение двух 2-3-деревьев, при условии, что все ключи в дереве T1 меньше, чем
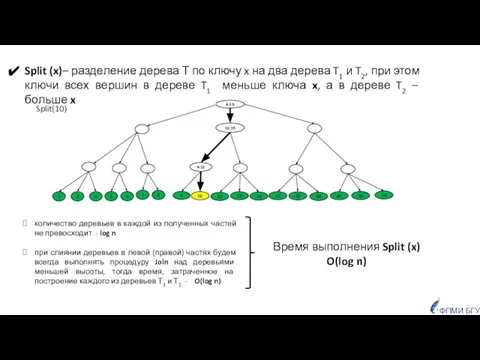
- 22. Split (x)– разделение дерева Т по ключу x на два дерева T1 и T2, при этом
- 23. 8:15 10:15 9:10 3 4 5 7 8 2 1 9 10 11 13 15 17
- 24. Удаление из дерева непрерывного участка ключей, лежащих в интервале [a,b] ФПМИ БГУ
- 25. 8:15 3:5 1:2 4:5 7:8 10:15 9:10 11:13 56:76 17:40 60:70 3 4 5 7 8
- 27. Скачать презентацию














![Удаление из дерева непрерывного участка ключей, лежащих в интервале [a,b] ФПМИ БГУ](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/567180/slide-23.jpg)

 Стандарты документирования программных средств. Лекция 4
Стандарты документирования программных средств. Лекция 4 Технологии 5G
Технологии 5G Библиография, как общественный феномен
Библиография, как общественный феномен Системы счисления. Задания
Системы счисления. Задания Презентация "КОМПЬЮТЕРНЫЕ ВИРУСЫ И АНТИВИРУСНЫЕ ПРОГРАММЫ" - скачать презентации по Информатике
Презентация "КОМПЬЮТЕРНЫЕ ВИРУСЫ И АНТИВИРУСНЫЕ ПРОГРАММЫ" - скачать презентации по Информатике Многопоточность в CLR и C#
Многопоточность в CLR и C# Информационные технологии в электротехнике и электроэнергетике
Информационные технологии в электротехнике и электроэнергетике Вспоминалки. Доступ к свойствам и методам
Вспоминалки. Доступ к свойствам и методам Информатика в играх и задачах Факультативный курс МОУ СОШ № 5 р. п. Маго Мальцева О. А.
Информатика в играх и задачах Факультативный курс МОУ СОШ № 5 р. п. Маго Мальцева О. А. Программы для работы с видео
Программы для работы с видео Локальные компьютерные сети Группа компьютеров, соединенных между собой для обмена информацией, называется компьютерной сет
Локальные компьютерные сети Группа компьютеров, соединенных между собой для обмена информацией, называется компьютерной сет Обзор языков программирования. Лекция №1
Обзор языков программирования. Лекция №1 Оперативная память
Оперативная память Paint графикалық редакторы
Paint графикалық редакторы Антивирусы что это и как работают В этом проекте я решил рассказать о программах которые называют антивирусы. Что это за программ
Антивирусы что это и как работают В этом проекте я решил рассказать о программах которые называют антивирусы. Что это за программ Главные правила классической типографики
Главные правила классической типографики Линейный алгоритм
Линейный алгоритм Презентация "Арифметическая и геометрическая прогрессия" - скачать презентации по Информатике
Презентация "Арифметическая и геометрическая прогрессия" - скачать презентации по Информатике Прикладне програмування
Прикладне програмування How to Get Published in a Research Journal
How to Get Published in a Research Journal Цели и направления внедрения средств ИКТ в образование
Цели и направления внедрения средств ИКТ в образование Внутренние и периферийные устройства компьютера
Внутренние и периферийные устройства компьютера Исключительные ситуации
Исключительные ситуации Основы объектно-ориентированного визуального программирования Visual Basic (VB)
Основы объектно-ориентированного визуального программирования Visual Basic (VB) Мониторинг медиа ресурсов в сети Интернет
Мониторинг медиа ресурсов в сети Интернет Урок по теме: «Введение в графику в языке программирования Turbo Pascal» Автор: Казначей, учитель информатики
Урок по теме: «Введение в графику в языке программирования Turbo Pascal» Автор: Казначей, учитель информатики How to apply NLA-5&15S Preset
How to apply NLA-5&15S Preset Создание базы данных
Создание базы данных