- Главная
- Информатика
- Остов графа (покрывающее дерево)

Содержание
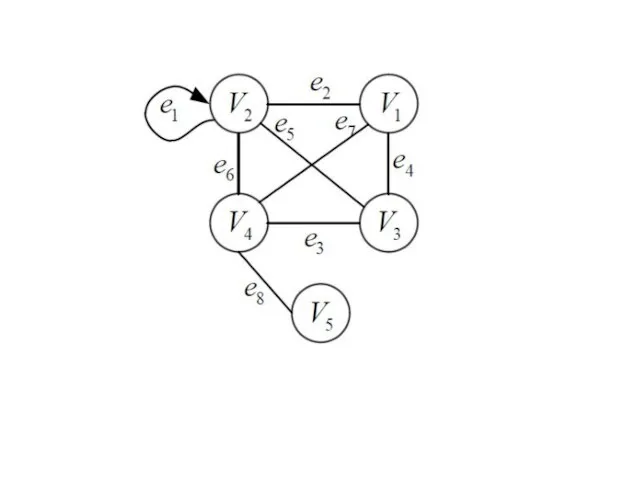
- 2. Пусть G(V, Е) — граф. Остовный подграф графа G(V, E) — это подграф, содержащий все вершины.
- 3. Алгоритм Краскала Раскраска графа: синим цветом окрашиваются ребра, включаемые в покрывающее дерево; оранжевым цветом окрашиваются ребра,
- 5. Начало: Все рёбра графа G (V,E) не окрашены и ни один из букетов не формирован. Шаг
- 6. Шаг 3. После выбора ребра возможны 4 случая: А. Обе концевые вершины выбранного ребра принадлежат одному
- 7. Алгоритм Краскала Вход: список Е рёбер графа G с длинами, упорядоченный в порядке возрастания длин. Выход:
- 8. Алгоритм Прима Начало: Дан граф G (V,E) — связный и взвешенный. Все ребра упорядочены по возрастанию
- 9. После выбора ребра возможны 2 случая: А. Ребро составляет цикл с существующими ребрами дерева. Тогда удаляем
- 10. a[v] — это ближайшая к v вершина, уже включённая в остов, b[v] — это длина ребра,
- 11. Алгоритм: select u∈V { выбираем произвольную вершину } S={u} { S - множество вершин, включённых в
- 12. for i =1 to p - 1 do х: = ∞ {начальное значение для поиска ближайшей
- 14. Скачать презентацию
Слайд 2
Пусть G(V, Е) — граф. Остовный подграф графа G(V, E) —
Пусть G(V, Е) — граф. Остовный подграф графа G(V, E) —
это подграф, содержащий все вершины. Остовный подграф, являющийся деревом, называется остовом или каркасом (лес).
Букет – множество вершин, принадлежащих одной компоненте связности.
Букет – множество вершин, принадлежащих одной компоненте связности.
Слайд 3
Алгоритм Краскала
Раскраска графа:
синим цветом окрашиваются ребра, включаемые в покрывающее дерево;
оранжевым
Алгоритм Краскала
Раскраска графа:
синим цветом окрашиваются ребра, включаемые в покрывающее дерево;
оранжевым
цветом окрашиваются ребра, не включаемые в покрывающее дерево, т.к. они образуют цикл с синими ребрами или являются петлями.
Существует 2 случая связности графа:
1 Если G (V,E) – связный граф, то построение покрывающего дерева по алгоритму Краскала заканчивается, когда количество ребер, окрашенных в синий цвет, становится равным (p-1) .
2 Если G (V,E) – несвязный граф, то построение покрывающего дерева по алгоритму Краскала заканчивается после раскраски всех ребер графа. Число покрывающих деревьев в таком лесу будет равно числу букетов.
Существует 2 случая связности графа:
1 Если G (V,E) – связный граф, то построение покрывающего дерева по алгоритму Краскала заканчивается, когда количество ребер, окрашенных в синий цвет, становится равным (p-1) .
2 Если G (V,E) – несвязный граф, то построение покрывающего дерева по алгоритму Краскала заканчивается после раскраски всех ребер графа. Число покрывающих деревьев в таком лесу будет равно числу букетов.
Слайд 4
Слайд 5
Начало: Все рёбра графа G (V,E) не окрашены и ни один
из
Начало: Все рёбра графа G (V,E) не окрашены и ни один
из
букетов не формирован.
Шаг 1. Все петли окрасить в оранжевый цвет.
Шаг 2. Из упорядоченного множества E выбирается первое
ребро, не являющееся петлей. Это ребро окрашивается в синий цвет и формируется букет, в который включаются концевые вершины выбранного ребра.
Шаг 3. Из оставшихся ребер выбирается первое неокрашенное ребро, которое не является петлей. Если в графе такого ребра нет, следует закончить процедуру и перейти к шагу 4.
Шаг 4. Если все ребра окрашены, следует закончить процедуру. Синие ребра образуют покрывающее дерево (лес). В противном случае вернуться к началу шага 2.
Шаг 1. Все петли окрасить в оранжевый цвет.
Шаг 2. Из упорядоченного множества E выбирается первое
ребро, не являющееся петлей. Это ребро окрашивается в синий цвет и формируется букет, в который включаются концевые вершины выбранного ребра.
Шаг 3. Из оставшихся ребер выбирается первое неокрашенное ребро, которое не является петлей. Если в графе такого ребра нет, следует закончить процедуру и перейти к шагу 4.
Шаг 4. Если все ребра окрашены, следует закончить процедуру. Синие ребра образуют покрывающее дерево (лес). В противном случае вернуться к началу шага 2.
Слайд 6
Шаг 3. После выбора ребра возможны 4 случая:
А. Обе концевые вершины
Шаг 3. После выбора ребра возможны 4 случая:
А. Обе концевые вершины
выбранного ребра принадлежат одному и тому же букету. В этом случае ребро окрашивается в оранжевый цвет.
Б. Одна из концевых вершин ребра принадлежит существующему букету, а другая – не принадлежит ни одному из уже сформированных букетов. В этом случае ребро окрашивается в синий цвет, и его вторая концевая вершина включается в букет, которому принадлежит первая концевая вершина.
В. Концевые вершины выбранного ребра принадлежат
различным букетам. В этом случае ребро окрашивается в синий цвет, а оба букета, которым принадлежат его концевые вершины, объединяем в новый букет с меньшей нумерацией.
Г. Ни одна из концевых вершин не принадлежит ни одному из формированных букетов. В этом случае ребро окрашивается в синий цвет и формируется новый букет из концевых вершин этого ребра.
Б. Одна из концевых вершин ребра принадлежит существующему букету, а другая – не принадлежит ни одному из уже сформированных букетов. В этом случае ребро окрашивается в синий цвет, и его вторая концевая вершина включается в букет, которому принадлежит первая концевая вершина.
В. Концевые вершины выбранного ребра принадлежат
различным букетам. В этом случае ребро окрашивается в синий цвет, а оба букета, которым принадлежат его концевые вершины, объединяем в новый букет с меньшей нумерацией.
Г. Ни одна из концевых вершин не принадлежит ни одному из формированных букетов. В этом случае ребро окрашивается в синий цвет и формируется новый букет из концевых вершин этого ребра.
Слайд 7
Алгоритм Краскала
Вход: список Е рёбер графа G с длинами, упорядоченный в
Алгоритм Краскала
Вход: список Е рёбер графа G с длинами, упорядоченный в
порядке возрастания длин.
Выход: множество T рёбер кратчайшего остова.
T = {}
k = 1 { номер рассматриваемого ребра }
for i from 1 to p-1 do
while (T + E[k]) - цикл do
k = k + 1 { пропустить это ребро }
T= T + Е[k] { добавить это ребро в остов }
k = k + 1
end
Выход: множество T рёбер кратчайшего остова.
T = {}
k = 1 { номер рассматриваемого ребра }
for i from 1 to p-1 do
while (T + E[k]) - цикл do
k = k + 1 { пропустить это ребро }
T= T + Е[k] { добавить это ребро в остов }
k = k + 1
end
Слайд 8
Алгоритм Прима
Начало: Дан граф G (V,E) — связный и взвешенный.
Все ребра
Алгоритм Прима
Начало: Дан граф G (V,E) — связный и взвешенный.
Все ребра
упорядочены по возрастанию весов и по
нумерации для ребер с одинаковыми весами. Петли удалены. Из кратных ребер оставляем ребро с минимальным весом.
Минимальное покрывающее дерево T не построено.
Букет не сформирован.
Шаг 1. Выбираем из упорядоченного множества E первое
ребро (i,j) и включаем его в дерево T .
Обе концевые вершины включаем в букет { i, j} .
Удаляем из E выбранное ребро.
Шаг 2. Из множества E выбираем первое ребро, инцидентное какой-либо вершине из сформированного букета.
нумерации для ребер с одинаковыми весами. Петли удалены. Из кратных ребер оставляем ребро с минимальным весом.
Минимальное покрывающее дерево T не построено.
Букет не сформирован.
Шаг 1. Выбираем из упорядоченного множества E первое
ребро (i,j) и включаем его в дерево T .
Обе концевые вершины включаем в букет { i, j} .
Удаляем из E выбранное ребро.
Шаг 2. Из множества E выбираем первое ребро, инцидентное какой-либо вершине из сформированного букета.
Слайд 9
После выбора ребра возможны 2 случая:
А. Ребро составляет цикл с существующими
После выбора ребра возможны 2 случая:
А. Ребро составляет цикл с существующими
ребрами
дерева. Тогда удаляем его из E и возвращаемся к
началу шага 2.
Б. Ребро не образует с существующими ребрами дерева
цикл. Тогда новая вершина добавляется к вершинам
сформированного букета. Ребро добавляется в дерево. Далее возвращаемся к началу шага 2.
Шаг 3. Если дерево (букет) включает в себя все вершины графа,
то минимальное покрывающее дерево построено.
(Если дерево не включает в себя все вершины, то граф не является связным.)
дерева. Тогда удаляем его из E и возвращаемся к
началу шага 2.
Б. Ребро не образует с существующими ребрами дерева
цикл. Тогда новая вершина добавляется к вершинам
сформированного букета. Ребро добавляется в дерево. Далее возвращаемся к началу шага 2.
Шаг 3. Если дерево (букет) включает в себя все вершины графа,
то минимальное покрывающее дерево построено.
(Если дерево не включает в себя все вершины, то граф не является связным.)
Слайд 10
a[v] — это ближайшая к v вершина, уже включённая в остов,
a[v] — это ближайшая к v вершина, уже включённая в остов,
b[v] — это длина ребра, соединяющего v с остовом. Если вершину v ещё нельзя соединить с остовом одним ребром, то a[v]: = 0, b[v]: = ∞.
Вход: граф G(V, E), заданный матрицей длин рёбер С.
Выход: множество Т рёбер кратчайшего остова.
Слайд 11
Алгоритм:
select u∈V { выбираем произвольную вершину }
S={u} { S -
Алгоритм:
select u∈V { выбираем произвольную вершину }
S={u} { S -
множество вершин, включённых в кратчайший остов }
T = ∅ { T - множество рёбер, включённых в кратчайший остов }
for v ∈ V - u do
if v ∈Г(u) then
a[v]: = u { u — ближайшая вершина остова }
b[v]: = С[u, v] { C[u, v] — длина соответствующего ребра }
else
a[v]: = 0 { ближайшая вершина остова неизвестна }
b[v]: = ∞ { и расстояние также неизвестно }
end if
end for
T = ∅ { T - множество рёбер, включённых в кратчайший остов }
for v ∈ V - u do
if v ∈Г(u) then
a[v]: = u { u — ближайшая вершина остова }
b[v]: = С[u, v] { C[u, v] — длина соответствующего ребра }
else
a[v]: = 0 { ближайшая вершина остова неизвестна }
b[v]: = ∞ { и расстояние также неизвестно }
end if
end for
Слайд 12
for i =1 to p - 1 do
х:
for i =1 to p - 1 do
х:
= ∞ {начальное значение для поиска ближайшей вершины}
for v ∈ V \ S do
if b[v] < х then
w = v { нашли более близкую вершину }
x = b[v] { и расстояние до неё }
end if
end for
S = S + w { добавляем найденную вершину в остов }
T =T + (a[w],w) { добавляем найденное ребро в остов }
for v ∈ Г(w) do
if v ∉ S then
if b[v] >C[v,w] then
a[v]: = w { изменяем ближайшую вершину остова }
b[v]: = C[v, w] { и длину ведущего к ней ребра }
end if
end if
end for end for
for v ∈ V \ S do
if b[v] < х then
w = v { нашли более близкую вершину }
x = b[v] { и расстояние до неё }
end if
end for
S = S + w { добавляем найденную вершину в остов }
T =T + (a[w],w) { добавляем найденное ребро в остов }
for v ∈ Г(w) do
if v ∉ S then
if b[v] >C[v,w] then
a[v]: = w { изменяем ближайшую вершину остова }
b[v]: = C[v, w] { и длину ведущего к ней ребра }
end if
end if
end for end for
- Предыдущая
Java. Типы данных, операторы, литералыСледующая -
Основы православной культуры






![a[v] — это ближайшая к v вершина, уже включённая в остов,](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/499020/slide-9.jpg)


 Операционная система
Операционная система Алгоритмы и анализ сложности. Структуры данных. Деревья. (Тема 2)
Алгоритмы и анализ сложности. Структуры данных. Деревья. (Тема 2) Устройства ввода текстовой и графической информации (сканер)
Устройства ввода текстовой и графической информации (сканер) Разработка модуля информационной системы по учету фактического расхода покупных комплектующих изделий для организации
Разработка модуля информационной системы по учету фактического расхода покупных комплектующих изделий для организации Фреймворк Laravel
Фреймворк Laravel Одобрение Онлайн по объектам на Витрине ДомКлик
Одобрение Онлайн по объектам на Витрине ДомКлик Презентация "Алгоритм – как модель деятельности" - скачать презентации по Информатике
Презентация "Алгоритм – как модель деятельности" - скачать презентации по Информатике О мероприятиях по реализации информационной безопасности ГАС Правосудие
О мероприятиях по реализации информационной безопасности ГАС Правосудие Android платформасы
Android платформасы ТМО как научная дисциплина
ТМО как научная дисциплина Деструктивное поведение
Деструктивное поведение Аттестационная работа. Современные компьютерные техноголии
Аттестационная работа. Современные компьютерные техноголии Технологии проектирования информационных систем. Применение сетей Петри для моделирования бизнес-процессов
Технологии проектирования информационных систем. Применение сетей Петри для моделирования бизнес-процессов Правила оформления текстовых документов по ГОСТу 2.105 – 95
Правила оформления текстовых документов по ГОСТу 2.105 – 95 Редактирование текста – этап подготовки документа на компьютере, в ходе которого исправляются обнаруженные ошибки (например в п
Редактирование текста – этап подготовки документа на компьютере, в ходе которого исправляются обнаруженные ошибки (например в п Десктоп версия
Десктоп версия Базы данных. Теоретические основы
Базы данных. Теоретические основы Воркбук Прототип landing page
Воркбук Прототип landing page Карточная коллекционная игра
Карточная коллекционная игра Технология мультимедиа
Технология мультимедиа Информационная безопасность
Информационная безопасность День безопасного Интернета
День безопасного Интернета Партнерский портал РАМК
Партнерский портал РАМК Если вы хотите устроиться на работу
Если вы хотите устроиться на работу Учебно-методический комплекс Front Page 2003
Учебно-методический комплекс Front Page 2003 Форматы звуковых файлов
Форматы звуковых файлов Инструкция ОИ по работе с обращениями
Инструкция ОИ по работе с обращениями Презентация "основы визуальной грамотности " - скачать презентации по Информатике
Презентация "основы визуальной грамотности " - скачать презентации по Информатике