- Главная
- Информатика
- Поиск пути наименьшей длины

Содержание
- 2. Поиск расстояния между всеми парами вершин. Алгоритм Уоршалла-Флойда Вход: матрица С длин дуг. Выход: матрица Т
- 3. for i from 1 to p do for j from 1 to p do for k
- 5. Пусть G = – взвешенный орграф без петель. Поиск пути наименьшей длины между вершинами s (начало)
- 6. H[s]: = 0; T[s]: = 0; X [s] = 1 v = s { текущая вершина
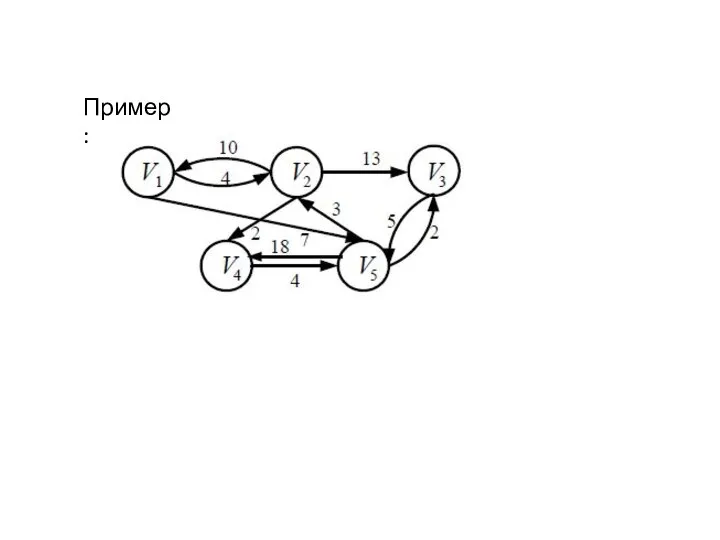
- 7. Пример:
- 13. Скачать презентацию
Слайд 2
Поиск расстояния между всеми парами вершин. Алгоритм Уоршалла-Флойда
Вход: матрица С
Поиск расстояния между всеми парами вершин. Алгоритм Уоршалла-Флойда
Вход: матрица С
длин дуг.
Выход: матрица Т длин путей и матрица H самих путей.
for г from 1 to p do
for j from 1 to p do
T[i,j] = C[i,j] { инициализация }
if C[i,j] = ∞ then H[i, j] = 0 { нет дуги из i в j }
else H[i,j]: =j
end
end
Выход: матрица Т длин путей и матрица H самих путей.
for г from 1 to p do
for j from 1 to p do
T[i,j] = C[i,j] { инициализация }
if C[i,j] = ∞ then H[i, j] = 0 { нет дуги из i в j }
else H[i,j]: =j
end
end
Слайд 3
for i from 1 to p do
for j from
for i from 1 to p do
for j from
1 to p do
for k from 1 to p do
if i≠ j & T[j, i] ≠ ∞ & i ≠k & T[i,k] ≠ ∞ &
(T[j, k] = ∞ V T[j, k] > T[j,i] + T[i,k])
then H[j,k] = H[j, i] { запомнить новый путь }
T[j,k]: = T[j, i] + T[i, k] { и его длину }
end
end
for j from 1 to p do
if T[j,j]<0 then stop { нет решения}
end
end
for k from 1 to p do
if i≠ j & T[j, i] ≠ ∞ & i ≠k & T[i,k] ≠ ∞ &
(T[j, k] = ∞ V T[j, k] > T[j,i] + T[i,k])
then H[j,k] = H[j, i] { запомнить новый путь }
T[j,k]: = T[j, i] + T[i, k] { и его длину }
end
end
for j from 1 to p do
if T[j,j]<0 then stop { нет решения}
end
end
Слайд 4
Слайд 5
Пусть G = – взвешенный орграф без петель.
Поиск пути наименьшей длины
Пусть G =
Поиск пути наименьшей длины
между вершинами s (начало) и t(конец).
Алгоритм Дейкстры
Вход: орграф G(V,E), заданный матрицей длин дуг С pхp
s и t — вершины графа.
Выход: векторы T и H длиной p.
Если вершина v лежит на кратчайшем пути от s к t,
то T[v] — длина кратчайшего пути от s к v;
H[v] — вершина, непосредственно предшествующая v на кратчайшем пути.
for v from 1 to p do
T[v] = ∞ { кратчайший путь неизвестен }
X [v] = 0 { все вершины не отмечены }
end
Алгоритм Дейкстры
Вход: орграф G(V,E), заданный матрицей длин дуг С pхp
s и t — вершины графа.
Выход: векторы T и H длиной p.
Если вершина v лежит на кратчайшем пути от s к t,
то T[v] — длина кратчайшего пути от s к v;
H[v] — вершина, непосредственно предшествующая v на кратчайшем пути.
for v from 1 to p do
T[v] = ∞ { кратчайший путь неизвестен }
X [v] = 0 { все вершины не отмечены }
end
Слайд 6
H[s]: = 0; T[s]: = 0; X [s] = 1
v
H[s]: = 0; T[s]: = 0; X [s] = 1
v
= s { текущая вершина }
М: { обновление пометок }
for u in Г(v) do
if X[u] = 0 & T[u] > T[v] + C[v, u]
then T[u]=T[v]+C[v,u] { найден более короткий путь }
H[u] = v { запоминаем его }
end
m = ∞; v=0 { поиск конца кратчайшего пути }
for u from 1 to p do
if X[u] = 0 & T[u] < m
then v= u; m: = T[u]
end
if v = 0 then
stop { нет пути из s в t }
if v = t then stop { найден кратчайший путь из s в t }
X[v] = 1 { найден кратчайший путь из s в v }
goto M
М: { обновление пометок }
for u in Г(v) do
if X[u] = 0 & T[u] > T[v] + C[v, u]
then T[u]=T[v]+C[v,u] { найден более короткий путь }
H[u] = v { запоминаем его }
end
m = ∞; v=0 { поиск конца кратчайшего пути }
for u from 1 to p do
if X[u] = 0 & T[u] < m
then v= u; m: = T[u]
end
if v = 0 then
stop { нет пути из s в t }
if v = t then stop { найден кратчайший путь из s в t }
X[v] = 1 { найден кратчайший путь из s в v }
goto M
Слайд 7
Пример:
Пример:
Слайд 8
Слайд 9
Слайд 10
Слайд 11




![H[s]: = 0; T[s]: = 0; X [s] = 1 v](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/652712/slide-5.jpg)




 Компьютерные игры «за» и «против»
Компьютерные игры «за» и «против»  Информационные системы. Данные. Информация. Знания. Базы данных. База знаний. Программное обеспечение
Информационные системы. Данные. Информация. Знания. Базы данных. База знаний. Программное обеспечение Системы счисления
Системы счисления СУБД ACCESS. Создание таблиц, запросов. Лекция 7-2
СУБД ACCESS. Создание таблиц, запросов. Лекция 7-2 Электронная почта ( e-mail )
Электронная почта ( e-mail ) Возможности централизованного мониторинга региональной ИТ-инфраструктуры средствами подсистемы Управление ИТ-инфраструктурой
Возможности централизованного мониторинга региональной ИТ-инфраструктуры средствами подсистемы Управление ИТ-инфраструктурой Управляющие операторы
Управляющие операторы Разработка автоматической системы контроля уровня СО2 в помещении
Разработка автоматической системы контроля уровня СО2 в помещении Реляционная алгебра
Реляционная алгебра Знаки и знаковые системы
Знаки и знаковые системы Компьютнрные сети. Информационные вычислительные сети
Компьютнрные сети. Информационные вычислительные сети Информация и ее свойства 10 класс гимназия №22 г. Майкоп
Информация и ее свойства 10 класс гимназия №22 г. Майкоп Standart funksiýalar: modul; sanyň kwadraty
Standart funksiýalar: modul; sanyň kwadraty TDA и TDAмеждународный. Первое издание в цифрах
TDA и TDAмеждународный. Первое издание в цифрах Безопасность школьников в сети интернет
Безопасность школьников в сети интернет Отчет по SMM-продвижению Аквакласс за период с 19.06.17 по 19.07.17
Отчет по SMM-продвижению Аквакласс за период с 19.06.17 по 19.07.17 Элементы статистической обработки данных 7 класс
Элементы статистической обработки данных 7 класс  Организационные аспекты процесса тестирования. (Лекция 8)
Организационные аспекты процесса тестирования. (Лекция 8) Назначение и виды операционных систем. Операции с файлами и папками
Назначение и виды операционных систем. Операции с файлами и папками Codecraft PHP. PHP цикл do...while
Codecraft PHP. PHP цикл do...while Работа в MS Office 365. Лабораторная работа 3
Работа в MS Office 365. Лабораторная работа 3 Правовые и этические аспекты использования интернета
Правовые и этические аспекты использования интернета Выпускная работа на тему: Выполнила воспитатель Инжавинской специальной (коррекционной) шк
Выпускная работа на тему: Выполнила воспитатель Инжавинской специальной (коррекционной) шк Построение таблиц истинности и логических функций
Построение таблиц истинности и логических функций Векторные графические редакторы
Векторные графические редакторы Решение уравнений и систем уравнений в MathCAD
Решение уравнений и систем уравнений в MathCAD Python. Занятие 1
Python. Занятие 1 База данных (БД)
База данных (БД)