Содержание
- 2. 16.02.2016 Динамическое программирование АНАЛОГИИ Решение методом динамического программирования Задачи: Перемножение цепочки матриц Оптимальные БДП Задача Х
- 3. 16.02.2016 Динамическое программирование Оценка количества узлов дерева Оценить количество узлов дерева в общем случае можно подсчётом
- 4. 16.02.2016 Динамическое программирование Начальное условие p1 = 1. Далее p2 = p1 p1 = 1, p3
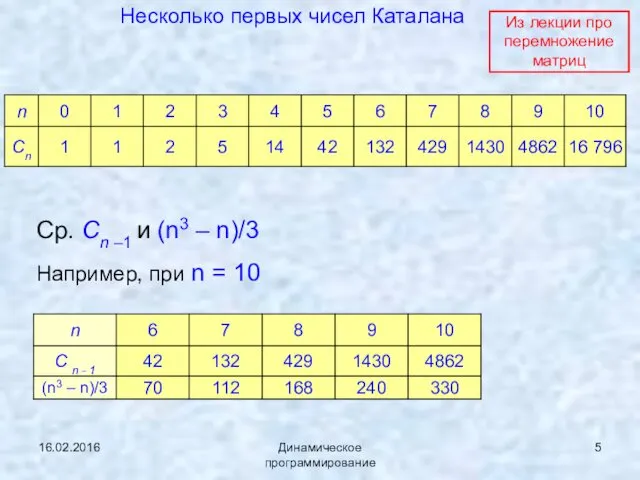
- 5. 16.02.2016 Динамическое программирование Несколько первых чисел Каталана Ср. Сn –1 и (n3 – n)/3 Например, при
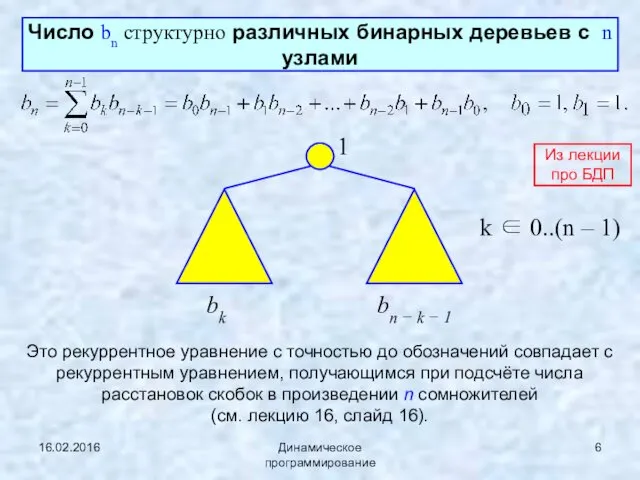
- 6. 16.02.2016 Динамическое программирование Число bn структурно различных бинарных деревьев с n узлами bk bn − k
- 7. 16.02.2016 Динамическое программирование b2 = b0 b1 + b1 b0 = 2, b3 = b0 b2
- 8. Решение методом динамического программирования Структура оптимального решения Рекуррентное соотношение Вычисление оптимальной стоимости (по рекуррентному соотношению) Построение
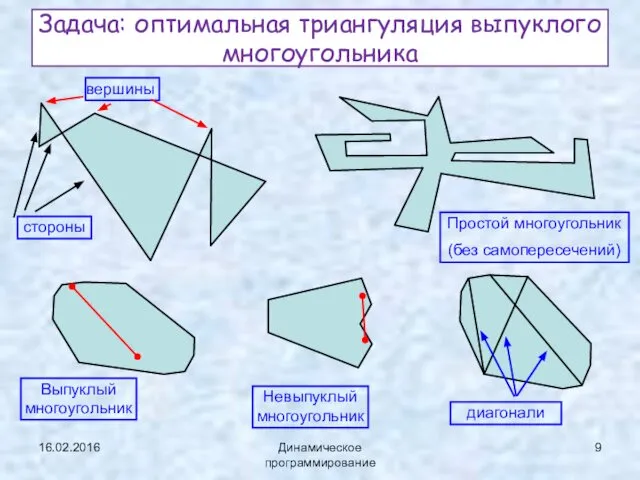
- 9. 16.02.2016 Динамическое программирование Задача: оптимальная триангуляция выпуклого многоугольника
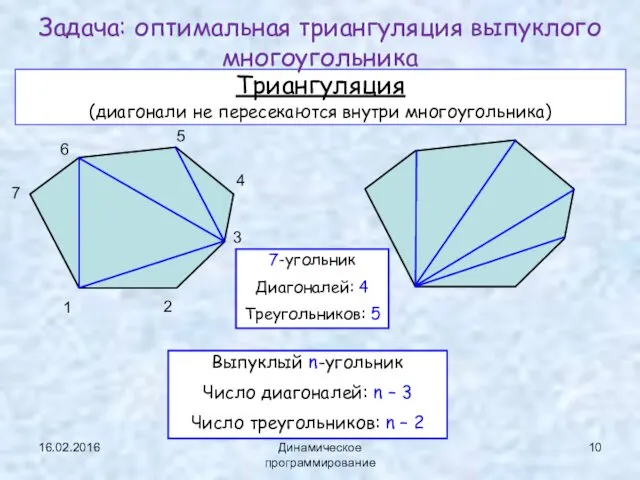
- 10. 16.02.2016 Динамическое программирование Триангуляция (диагонали не пересекаются внутри многоугольника) Задача: оптимальная триангуляция выпуклого многоугольника Выпуклый n-угольник
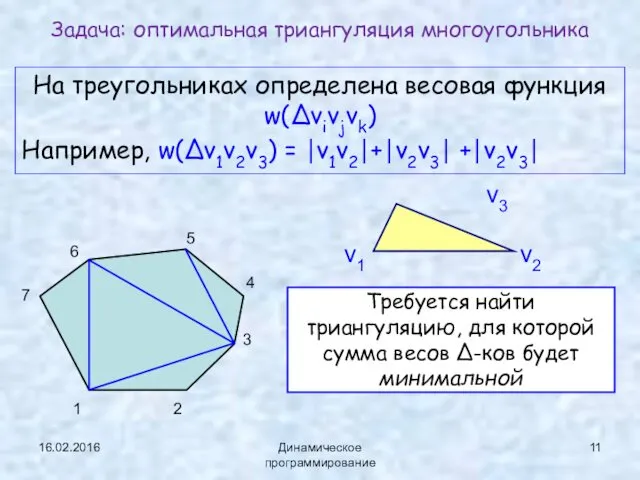
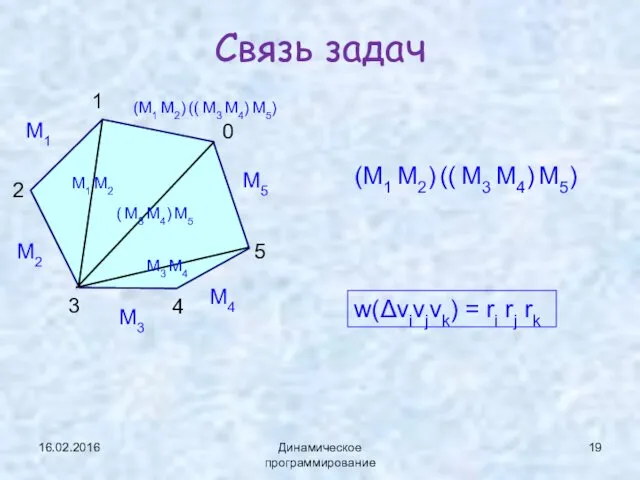
- 11. 16.02.2016 Динамическое программирование На треугольниках определена весовая функция w(Δvivjvk) Например, w(Δv1v2v3) = ⎪v1v2⎪+⎪v2v3⎪ +⎪v2v3⎪ Задача: оптимальная
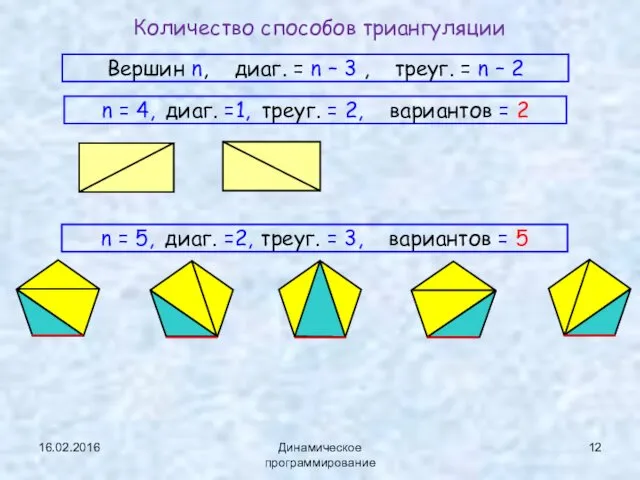
- 12. 16.02.2016 Динамическое программирование Количество способов триангуляции Вершин n, диаг. = n – 3 , треуг. =
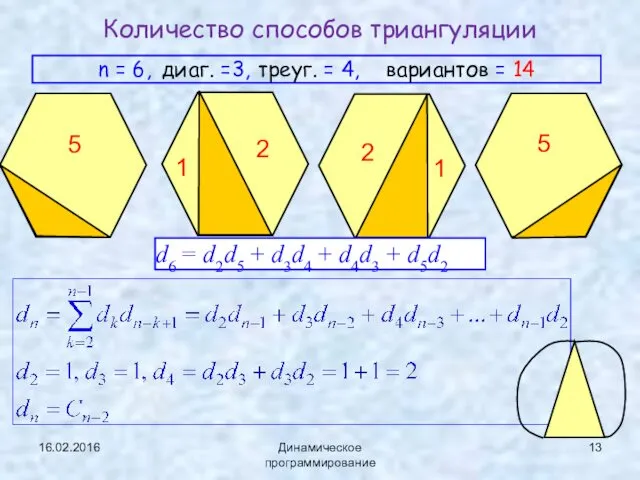
- 13. 16.02.2016 Динамическое программирование Количество способов триангуляции n = 6, диаг. =3, треуг. = 4, вариантов =
- 14. 16.02.2016 Динамическое программирование Рекуррентная формула для веса оптимальной триангуляции многоугольника (ОТМ), 1 mij – вес ОТМ
- 15. Динамическое программирование Вычисление таблиц: mi,i+1 = 0, {при i=1..n-1} mi,i+2 = w(Δi,i+1,i+2), {при i=1..n-2} mi,i+3 =…
- 16. 16.02.2016 Динамическое программирование Рекуррентная формула для веса оптимальной триангуляции многоугольника (ОТМ), 2 mij – вес ОТМ
- 17. 16.02.2016 Динамическое программирование Упражнения Доказать, что триангуляция n–угольника содержит n-2 треугольника и n-3 диагоналей. Пусть вес
- 18. 16.02.2016 Динамическое программирование Связь задач 1 2 3 4 5 0 M1 M2 M3 M4 M5
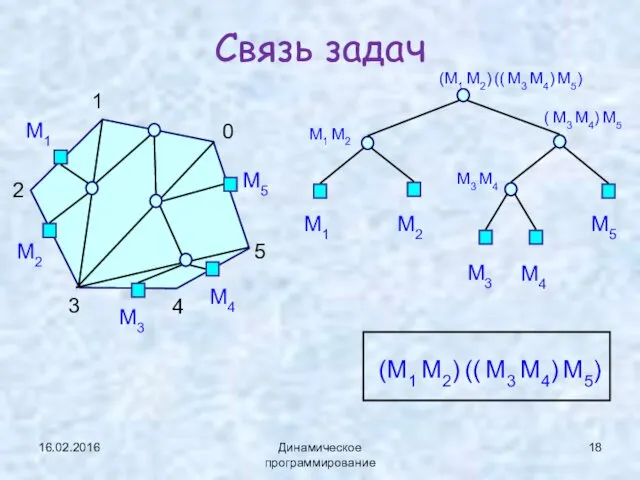
- 19. 16.02.2016 Динамическое программирование Связь задач 1 2 3 4 5 0 (M1 M2) (( M3 M4)
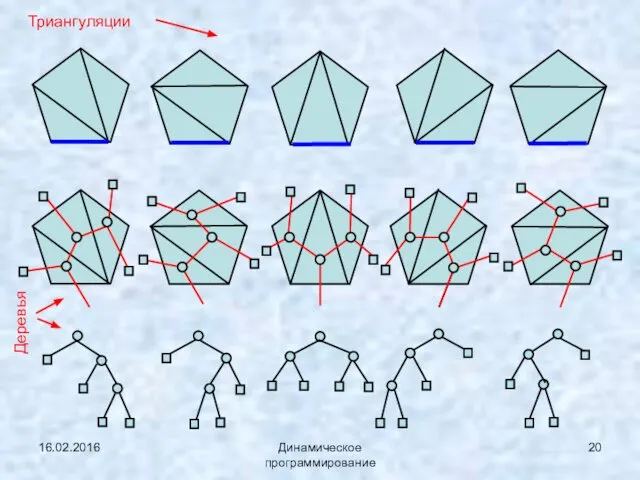
- 20. 16.02.2016 Динамическое программирование Триангуляции Деревья
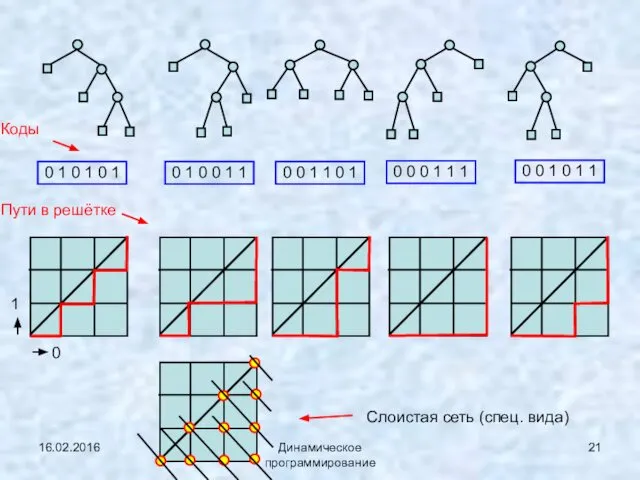
- 21. 16.02.2016 Динамическое программирование 0 1 0 1 0 1 0 1 0 0 1 1 0
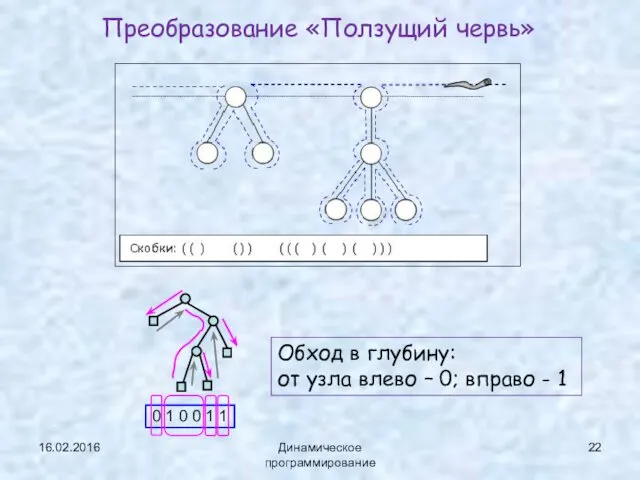
- 22. Преобразование «Ползущий червь» 16.02.2016 Динамическое программирование 0 1 0 0 1 1 Обход в глубину: от
- 23. Литература Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ : учеб./ М.: МЦМНО, 1999.
- 25. Скачать презентацию










 Сервис Офисы и приемные. Предварительная запись на прием
Сервис Офисы и приемные. Предварительная запись на прием Класс больших компьютеров
Класс больших компьютеров Основы LINQ
Основы LINQ Презентация "Анимированные ребусы" - скачать презентации по Информатике
Презентация "Анимированные ребусы" - скачать презентации по Информатике Управление памятью в ОС Windows
Управление памятью в ОС Windows Программное обеспечение
Программное обеспечение Процеси. Process Control Block і контекст процесу
Процеси. Process Control Block і контекст процесу Использование сервисов телекоммуникационных сетей для доступа к образовательным мультимедиа-ресурсам
Использование сервисов телекоммуникационных сетей для доступа к образовательным мультимедиа-ресурсам Программирование линейных алгоритмов
Программирование линейных алгоритмов Машинно-зависимые и машинно-независимые свойства ОС
Машинно-зависимые и машинно-независимые свойства ОС Библиотека. ПК
Библиотека. ПК Достижение целевого показателя
Достижение целевого показателя Компьютер , как универсальное средство обработки информации.
Компьютер , как универсальное средство обработки информации. Примеры символьной обработки (язык C, лекция 9)
Примеры символьной обработки (язык C, лекция 9) Гайд на Aristois
Гайд на Aristois Мультимедийные технологии Борисов В.А. Красноармейский филиал ГОУ ВПО «Академия народного хозяйства при Правительстве РФ»
Мультимедийные технологии Борисов В.А. Красноармейский филиал ГОУ ВПО «Академия народного хозяйства при Правительстве РФ»  Государственное бюджетное общеобразовательное учреждение лицей 95 Калининского района г. Санкт - Петербурга Паскаль. Циклы. Р
Государственное бюджетное общеобразовательное учреждение лицей 95 Калининского района г. Санкт - Петербурга Паскаль. Циклы. Р Многообразие периферийных устройств
Многообразие периферийных устройств МоиДепутаты.РФ - Портал для диалога с представителями власти
МоиДепутаты.РФ - Портал для диалога с представителями власти Протоколы взаимодействия между административными доменами провайдеров
Протоколы взаимодействия между административными доменами провайдеров FrontЕnd development. Вводное занятие
FrontЕnd development. Вводное занятие Лекция 16. Сущность внешнего силового электромагнитного воздействия (СЭМВ) как угроза безопасности информации в АС
Лекция 16. Сущность внешнего силового электромагнитного воздействия (СЭМВ) как угроза безопасности информации в АС Магистрально-модульный принцип построения компьютера
Магистрально-модульный принцип построения компьютера Программирование алгоритмов на языке Python. Работа с файлами
Программирование алгоритмов на языке Python. Работа с файлами Протоколы.Интерфейсы. Заголовки. Назначение уровней
Протоколы.Интерфейсы. Заголовки. Назначение уровней Базы данных. Основное определение. Классификация БД
Базы данных. Основное определение. Классификация БД Функция распределения
Функция распределения АИС Продажа автобусных билетов
АИС Продажа автобусных билетов