Построение и анализ алгоритмов. Динамическое программирование. Оптимальные деревья поиска. (Лекция 4)
Содержание
- 2. 16.02.2016 Динамическое программирование Пример 3. Оптимальные деревья поиска См. начало в Лекции 3. См. также раздел
- 3. Оптимальные деревья поиска Ранее при рассмотрении БДП, как правило, предполагалось, что для поиска различные ключи предъявляются
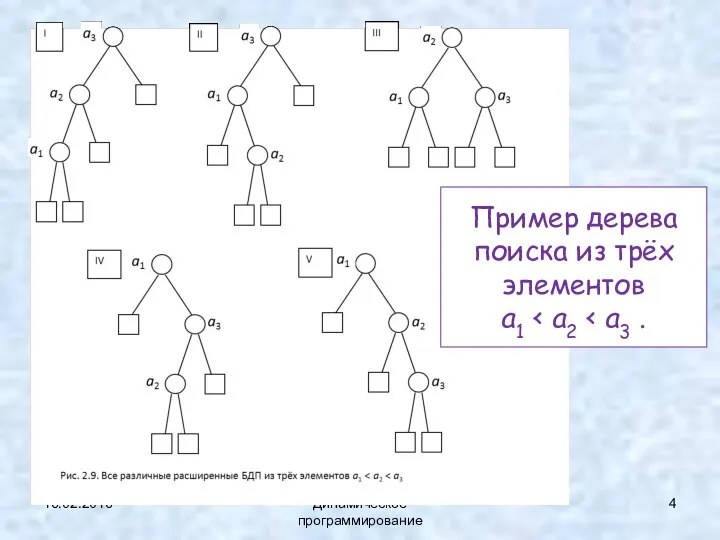
- 4. 16.02.2016 Динамическое программирование Пример дерева поиска из трёх элементов a1
- 5. Заданы вероятности предъявления элемента x для поиска: P (x = a1) = α; P (x =
- 6. Постановка задачи Поиск будет осуществляться среди набора данных a1, a2, …, an–1, an. Пусть последовательность упорядочена:
- 7. Все эти 2n + 1 событий (исходов поиска) могут быть упорядочены: B0 Заданы вероятности (или частоты)
- 8. Тогда среднее число (математическое ожидание) сравнений при поиске можно записать в виде где l (x) –
- 9. Такое дерево называют оптимальным БДП. Есть ли сходство этой задачи с задачей построения оптимального префиксного кода
- 10. Очевидное решение поставленной задачи состоит в переборе всех структурно различных бинарных деревьев с n узлами и
- 11. Конец повторения прошлой лекции 16.02.2016 Динамическое программирование
- 12. Построение оптимальных деревьев поиска Дано: набор элементов a1 набор весов Σi∈1..n pi + Σi∈0..n qi =
- 13. Пусть имеется оптимальное дерево. Согласно принципу оптимальности, лежащему в основе метода динамического программирования, левое и правое
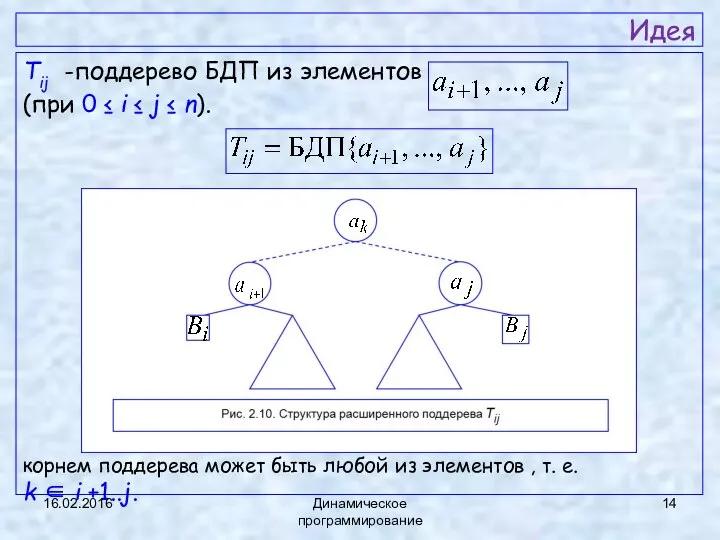
- 14. Идея Tij -поддерево БДП из элементов (при 0 ≤ i ≤ j ≤ n). корнем поддерева
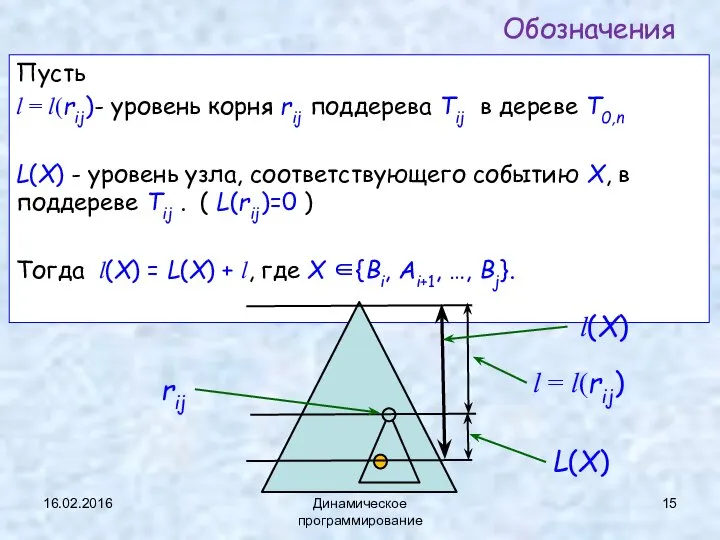
- 15. Обозначения Пусть l = l(rij)- уровень корня rij поддерева Tij в дереве T0,n L(X) - уровень
- 16. Вклад поддерева Tij в стоимость C0,n где Cij - стоимость поддерева Tij. wij - вес поддерева
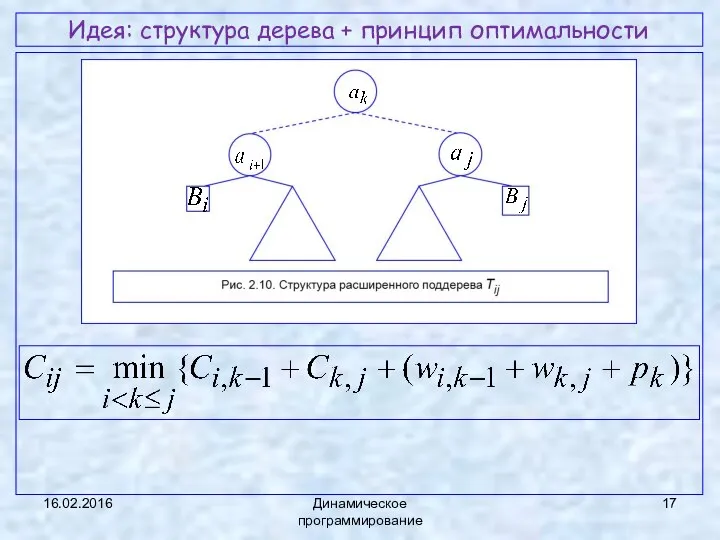
- 17. Идея: структура дерева + принцип оптимальности 16.02.2016 Динамическое программирование
- 18. Преобразование + wij не зависит от структуры поддерева Tij 16.02.2016 Динамическое программирование
- 19. Cii = 0 разности индексов k – 1 − i и j – k в слагаемых
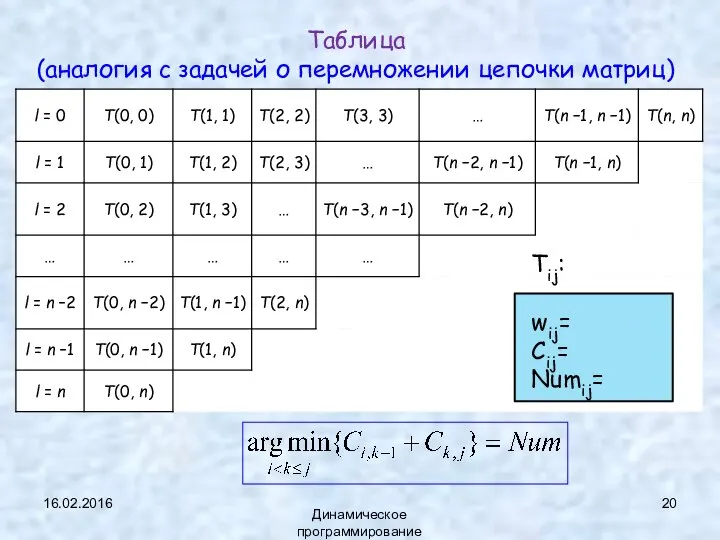
- 20. Таблица (аналогия с задачей о перемножении цепочки матриц) 16.02.2016 Динамическое программирование
- 21. for (i =0; i for (L=1; L for (i=0; i j = i + L; //
- 22. См. пример в файле «2_08_ОДП.doc» С.67,68-… 16.02.2016 Динамическое программирование
- 23. Построение БДП по таблице значений num BinT MakeOptBST (int i, j ) { int k; ElemBinT
- 24. Модификация Д.Кнута ri,j −1 ≤ rij ≤ ri +1,j 16.02.2016 Динамическое программирование Вместо k = (i
- 25. См. с.72 Так в ранее рассмотренном примере на последнем шаге при вычислении C0,4 вместо рассмотрения четырёх
- 27. Скачать презентацию



















 Продвижение сайта
Продвижение сайта Компьютерные коммуникации и интернет
Компьютерные коммуникации и интернет  AMS partner. Софты. Автоворонка в каждый Дом
AMS partner. Софты. Автоворонка в каждый Дом Обобщающий урок «Применение систем счисления» Информатика 10 класс
Обобщающий урок «Применение систем счисления» Информатика 10 класс 1D and 2D arrays
1D and 2D arrays Szkolenie techniczne 2. (Zajęcia 3)
Szkolenie techniczne 2. (Zajęcia 3) Относительные, абсолютные и смешанные ссылки
Относительные, абсолютные и смешанные ссылки Механизмы ввода и вывода
Механизмы ввода и вывода Свой канал и позиционирование
Свой канал и позиционирование Профессиональная практика в интернет-издании Петербургский дневник
Профессиональная практика в интернет-издании Петербургский дневник Розробка навчальної інформаційної системи для обчислення кількості конфігурацій, утворених складеною лінійкою
Розробка навчальної інформаційної системи для обчислення кількості конфігурацій, утворених складеною лінійкою Начала С/C++: переменная, программа и ввод-вывод. С / С++. Тема 02
Начала С/C++: переменная, программа и ввод-вывод. С / С++. Тема 02 Бронирование в системе Sabre
Бронирование в системе Sabre Облачные технологии. Традиционный способ
Облачные технологии. Традиционный способ Файлообменник
Файлообменник Информационная безопасность. Информационная безопасность. Миф или реальность?
Информационная безопасность. Информационная безопасность. Миф или реальность? Исключительные ситуации
Исключительные ситуации Информационные технологии в профессиональной деятельности
Информационные технологии в профессиональной деятельности Исторический обзор компьютерных систем хранения данных
Исторический обзор компьютерных систем хранения данных Технологии поиска и хранение информации. CУБД Access
Технологии поиска и хранение информации. CУБД Access Облачные вычисления: экономика, архитектура, основные технологии. Лекция 2
Облачные вычисления: экономика, архитектура, основные технологии. Лекция 2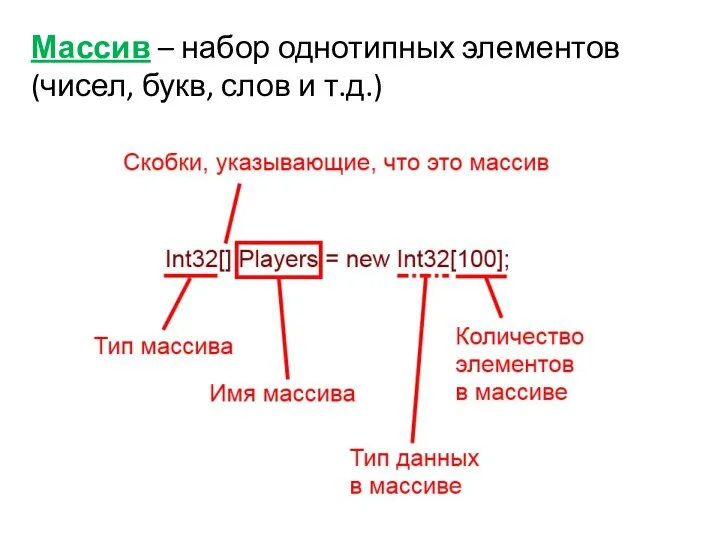 Массив. Команды для массивов
Массив. Команды для массивов История сети Интернет
История сети Интернет Використання сучасних офісних технологій в навчальному процесі
Використання сучасних офісних технологій в навчальному процесі Тест по информатике «Файл». Вариант 2. 8 класс
Тест по информатике «Файл». Вариант 2. 8 класс Виртуализация на уровне железа
Виртуализация на уровне железа Афанасий Фёдор Иван Афанасьевич Иванович Захарович Ф
Афанасий Фёдор Иван Афанасьевич Иванович Захарович Ф Программа ABBYY FineReader 10
Программа ABBYY FineReader 10