Сжатие информации. Кодирование Хаффмена.
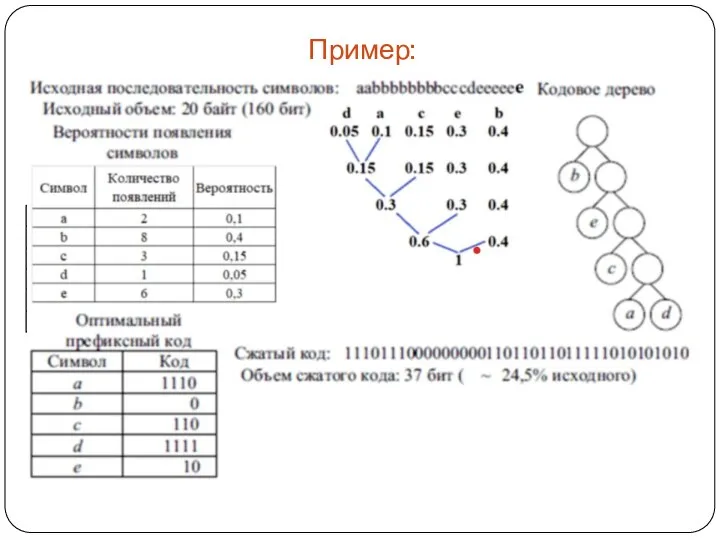
В методе Хаффмена при сжатии данных каждому символу
присваивается оптимальный префиксный код, основанный на вероятности его появления в тексте.
Префиксные коды – это коды, в которых каждое слово не является префиксом любого другого кодового слова.
Оптимальный префиксные код – это префиксный код, имеющий минимальную среднюю длину.
Алгоритм Хаффмана можно разделить на два этапа:
определение вероятности появления символов;
нахождение оптимального префиксного кода.
Находят два символа a и b с наименьшими вероятностями появления и заменяются одним фиктивным символом x , который имеет вероятность появления, равную сумме вероятностей появления символов a и b .
Используя эту процедуру рекурсивно, находится оптимальный префиксный код для меньшего множества символов.
Код для исходного множества символов получается из кодов замещающих символом путем добавления 0 или 1 перед кодом замещающего символа.
Информационная энтропия — мера неопределённости или непредсказуемости информации, неопределённость появления какого-либо символа первичного алфавита.




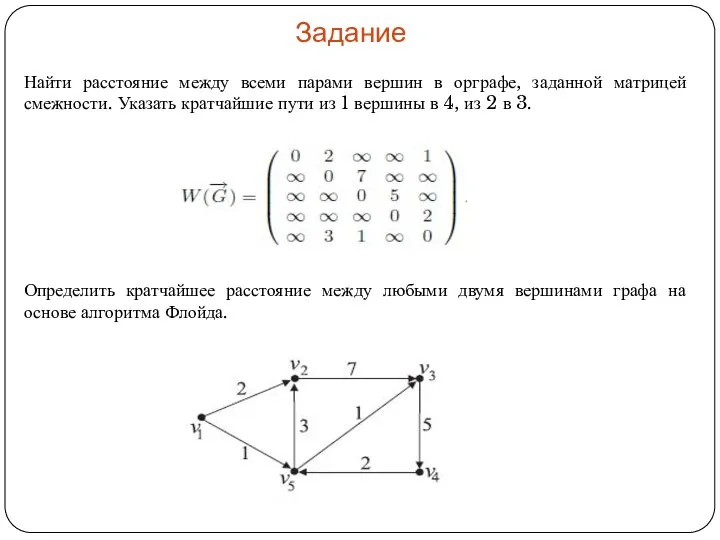

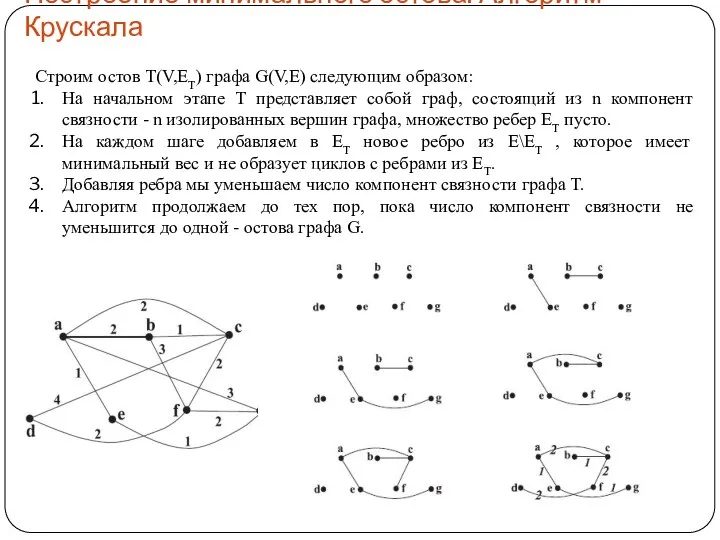

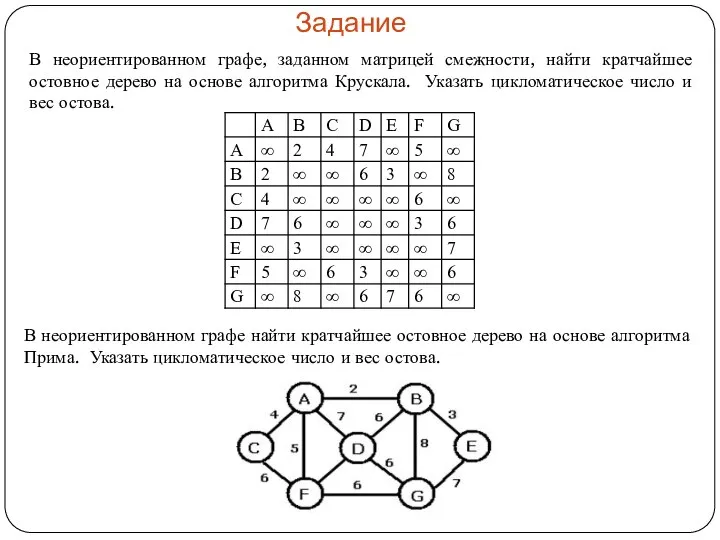

 Подготовка к ОГЭ: задача 13 (системы счисления)
Подготовка к ОГЭ: задача 13 (системы счисления) Технологии бизнес-аналитики
Технологии бизнес-аналитики Язык программирования Python. SQL 2
Язык программирования Python. SQL 2 Информационные технологии. Информатизация
Информационные технологии. Информатизация Как проверить онлайн-чек
Как проверить онлайн-чек Задания ЕГЭ. Исправление ошибок в программе
Задания ЕГЭ. Исправление ошибок в программе Мобильное приложение со смарт-контрактом
Мобильное приложение со смарт-контрактом Ғаламтормен дұрыс жұмыс жасау - мәдениет
Ғаламтормен дұрыс жұмыс жасау - мәдениет Системное ПО
Системное ПО Update on POSC xField
Update on POSC xField Introduction to Data Science
Introduction to Data Science Представление целых положительных чисел в компьютере. Разрядная сетка с фиксированной точкой
Представление целых положительных чисел в компьютере. Разрядная сетка с фиксированной точкой Типы графиков и диаграмм в электронных таблицах. Бизнес-задания
Типы графиков и диаграмм в электронных таблицах. Бизнес-задания Создание своей кисти в фотошопе
Создание своей кисти в фотошопе Claroline. E-eLearning and eWorking platform released under the GPL open-source license
Claroline. E-eLearning and eWorking platform released under the GPL open-source license ПРАВОВАЯ ОХРАНА ПРОГРАММ И ДАННЫХ. ЗАЩИТА ИНФОРМАЦИИ.
ПРАВОВАЯ ОХРАНА ПРОГРАММ И ДАННЫХ. ЗАЩИТА ИНФОРМАЦИИ.  Пример структуры данных-модели предметной области
Пример структуры данных-модели предметной области Разбор базы игрока IPshnik
Разбор базы игрока IPshnik Технологии добывания (сбора) информации
Технологии добывания (сбора) информации Как поставить электронную подпись на документ
Как поставить электронную подпись на документ Безопасность детей в сети Интернет
Безопасность детей в сети Интернет Модели и моделирование Тема 1. Модели и их типы
Модели и моделирование Тема 1. Модели и их типы Киберпреступность
Киберпреступность Elegant objects in W2MO
Elegant objects in W2MO Векторное кодирование графической информации. 6 класс
Векторное кодирование графической информации. 6 класс Экономическая информационная система
Экономическая информационная система Inversion of Control (Инверсия управления)
Inversion of Control (Инверсия управления) Задачи информатизации образования
Задачи информатизации образования