Содержание
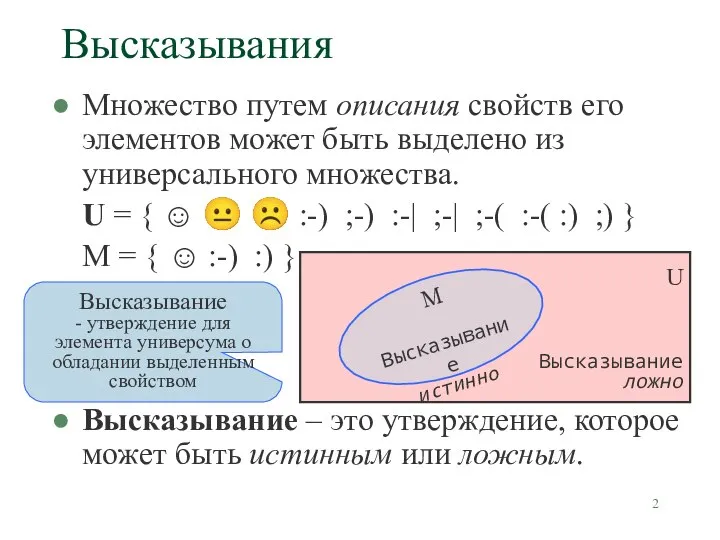
- 2. Высказывания Множество путем описания свойств его элементов может быть выделено из универсального множества. U = {
- 3. Множества истинности высказывания Подмножество универсального множества, выделенное свойством, о котором утверждается в высказывании, называют множеством истинности
- 4. Простые и составные высказывания Высказывания, которым соответствуют простые (атомарные, выделяемые одним свойством) множества истинности, называются простыми.
- 5. Логические переменные Для обозначения высказываний вводят логические переменные. Логической переменной называется такая величина х, которая может
- 6. Логические операции Связки в составных высказываниях являются логическими операциями, определенными на множестве логических переменных. Элементарные логические
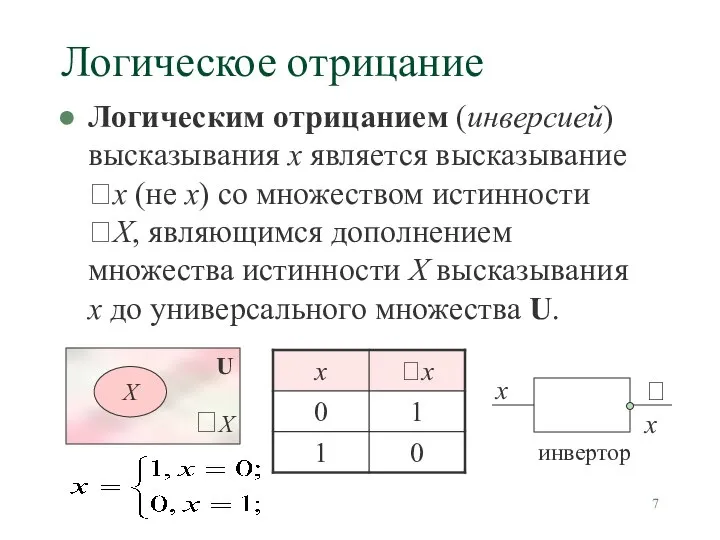
- 7. Логическое отрицание Логическим отрицанием (инверсией) высказывания х является высказывание х (не х) со множеством истинности Х,
- 8. Логическое сложение Логическим сложением (дизъюнкцией) высказываний х и у является высказывание х∨у (х или у) со
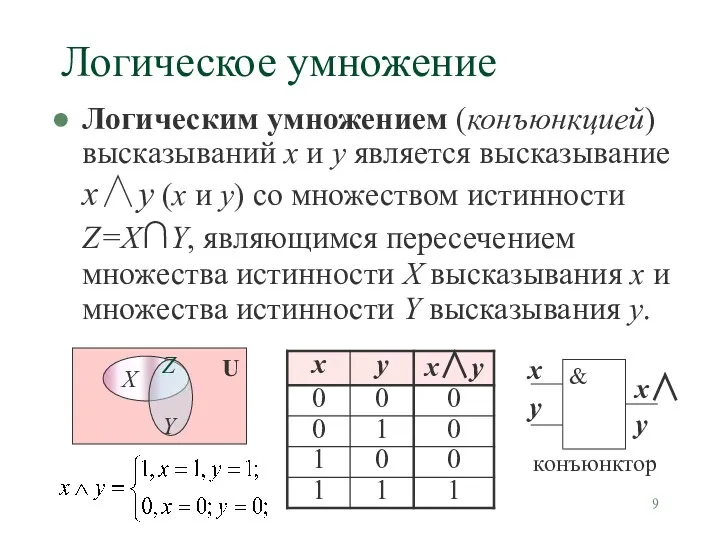
- 9. Логическое умножение Логическим умножением (конъюнкцией) высказываний х и у является высказывание х∧у (х и у) со
- 10. Алгебра высказываний (Булева Алгебра) Совокупность логических операций, определяемых на множестве логических переменных В образует «алгебру высказываний»
- 11. Формулы и порядок операций алгебры высказываний Выражения, построенные из конечного числа логических переменных, знаков логических операций
- 12. Тождественность выражений алгебры высказываний Каждая булева формула, содержащая n переменных, может рассматриваться как булева (логическая) функция
- 13. Логические функции Для обозначения сложных составных высказываний вводятся логические функции. Имея n простых высказываний x1,x2,…,xn, каждое
- 14. Способы задания логических функций Логическая функция – это функция вида f(x1,x2,…,xn), принимающая значение 0 или 1
- 15. Число различных логических функций
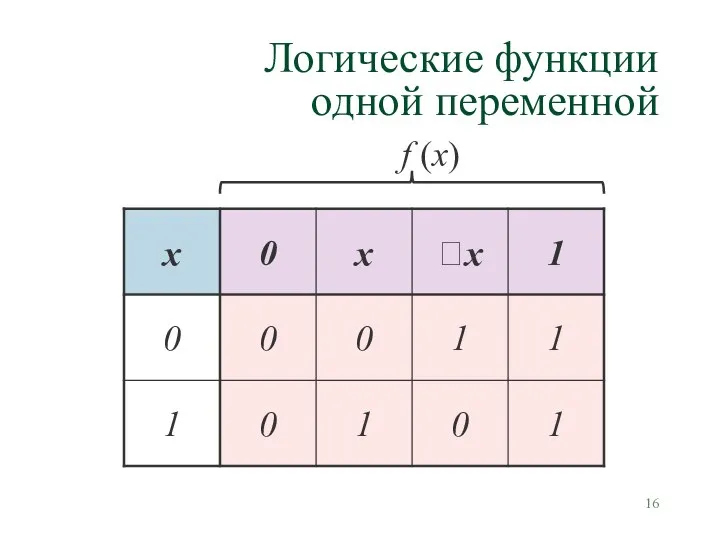
- 16. Логические функции одной переменной
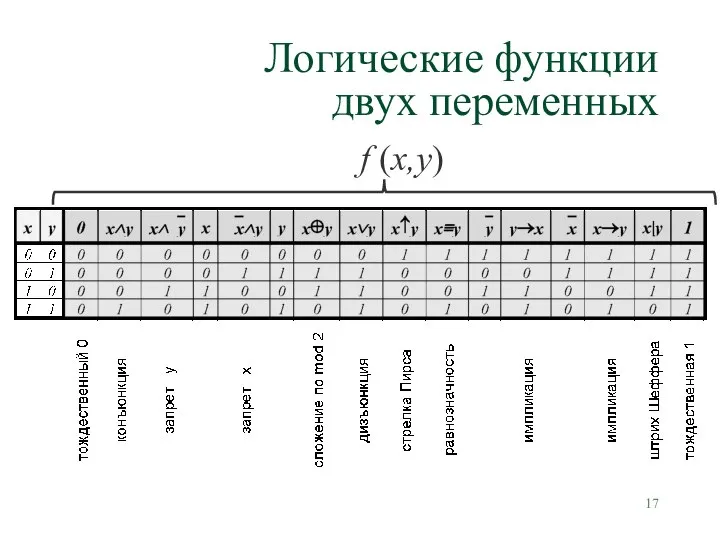
- 17. Логические функции двух переменных
- 18. Свойства элементарных функций Конъюнкция, дизъюнкция, отрицание Сложение по модулю 2 Импликация Функция Шеффера Функция Пирса Эквивалентность
- 19. Свойства конъюнкции, дизъюнкции, отрицания Аксиомы Двойное отрицание Подобные преобразования Операции с отрицанием Операции с 0 и
- 20. Свойства конъюнкции, дизъюнкции, отрицания Законы Сочетательный (свойство ассоциативности) Переместительный (свойство коммутативности) Распределительный (свойство дистрибутивности) Де Мóргана
- 21. Свойства операции сложения по модулю 2 x ⊕ y = x ⋅y +x ⋅ y =
- 22. Свойства операции сложения по модулю 2 Законы Сочетательный (свойство ассоциативности) x ⊕ ( y ⊕ z
- 23. Свойства импликации x → y =x + y Аксиомы Подобные преобразования x → х = 1
- 24. Свойства функции Шеффера x | y = Аксиомы Подобные преобразования x | х = x Операция
- 25. Свойства функции Пирса Аксиомы Подобные преобразования x ↑ х = x Операция с отрицанием x ↑x
- 26. Эквивалентность
- 27. Аналитическое представление логических функций Булевым выражением n переменных являются Элементы идентичности 0 и 1; Булевы переменные
- 28. Литералы Литерал – это булева переменная х или ее дополнение х. Литералы записывают как х1 для
- 29. Термы Терм – это выражение составленное из литералов различных переменных (по одному литералу на каждую переменную),
- 30. Минтермы Минтерм (полное произведение или конъюнктивный терм) n переменных – это булево выражение, которое имеет форму
- 31. Минтермы Теорема. Среди 2n различных минтермов для n переменных х1, х2… хn ни одна из пар
- 32. Дизъюнктивные формы представления логических функций Теорема. Любая таблично заданная, отличная от 0, логическая функция может быть
- 33. Следствие. Любая таблично заданная логическая функция может быть представлена в виде: где Доказательство: Операция, объединяющая минтермы
- 34. Объединение конъюнктивных термов переменного ранга называют нормальной дизъюнктивной формой (НДФ) представления логической функции. Например, f(x1, x2,
- 35. Объединение конъюнктивных термов максимального ранга называют совершенной нормальной дизъюнктивной формой (СНДФ) представления логической функции. Свойства СНДФ
- 36. Разложение булевой функции по m переменным Теорема. Каждая булева функция f(х1, х2… хn), отличная от 0,
- 37. Разложение булевой функции по m переменным 2. Для функции n переменных Если представить эту функцию в
- 38. Следствие 1. Если m=1, то логическая функция представляется в виде f(х1, х2… хn) = x1· f(0,
- 39. Порядок получения СНДФ по таблице истинности Процедура построения СНДФ Параметры: таблица истинности (ТИ), n – количество
- 40. Макстермы Макстерм (полная сумма или дизъюнктивный терм) n переменных – это булево выражение, которое имеет форму
- 41. Макстермы Теорема. Среди 2n различных макстермов для n переменных х1, х2… хn ни одна из пар
- 42. Конъюнктивные формы представления логических функций Теорема. Любая таблично заданная, отличная от 1, логическая функция может быть
- 43. Следствие. Любая таблично заданная логическая функция может быть представлена в виде: где Доказательство: Операция, объединяющая макстермы
- 44. Пересечение дизъюнктивных термов переменного ранга называют нормальной конъюнктивной формой (НКФ) представления логической функции. Например, f(x1, x2,
- 45. Пересечение дизъюнктивных термов максимального ранга называют совершенной нормальной конъюнктивной формой (СНКФ) представления логической функции. Свойства СНКФ
- 46. Базис представления логических функций Набор логических операций называется полным, если он позволяет представить любую логическую функцию.
- 47. Геометрическое представление логических функций Функцию 2-х переменных можно представить на плоскости в декартовой системе координат. Две
- 48. Геометрическое представление логических функций Функцию 3-х переменных можно представить в 3-мерном пространстве декартовой системы координат в
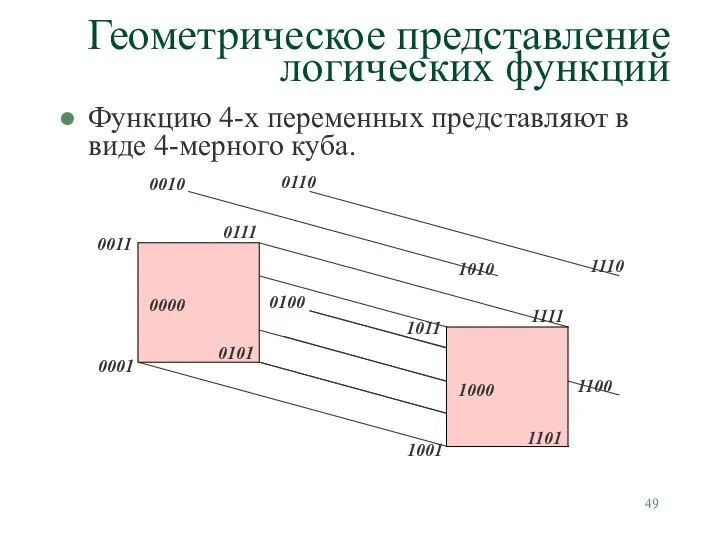
- 49. Геометрическое представление логических функций Функцию 4-х переменных представляют в виде 4-мерного куба.
- 50. Геометрическое представление логических функций Каждый набор х1, х2… хn может рассматриваться как n-мерный вектор, определяющий точку
- 51. Минимизация логических функций Форма представления логической функции, которая содержит минимальное количество термов с минимальным количеством литералов
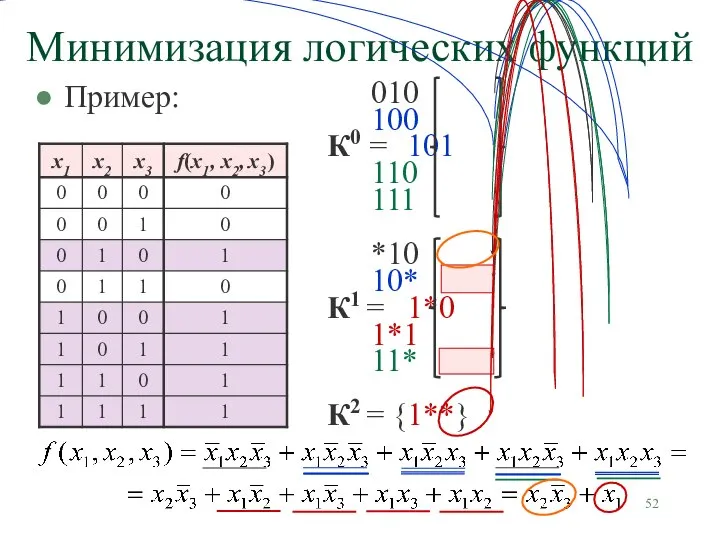
- 52. Пример: Минимизация логических функций
- 53. Пример: Минимизация логических функций
- 54. Карты Карно Карты Карно – развертки кубов на плоскости, где вершины куба – клетки карты, координаты
- 55. Правила минимизации 2 соседние клетки (2 0-куба) образуют 1-куб. Клетки, лежащие на границах карты, также являются
- 56. Минимизация функций большой размерности При числе переменных больше 4 отобразить логическую функцию в виде единой плоской
- 57. Анализ и синтез логических моделей Понятие математической модели Логические модели Виды логических моделей Задача синтеза Задача
- 58. Понятие математической модели Пусть А – произвольное множество. n-арная функция f, определенная на А со значениями
- 59. Понятие системной модели
- 60. Логические модели Логическая модель в отличии от логической функции, имея n входов, преобразует их в логические
- 61. Задачи анализа и синтеза логической модели Задача анализа логической модели (схемы) сводится к построению логической формулы,
- 62. Синтез логических моделей с одним выходом Пример: Синтезировать схему в базисе «не-импликация», если функция имеет вид
- 63. Задача синтеза модели с n входами и m выходами отличается от задачи синтеза m моделей с
- 64. Методы синтеза схем моделей Классический (основан на выделении простых импликант заданной схемы) Найти простые импликанты заданной
- 65. Временные логические функции Так как время – непрерывная величина, то вводят понятие автоматного времени, принимающего дискретные
- 66. Представление ВБФ y = f(x1,x2,…xn,t) = f0·τ0 Δ f1·τ1 Δ…Δ fs-1·τs-1, где fi – конъюнктивный/дизъюнктивный терм
- 67. Представление ВБФ. Пример
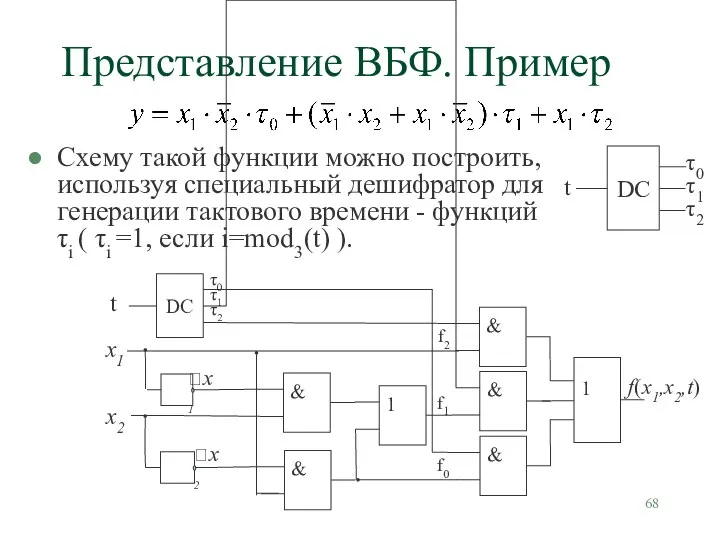
- 68. Представление ВБФ. Пример Схему такой функции можно построить, используя специальный дешифратор для генерации тактового времени -
- 69. Рекуррентные булевы функции Логическая функция, зависящая как от текущих значений входных переменных, так и от предшествующих
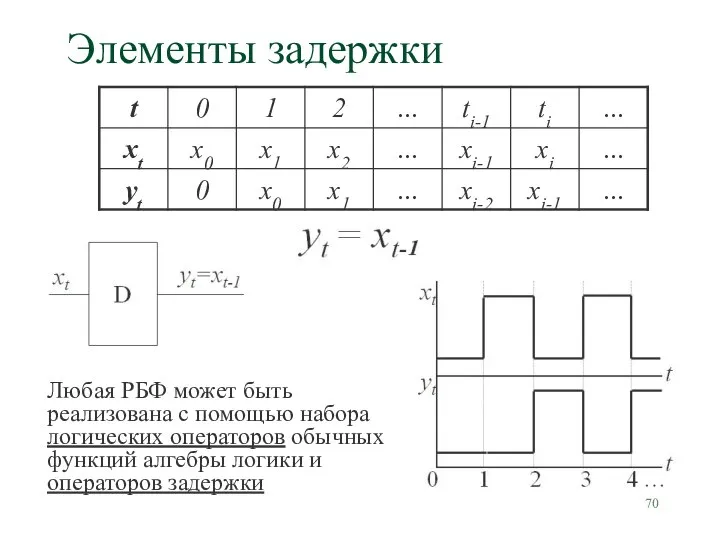
- 70. Элементы задержки Любая РБФ может быть реализована с помощью набора логических операторов обычных функций алгебры логики
- 71. Последовательные автоматы Рассмотрим частный случай РВБФ, когда на вход сигналы не подаются, а поступают только по
- 72. Последовательные автоматы
- 73. Анализ и синтез последовательных автоматов Задача анализа последовательного автомата формулируется с.о.: определить по заданной таблице состояний
- 74. Автоматы Обобщим модель последовательного автомата: F Ф Dk Xt Yt St-1 St X = { (x1,
- 76. Скачать презентацию



















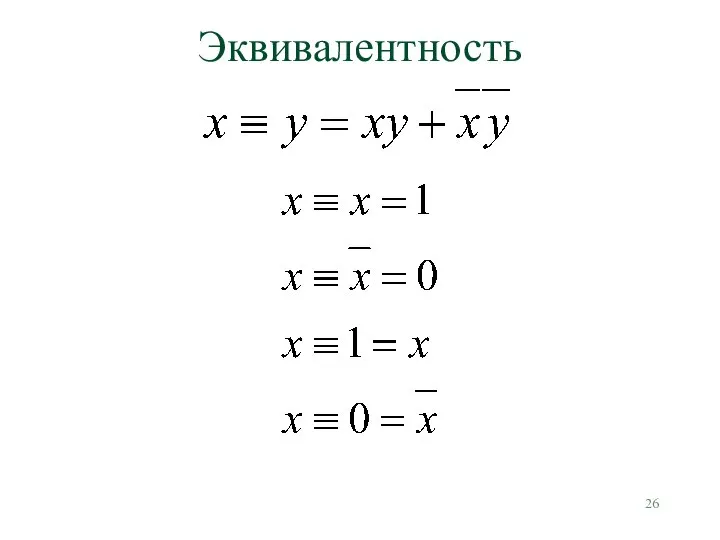












































 В гостях у пчёлки Майи (игра по теме Состав чисел первого десятка)
В гостях у пчёлки Майи (игра по теме Состав чисел первого десятка) Доминино
Доминино Сфера. Уравнение сферы
Сфера. Уравнение сферы Повторение. Линейное уравнение с одной переменной
Повторение. Линейное уравнение с одной переменной Теорема Пифагора. Пифагор и его школа
Теорема Пифагора. Пифагор и его школа Квадраттық функцияның графигін салу алгоритмі
Квадраттық функцияның графигін салу алгоритмі Презентация на тему Тригонометрические функции числового аргумента.
Презентация на тему Тригонометрические функции числового аргумента. Медианы, биссектрисы и высоты треугольника
Медианы, биссектрисы и высоты треугольника Новые мерки и умножение урок 22, с. 64-66 учебник Петерсон Л.Г.
Новые мерки и умножение урок 22, с. 64-66 учебник Петерсон Л.Г. Урок геометрии в 7 классе «Искусство рассуждать»
Урок геометрии в 7 классе «Искусство рассуждать» Boolean algebra. Logic operations. Formula and their conversion
Boolean algebra. Logic operations. Formula and their conversion Схема решения инженерной задачи
Схема решения инженерной задачи Квадратные уравнения МОУ «Москаленский лицей»
Квадратные уравнения МОУ «Москаленский лицей»  Площадь треугольника
Площадь треугольника Преобразование выражений, содержащих квадратные корни. 8 класс
Преобразование выражений, содержащих квадратные корни. 8 класс Пересечение поверхностей
Пересечение поверхностей Действия с рациональными числами (интерактивный тест) Учитель математики Бадюк Ольга Ярославна, МКОУ «Москаленский лицей»
Действия с рациональными числами (интерактивный тест) Учитель математики Бадюк Ольга Ярославна, МКОУ «Москаленский лицей» Скачать презентацию Умножение
Скачать презентацию Умножение  Презентация по математике "Интересная математика для 6 класса" - скачать бесплатно
Презентация по математике "Интересная математика для 6 класса" - скачать бесплатно Площадь криволинейной трапеции и интеграл
Площадь криволинейной трапеции и интеграл Логические задачи
Логические задачи Симплекс-метод решения задачи линейного программирования
Симплекс-метод решения задачи линейного программирования Урок математики 3 класс Умножение числа 8, умножение на 8
Урок математики 3 класс Умножение числа 8, умножение на 8 Числа Шахерезады
Числа Шахерезады Зачем мы изучаем логарифмы
Зачем мы изучаем логарифмы Решение задач по готовым чертежам. Теорема Пифагора
Решение задач по готовым чертежам. Теорема Пифагора Треугольники. Практика. Первый уровень
Треугольники. Практика. Первый уровень Исследование закона распределения погрешностей средств радиотехнических измерений
Исследование закона распределения погрешностей средств радиотехнических измерений